Model Selection for Average Reward RL with Application to Utility Maximization in Repeated Games

In standard RL, a learner attempts to learn an optimal policy for a Markov Decision Process whose structure (e.g. state space) is known. In online model selection, a learner attempts to learn an optimal policy for an MDP knowing only that it belongs to one of $M >1$ model classes of varying complexity. Recent results have shown that this can be feasibly accomplished in episodic online RL. In this work, we propose $\mathsf{MRBEAR}$, an online model selection algorithm for the average reward RL setting. The regret of the algorithm is in $\tilde O(M C_{m^*}^2 \mathsf{B}_{m^*}(T,\delta))$ where $C_{m^*}$ represents the complexity of the simplest well-specified model class and $\mathsf{B}_{m^*}(T,\delta)$ is its corresponding regret bound. This result shows that in average reward RL, like the episodic online RL, the additional cost of model selection scales only linearly in $M$, the number of model classes. We apply $\mathsf{MRBEAR}$ to the interaction between a learner and an opponent in a two-player simultaneous general-sum repeated game, where the opponent follows a fixed unknown limited memory strategy. The learner's goal is to maximize its utility without knowing the opponent's utility function. The interaction is over $T$ rounds with no episode or discounting which leads us to measure the learner's performance by average reward regret. In this application, our algorithm enjoys an opponent-complexity-dependent regret in $\tilde O(M(\mathsf{sp}(h^*) B^{m^*} A^{m^*+1})^{\frac{3}{2}} \sqrt{T})$, where $m^*\le M$ is the unknown memory limit of the opponent, $\mathsf{sp}(h^*)$ is the unknown span of optimal bias induced by the opponent, and $A$ and $B$ are the number of actions for the learner and opponent respectively. We also show that the exponential dependency on $m^*$ is inevitable by proving a lower bound on the learner's regret.

Sequential Estimation under Multiple Resources: a Bandit Point of View

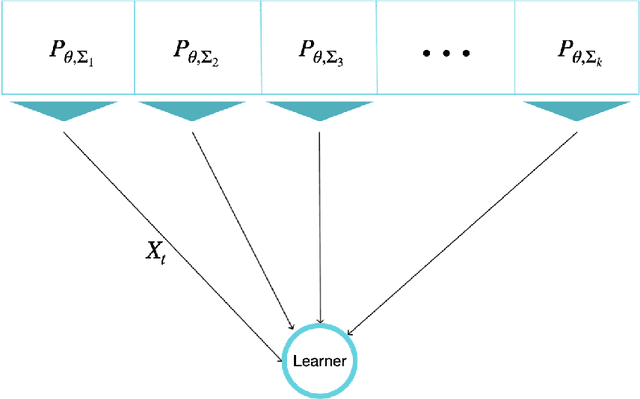
The problem of Sequential Estimation under Multiple Resources (SEMR) is defined in a federated setting. SEMR could be considered as the intersection of statistical estimation and bandit theory. In this problem, an agent is confronting with k resources to estimate a parameter $\theta$. The agent should continuously learn the quality of the resources by wisely choosing them and at the end, proposes an estimator based on the collected data. In this paper, we assume that the resources' distributions are Gaussian. The quality of the final estimator is evaluated by its mean squared error. Also, we restrict our class of estimators to unbiased estimators in order to define a meaningful notion of regret. The regret measures the performance of the agent by the variance of the final estimator in comparison to the optimal variance. We propose a lower bound to determine the fundamental limit of the setting even in the case that the distributions are not Gaussian. Also, we offer an order-optimal algorithm to achieve this lower bound.