Model Selection for Average Reward RL with Application to Utility Maximization in Repeated Games

In standard RL, a learner attempts to learn an optimal policy for a Markov Decision Process whose structure (e.g. state space) is known. In online model selection, a learner attempts to learn an optimal policy for an MDP knowing only that it belongs to one of $M >1$ model classes of varying complexity. Recent results have shown that this can be feasibly accomplished in episodic online RL. In this work, we propose $\mathsf{MRBEAR}$, an online model selection algorithm for the average reward RL setting. The regret of the algorithm is in $\tilde O(M C_{m^*}^2 \mathsf{B}_{m^*}(T,\delta))$ where $C_{m^*}$ represents the complexity of the simplest well-specified model class and $\mathsf{B}_{m^*}(T,\delta)$ is its corresponding regret bound. This result shows that in average reward RL, like the episodic online RL, the additional cost of model selection scales only linearly in $M$, the number of model classes. We apply $\mathsf{MRBEAR}$ to the interaction between a learner and an opponent in a two-player simultaneous general-sum repeated game, where the opponent follows a fixed unknown limited memory strategy. The learner's goal is to maximize its utility without knowing the opponent's utility function. The interaction is over $T$ rounds with no episode or discounting which leads us to measure the learner's performance by average reward regret. In this application, our algorithm enjoys an opponent-complexity-dependent regret in $\tilde O(M(\mathsf{sp}(h^*) B^{m^*} A^{m^*+1})^{\frac{3}{2}} \sqrt{T})$, where $m^*\le M$ is the unknown memory limit of the opponent, $\mathsf{sp}(h^*)$ is the unknown span of optimal bias induced by the opponent, and $A$ and $B$ are the number of actions for the learner and opponent respectively. We also show that the exponential dependency on $m^*$ is inevitable by proving a lower bound on the learner's regret.

Guarantees for Self-Play in Multiplayer Games via Polymatrix Decomposability

Self-play is a technique for machine learning in multi-agent systems where a learning algorithm learns by interacting with copies of itself. Self-play is useful for generating large quantities of data for learning, but has the drawback that the agents the learner will face post-training may have dramatically different behavior than the learner came to expect by interacting with itself. For the special case of two-player constant-sum games, self-play that reaches Nash equilibrium is guaranteed to produce strategies that perform well against any post-training opponent; however, no such guarantee exists for multiplayer games. We show that in games that approximately decompose into a set of two-player constant-sum games (called constant-sum polymatrix games) where global $\epsilon$-Nash equilibria are boundedly far from Nash equilibria in each subgame (called subgame stability), any no-external-regret algorithm that learns by self-play will produce a strategy with bounded vulnerability. For the first time, our results identify a structural property of multiplayer games that enable performance guarantees for the strategies produced by a broad class of self-play algorithms. We demonstrate our findings through experiments on Leduc poker.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games: Corrections

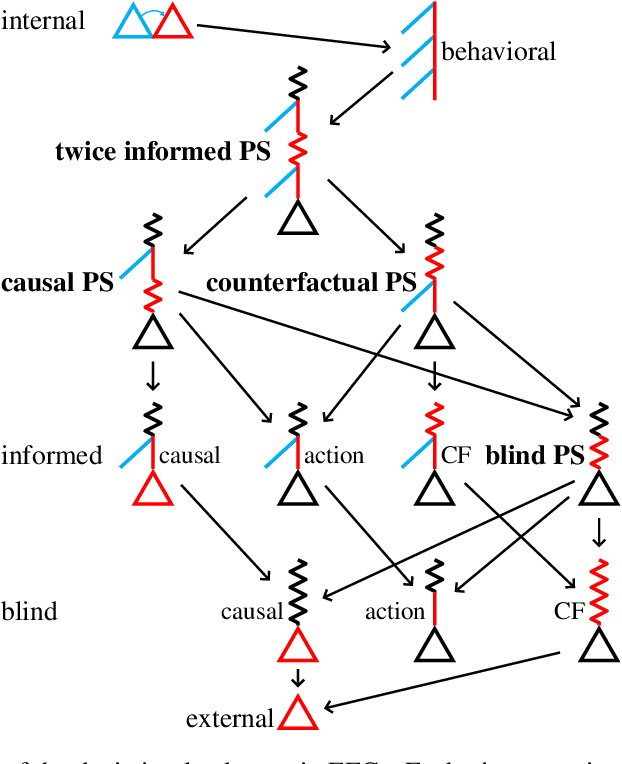
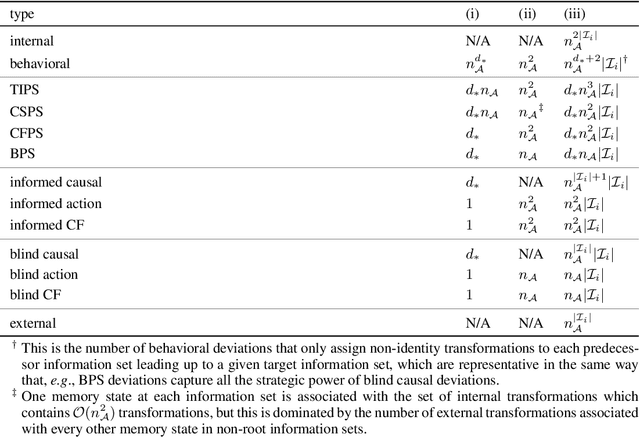
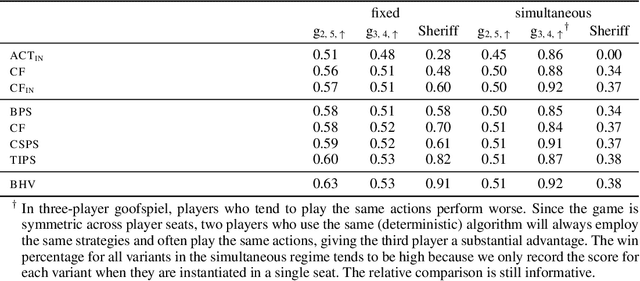
Hindsight rationality is an approach to playing general-sum games that prescribes no-regret learning dynamics for individual agents with respect to a set of deviations, and further describes jointly rational behavior among multiple agents with mediated equilibria. To develop hindsight rational learning in sequential decision-making settings, we formalize behavioral deviations as a general class of deviations that respect the structure of extensive-form games. Integrating the idea of time selection into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that achieves hindsight rationality for any given set of behavioral deviations with computation that scales closely with the complexity of the set. We identify behavioral deviation subsets, the partial sequence deviation types, that subsume previously studied types and lead to efficient EFR instances in games with moderate lengths. In addition, we present a thorough empirical analysis of EFR instantiated with different deviation types in benchmark games, where we find that stronger types typically induce better performance.

The Spotlight: A General Method for Discovering Systematic Errors in Deep Learning Models

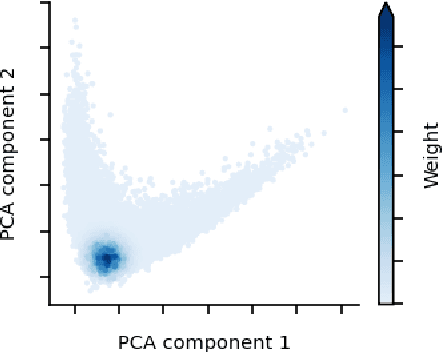
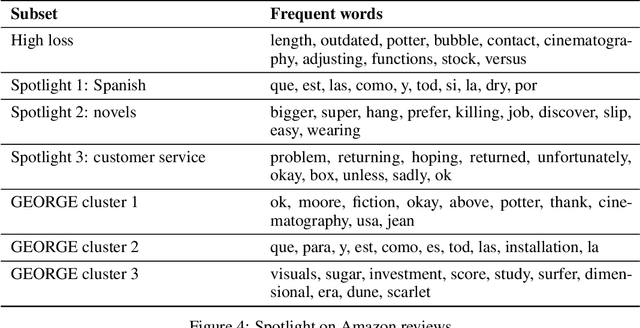
Supervised learning models often make systematic errors on rare subsets of the data. However, such systematic errors can be difficult to identify, as model performance can only be broken down across sensitive groups when these groups are known and explicitly labelled. This paper introduces a method for discovering systematic errors, which we call the spotlight. The key idea is that similar inputs tend to have similar representations in the final hidden layer of a neural network. We leverage this structure by "shining a spotlight" on this representation space to find contiguous regions where the model performs poorly. We show that the spotlight surfaces semantically meaningful areas of weakness in a wide variety of model architectures, including image classifiers, language models, and recommender systems.

Disinformation, Stochastic Harm, and Costly Filtering: A Principal-Agent Analysis of Regulating Social Media Platforms

The spread of disinformation on social media platforms such as Facebook is harmful to society. This harm can take the form of a gradual degradation of public discourse; but it can also take the form of sudden dramatic events such as the recent insurrection on Capitol Hill. The platforms themselves are in the best position to prevent the spread of disinformation, as they have the best access to relevant data and the expertise to use it. However, filtering disinformation is costly, not only for implementing filtering algorithms or employing manual filtering effort, but also because removing such highly viral content impacts user growth and thus potential advertising revenue. Since the costs of harmful content are borne by other entities, the platform will therefore have no incentive to filter at a socially-optimal level. This problem is similar to the problem of environmental regulation, in which the costs of adverse events are not directly borne by a firm, the mitigation effort of a firm is not observable, and the causal link between a harmful consequence and a specific failure is difficult to prove. In the environmental regulation domain, one solution to this issue is to perform costly monitoring to ensure that the firm takes adequate precautions according a specified rule. However, classifying disinformation is performative, and thus a fixed rule becomes less effective over time. Encoding our domain as a Markov decision process, we demonstrate that no penalty based on a static rule, no matter how large, can incentivize adequate filtering by the platform. Penalties based on an adaptive rule can incentivize optimal effort, but counterintuitively, only if the regulator sufficiently overreacts to harmful events by requiring a greater-than-optimal level of filtering.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games

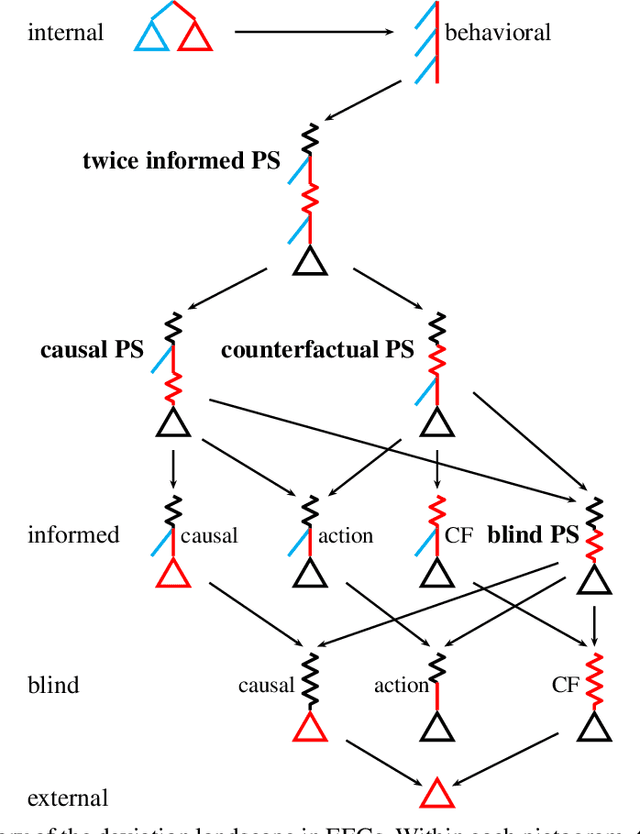
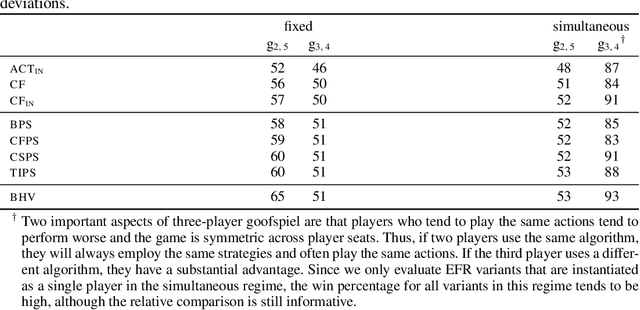
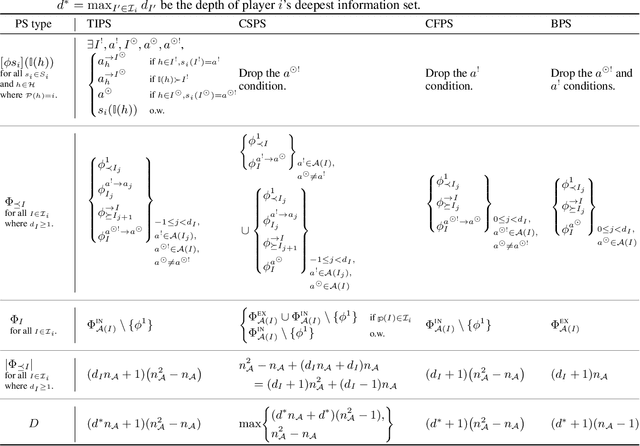
Hindsight rationality is an approach to playing multi-agent, general-sum games that prescribes no-regret learning dynamics and describes jointly rational behavior with mediated equilibria. We explore the space of deviation types in extensive-form games (EFGs) and discover powerful types that are efficient to compute in games with moderate lengths. Specifically, we identify four new types of deviations that subsume previously studied types within a broader class we call partial sequence deviations. Integrating the idea of time selection regret minimization into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that is hindsight rational for a general and natural class of deviations in EFGs. We provide instantiations and regret bounds for EFR that correspond to each partial sequence deviation type. In addition, we present a thorough empirical analysis of EFR's performance with different deviation types in common benchmark games. As theory suggests, instantiating EFR with stronger deviations leads to behavior that tends to outperform that of weaker deviations.

Hindsight and Sequential Rationality of Correlated Play

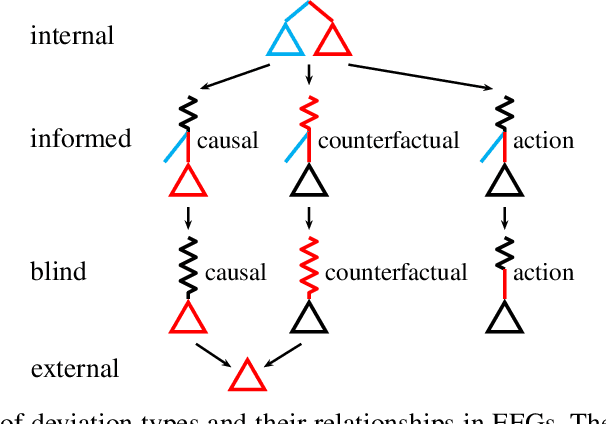
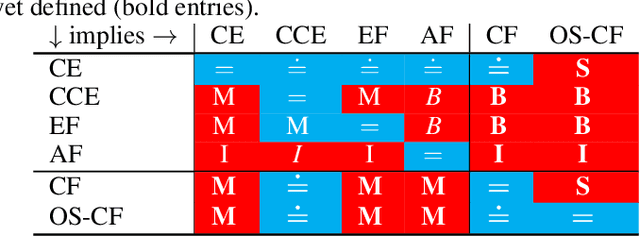
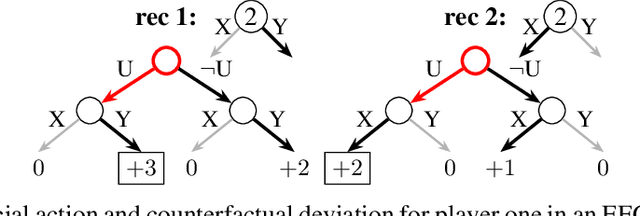
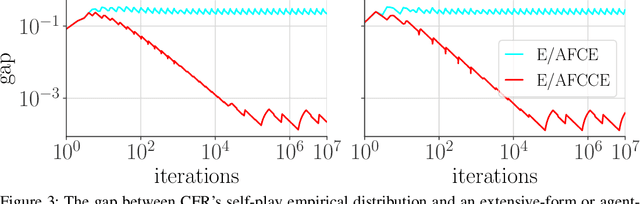
Driven by recent successes in two-player, zero-sum game solving and playing, artificial intelligence work on games has increasingly focused on algorithms that produce equilibrium-based strategies. However, this approach has been less effective at producing competent players in general-sum games or those with more than two players than in two-player, zero-sum games. An appealing alternative is to consider adaptive algorithms that ensure strong performance in hindsight relative to what could have been achieved with modified behavior. This approach also leads to a game-theoretic analysis, but in the correlated play that arises from joint learning dynamics rather than factored agent behavior at equilibrium. We develop and advocate for this hindsight rationality framing of learning in general sequential decision-making settings. To this end, we re-examine mediated equilibrium and deviation types in extensive-form games, thereby gaining a more complete understanding and resolving past misconceptions. We present a set of examples illustrating the distinct strengths and weaknesses of each type of equilibrium in the literature, and prove that no tractable concept subsumes all others. This line of inquiry culminates in the definition of the deviation and equilibrium classes that correspond to algorithms in the counterfactual regret minimization (CFR) family, relating them to all others in the literature. Examining CFR in greater detail further leads to a new recursive definition of rationality in correlated play that extends sequential rationality in a way that naturally applies to hindsight evaluation.

Alternative Function Approximation Parameterizations for Solving Games: An Analysis of $f$-Regression Counterfactual Regret Minimization

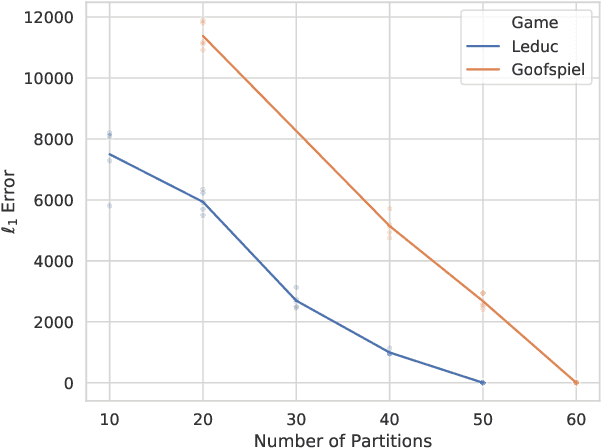
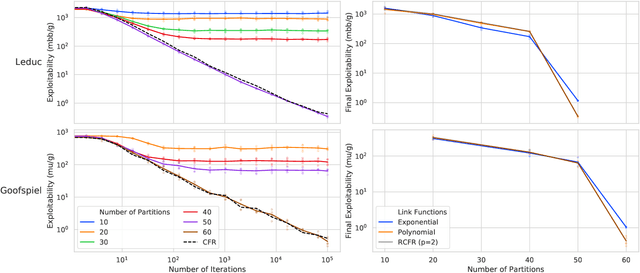
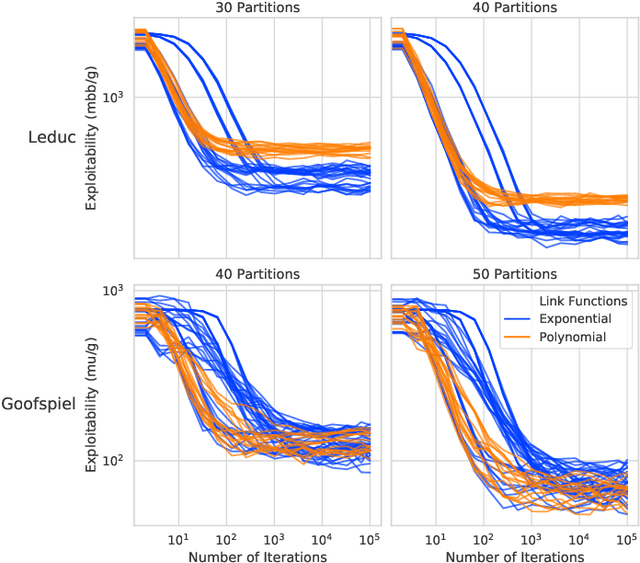
Function approximation is a powerful approach for structuring large decision problems that has facilitated great achievements in the areas of reinforcement learning and game playing. Regression counterfactual regret minimization (RCFR) is a flexible and simple algorithm for approximately solving imperfect information games with policies parameterized by a normalized rectified linear unit (ReLU). In contrast, the more conventional softmax parameterization is standard in the field of reinforcement learning and has a regret bound with a better dependence on the number of actions in the tabular case. We derive approximation error-aware regret bounds for $(\Phi, f)$-regret matching, which applies to a general class of link functions and regret objectives. These bounds recover a tighter bound for RCFR and provides a theoretical justification for RCFR implementations with alternative policy parameterizations ($f$-RCFR), including softmax. We provide exploitability bounds for $f$-RCFR with the polynomial and exponential link functions in zero-sum imperfect information games, and examine empirically how the link function interacts with the severity of the approximation to determine exploitability performance in practice. Although a ReLU parameterized policy is typically the best choice, a softmax parameterization can perform as well or better in settings that require aggressive approximation.

Bounds for Approximate Regret-Matching Algorithms

A dominant approach to solving large imperfect-information games is Counterfactural Regret Minimization (CFR). In CFR, many regret minimization problems are combined to solve the game. For very large games, abstraction is typically needed to render CFR tractable. Abstractions are often manually tuned, possibly removing important strategic differences in the full game and harming performance. Function approximation provides a natural solution to finding good abstractions to approximate the full game. A common approach to incorporating function approximation is to learn the inputs needed for a regret minimizing algorithm, allowing for generalization across many regret minimization problems. This paper gives regret bounds when a regret minimizing algorithm uses estimates instead of true values. This form of analysis is the first to generalize to a larger class of $(\Phi, f)$-regret matching algorithms, and includes different forms of regret such as swap, internal, and external regret. We demonstrate how these results give a slightly tighter bound for Regression Regret-Matching (RRM), and present a novel bound for combining regression with Hedge.