Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games: Corrections

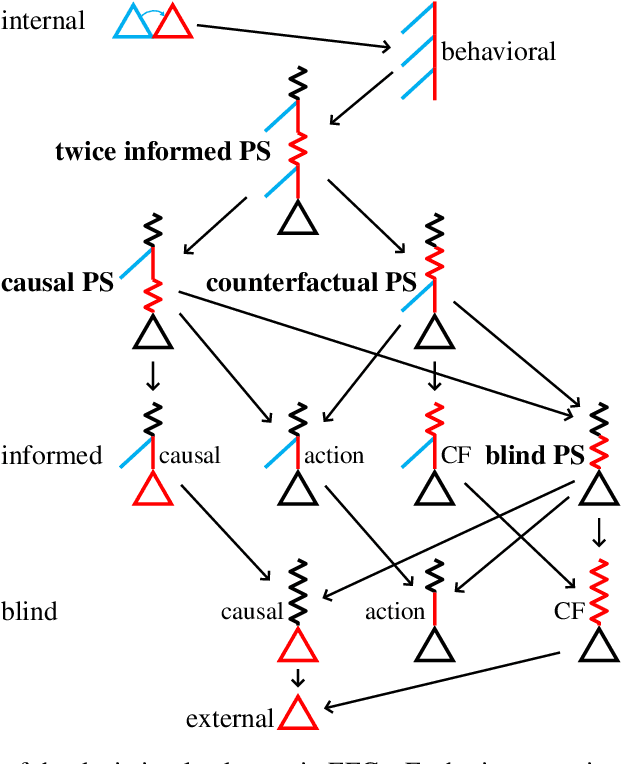
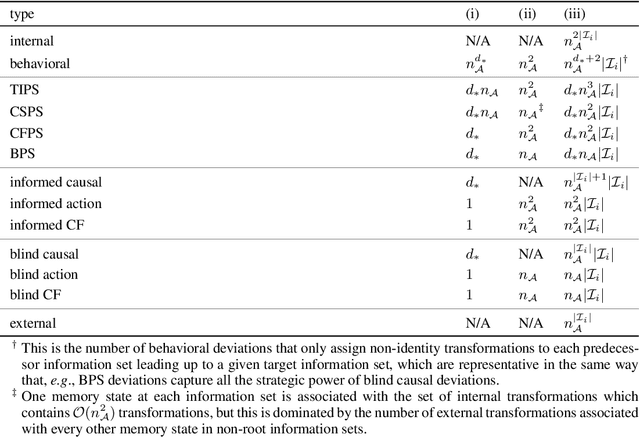
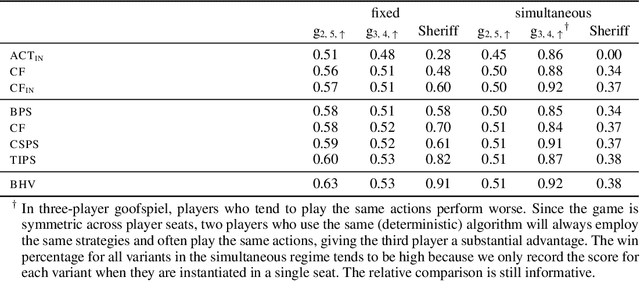
Hindsight rationality is an approach to playing general-sum games that prescribes no-regret learning dynamics for individual agents with respect to a set of deviations, and further describes jointly rational behavior among multiple agents with mediated equilibria. To develop hindsight rational learning in sequential decision-making settings, we formalize behavioral deviations as a general class of deviations that respect the structure of extensive-form games. Integrating the idea of time selection into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that achieves hindsight rationality for any given set of behavioral deviations with computation that scales closely with the complexity of the set. We identify behavioral deviation subsets, the partial sequence deviation types, that subsume previously studied types and lead to efficient EFR instances in games with moderate lengths. In addition, we present a thorough empirical analysis of EFR instantiated with different deviation types in benchmark games, where we find that stronger types typically induce better performance.

The Partially Observable History Process

We introduce the partially observable history process (POHP) formalism for reinforcement learning. POHP centers around the actions and observations of a single agent and abstracts away the presence of other players without reducing them to stochastic processes. Our formalism provides a streamlined interface for designing algorithms that defy categorization as exclusively single or multi-agent, and for developing theory that applies across these domains. We show how the POHP formalism unifies traditional models including the Markov decision process, the Markov game, the extensive-form game, and their partially observable extensions, without introducing burdensome technical machinery or violating the philosophical underpinnings of reinforcement learning. We illustrate the utility of our formalism by concisely exploring observable sequential rationality, re-deriving the extensive-form regret minimization (EFR) algorithm, and examining EFR's theoretical properties in greater generality.