Christopher Solinas
Approximating Nash Equilibria in General-Sum Games via Meta-Learning
Apr 26, 2025Abstract:Nash equilibrium is perhaps the best-known solution concept in game theory. Such a solution assigns a strategy to each player which offers no incentive to unilaterally deviate. While a Nash equilibrium is guaranteed to always exist, the problem of finding one in general-sum games is PPAD-complete, generally considered intractable. Regret minimization is an efficient framework for approximating Nash equilibria in two-player zero-sum games. However, in general-sum games, such algorithms are only guaranteed to converge to a coarse-correlated equilibrium (CCE), a solution concept where players can correlate their strategies. In this work, we use meta-learning to minimize the correlations in strategies produced by a regret minimizer. This encourages the regret minimizer to find strategies that are closer to a Nash equilibrium. The meta-learned regret minimizer is still guaranteed to converge to a CCE, but we give a bound on the distance to Nash equilibrium in terms of our meta-loss. We evaluate our approach in general-sum imperfect information games. Our algorithms provide significantly better approximations of Nash equilibria than state-of-the-art regret minimization techniques.
Transformer Based Planning in the Observation Space with Applications to Trick Taking Card Games
Apr 19, 2024Abstract:Traditional search algorithms have issues when applied to games of imperfect information where the number of possible underlying states and trajectories are very large. This challenge is particularly evident in trick-taking card games. While state sampling techniques such as Perfect Information Monte Carlo (PIMC) search has shown success in these contexts, they still have major limitations. We present Generative Observation Monte Carlo Tree Search (GO-MCTS), which utilizes MCTS on observation sequences generated by a game specific model. This method performs the search within the observation space and advances the search using a model that depends solely on the agent's observations. Additionally, we demonstrate that transformers are well-suited as the generative model in this context, and we demonstrate a process for iteratively training the transformer via population-based self-play. The efficacy of GO-MCTS is demonstrated in various games of imperfect information, such as Hearts, Skat, and "The Crew: The Quest for Planet Nine," with promising results.
History Filtering in Imperfect Information Games: Algorithms and Complexity
Nov 24, 2023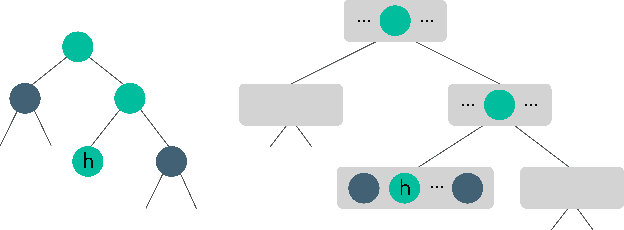
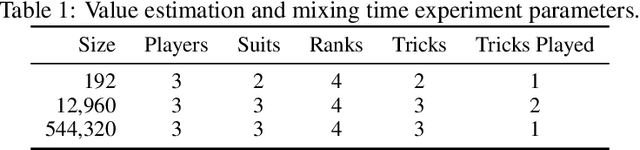
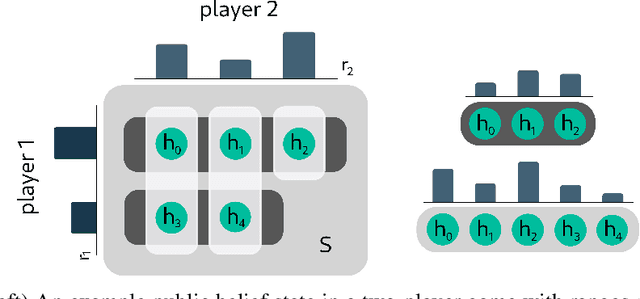

Abstract:Historically applied exclusively to perfect information games, depth-limited search with value functions has been key to recent advances in AI for imperfect information games. Most prominent approaches with strong theoretical guarantees require subgame decomposition - a process in which a subgame is computed from public information and player beliefs. However, subgame decomposition can itself require non-trivial computations, and its tractability depends on the existence of efficient algorithms for either full enumeration or generation of the histories that form the root of the subgame. Despite this, no formal analysis of the tractability of such computations has been established in prior work, and application domains have often consisted of games, such as poker, for which enumeration is trivial on modern hardware. Applying these ideas to more complex domains requires understanding their cost. In this work, we introduce and analyze the computational aspects and tractability of filtering histories for subgame decomposition. We show that constructing a single history from the root of the subgame is generally intractable, and then provide a necessary and sufficient condition for efficient enumeration. We also introduce a novel Markov Chain Monte Carlo-based generation algorithm for trick-taking card games - a domain where enumeration is often prohibitively expensive. Our experiments demonstrate its improved scalability in the trick-taking card game Oh Hell. These contributions clarify when and how depth-limited search via subgame decomposition can be an effective tool for sequential decision-making in imperfect information settings.
Policy Based Inference in Trick-Taking Card Games
May 27, 2019


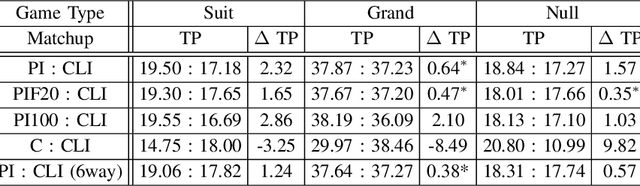
Abstract:Trick-taking card games feature a large amount of private information that slowly gets revealed through a long sequence of actions. This makes the number of histories exponentially large in the action sequence length, as well as creating extremely large information sets. As a result, these games become too large to solve. To deal with these issues many algorithms employ inference, the estimation of the probability of states within an information set. In this paper, we demonstrate a Policy Based Inference (PI) algorithm that uses player modelling to infer the probability we are in a given state. We perform experiments in the German trick-taking card game Skat, in which we show that this method vastly improves the inference as compared to previous work, and increases the performance of the state-of-the-art Skat AI system Kermit when it is employed into its determinized search algorithm.
Learning Policies from Human Data for Skat
May 27, 2019



Abstract:Decision-making in large imperfect information games is difficult. Thanks to recent success in Poker, Counterfactual Regret Minimization (CFR) methods have been at the forefront of research in these games. However, most of the success in large games comes with the use of a forward model and powerful state abstractions. In trick-taking card games like Bridge or Skat, large information sets and an inability to advance the simulation without fully determinizing the state make forward search problematic. Furthermore, state abstractions can be especially difficult to construct because the precise holdings of each player directly impact move values. In this paper we explore learning model-free policies for Skat from human game data using deep neural networks (DNN). We produce a new state-of-the-art system for bidding and game declaration by introducing methods to a) directly vary the aggressiveness of the bidder and b) declare games based on expected value while mitigating issues with rarely observed state-action pairs. Although cardplay policies learned through imitation are slightly weaker than the current best search-based method, they run orders of magnitude faster. We also explore how these policies could be learned directly from experience in a reinforcement learning setting and discuss the value of incorporating human data for this task.
Improving Search with Supervised Learning in Trick-Based Card Games
Mar 22, 2019



Abstract:In trick-taking card games, a two-step process of state sampling and evaluation is widely used to approximate move values. While the evaluation component is vital, the accuracy of move value estimates is also fundamentally linked to how well the sampling distribution corresponds the true distribution. Despite this, recent work in trick-taking card game AI has mainly focused on improving evaluation algorithms with limited work on improving sampling. In this paper, we focus on the effect of sampling on the strength of a player and propose a novel method of sampling more realistic states given move history. In particular, we use predictions about locations of individual cards made by a deep neural network --- trained on data from human gameplay - in order to sample likely worlds for evaluation. This technique, used in conjunction with Perfect Information Monte Carlo (PIMC) search, provides a substantial increase in cardplay strength in the popular trick-taking card game of Skat.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge