History Filtering in Imperfect Information Games: Algorithms and Complexity
Paper and Code
Nov 24, 2023
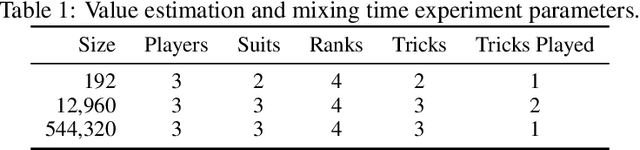
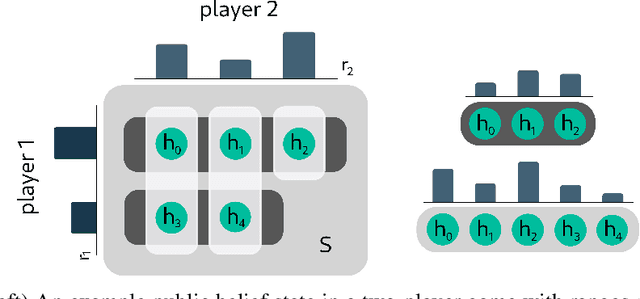

Historically applied exclusively to perfect information games, depth-limited search with value functions has been key to recent advances in AI for imperfect information games. Most prominent approaches with strong theoretical guarantees require subgame decomposition - a process in which a subgame is computed from public information and player beliefs. However, subgame decomposition can itself require non-trivial computations, and its tractability depends on the existence of efficient algorithms for either full enumeration or generation of the histories that form the root of the subgame. Despite this, no formal analysis of the tractability of such computations has been established in prior work, and application domains have often consisted of games, such as poker, for which enumeration is trivial on modern hardware. Applying these ideas to more complex domains requires understanding their cost. In this work, we introduce and analyze the computational aspects and tractability of filtering histories for subgame decomposition. We show that constructing a single history from the root of the subgame is generally intractable, and then provide a necessary and sufficient condition for efficient enumeration. We also introduce a novel Markov Chain Monte Carlo-based generation algorithm for trick-taking card games - a domain where enumeration is often prohibitively expensive. Our experiments demonstrate its improved scalability in the trick-taking card game Oh Hell. These contributions clarify when and how depth-limited search via subgame decomposition can be an effective tool for sequential decision-making in imperfect information settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge