Learning Admissible Heuristics for A*: Theory and Practice

Heuristic functions are central to the performance of search algorithms such as A-star, where admissibility - the property of never overestimating the true shortest-path cost - guarantees solution optimality. Recent deep learning approaches often disregard admissibility and provide limited guarantees on generalization beyond the training data. This paper addresses both of these limitations. First, we pose heuristic learning as a constrained optimization problem and introduce Cross-Entropy Admissibility (CEA), a loss function that enforces admissibility during training. On the Rubik's Cube domain, this method yields near-admissible heuristics with significantly stronger guidance than compressed pattern database (PDB) heuristics. Theoretically, we study the sample complexity of learning heuristics. By leveraging PDB abstractions and the structural properties of graphs such as the Rubik's Cube, we tighten the bound on the number of training samples needed for A-star to generalize. Replacing a general hypothesis class with a ReLU neural network gives bounds that depend primarily on the network's width and depth, rather than on graph size. Using the same network, we also provide the first generalization guarantees for goal-dependent heuristics.

Online Submission and Evaluation System Design for Competition Operations

Research communities have developed benchmark datasets across domains to compare the performance of algorithms and techniques However, tracking the progress in these research areas is not easy, as publications appear in different venues at the same time, and many of them claim to represent the state-of-the-art. To address this, research communities often organise periodic competitions to evaluate the performance of various algorithms and techniques, thereby tracking advancements in the field. However, these competitions pose a significant operational burden. The organisers must manage and evaluate a large volume of submissions. Furthermore, participants typically develop their solutions in diverse environments, leading to compatibility issues during the evaluation of their submissions. This paper presents an online competition system that automates the submission and evaluation process for a competition. The competition system allows organisers to manage large numbers of submissions efficiently, utilising isolated environments to evaluate submissions. This system has already been used successfully for several competitions, including the Grid-Based Pathfinding Competition and the League of Robot Runners competition.

A Parallel CPU-GPU Framework for Cost-Bounded DFS with Applications to IDA* and BTS

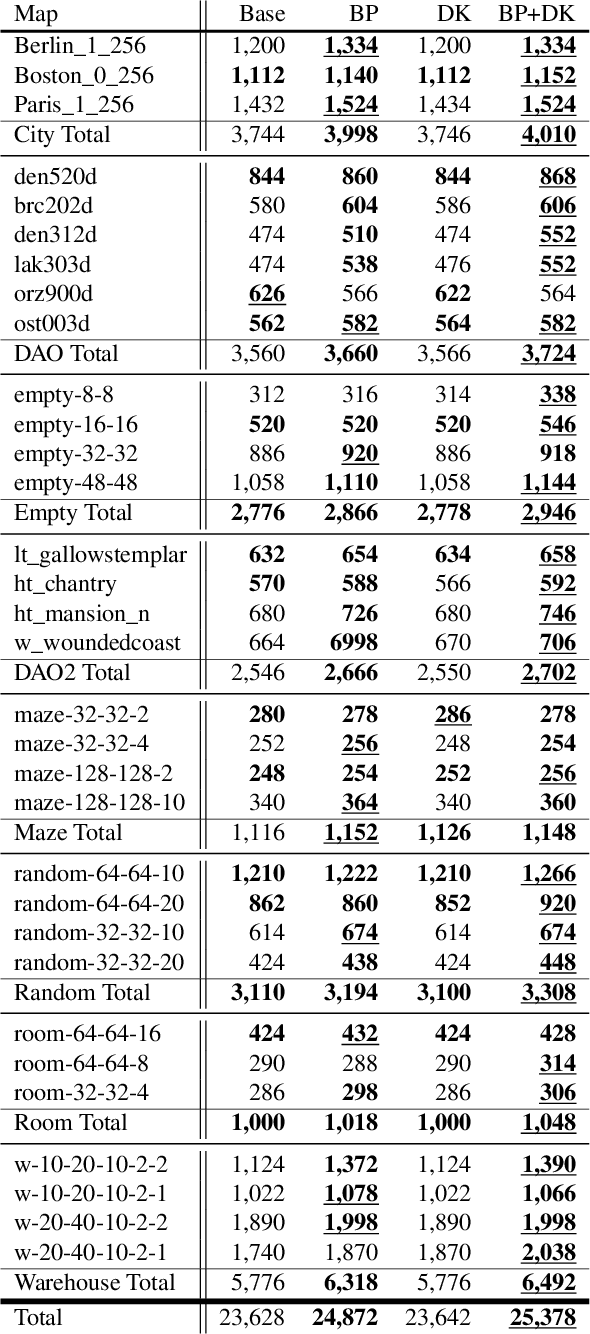
The rapid advancement of GPU technology has unlocked powerful parallel processing capabilities, creating new opportunities to enhance classic search algorithms. A recent successful application of GPUs is in compressing large pattern database (PDB) heuristics using neural networks while preserving heuristic admissibility. However, very few algorithms have been designed to exploit GPUs during search. Several variants of A* exist that batch GPU computations. In this paper we introduce a method for batching GPU computations in depth first search. In particular, we describe a new cost-bounded depth-first search (CB-DFS) method that leverages the combined parallelism of modern CPUs and GPUs. This is used to create algorithms like \emph{Batch IDA*}, an extension of the Iterative Deepening A* (IDA*) algorithm, or Batch BTS, an extensions of Budgeted Tree Search. Our approach builds on the general approach used by Asynchronous Parallel IDA* (AIDA*), while maintaining optimality guarantees. We evaluate the approach on the 3x3 Rubik's Cube and 4x4 sliding tile puzzle (STP), showing that GPU operations can be efficiently batched in DFS. Additionally, we conduct extensive experiments to analyze the effects of hyperparameters, neural network heuristic size, and hardware resources on performance.

Approximating Nash Equilibria in General-Sum Games via Meta-Learning

Nash equilibrium is perhaps the best-known solution concept in game theory. Such a solution assigns a strategy to each player which offers no incentive to unilaterally deviate. While a Nash equilibrium is guaranteed to always exist, the problem of finding one in general-sum games is PPAD-complete, generally considered intractable. Regret minimization is an efficient framework for approximating Nash equilibria in two-player zero-sum games. However, in general-sum games, such algorithms are only guaranteed to converge to a coarse-correlated equilibrium (CCE), a solution concept where players can correlate their strategies. In this work, we use meta-learning to minimize the correlations in strategies produced by a regret minimizer. This encourages the regret minimizer to find strategies that are closer to a Nash equilibrium. The meta-learned regret minimizer is still guaranteed to converge to a CCE, but we give a bound on the distance to Nash equilibrium in terms of our meta-loss. We evaluate our approach in general-sum imperfect information games. Our algorithms provide significantly better approximations of Nash equilibria than state-of-the-art regret minimization techniques.

Parallelizing Multi-objective A* Search

The Multi-objective Shortest Path (MOSP) problem is a classic network optimization problem that aims to find all Pareto-optimal paths between two points in a graph with multiple edge costs. Recent studies on multi-objective search with A* (MOA*) have demonstrated superior performance in solving difficult MOSP instances. This paper presents a novel search framework that allows efficient parallelization of MOA* with different objective orders. The framework incorporates a unique upper bounding strategy that helps the search reduce the problem's dimensionality to one in certain cases. Experimental results demonstrate that the proposed framework can enhance the performance of recent A*-based solutions, with the speed-up proportional to the problem dimension.

On Parallel External-Memory Bidirectional Search

Parallelization and External Memory (PEM) techniques have significantly enhanced the capabilities of search algorithms when solving large-scale problems. Previous research on PEM has primarily centered on unidirectional algorithms, with only one publication on bidirectional PEM that focuses on the meet-in-the-middle (MM) algorithm. Building upon this foundation, this paper presents a framework that integrates both uni- and bi-directional best-first search algorithms into this framework. We then develop a PEM variant of the state-of-the-art bidirectional heuristic search (\BiHS) algorithm BAE* (PEM-BAE*). As previous work on \BiHS did not focus on scaling problem sizes, this work enables us to evaluate bidirectional algorithms on hard problems. Empirical evaluation shows that PEM-BAE* outperforms the PEM variants of A* and the MM algorithm, as well as a parallel variant of IDA*. These findings mark a significant milestone, revealing that bidirectional search algorithms clearly outperform unidirectional search algorithms across several domains, even when equipped with state-of-the-art heuristics.

Set-Based Retrograde Analysis: Precomputing the Solution to 24-card Bridge Double Dummy Deals

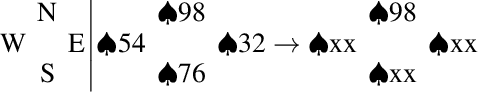
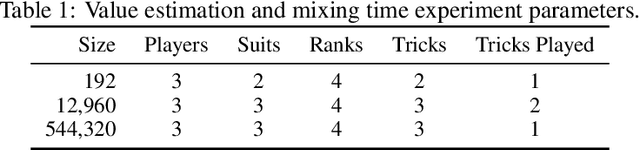
Retrograde analysis is used in game-playing programs to solve states at the end of a game, working backwards toward the start of the game. The algorithm iterates through and computes the perfect-play value for as many states as resources allow. We introduce setrograde analysis which achieves the same results by operating on sets of states that have the same game value. The algorithm is demonstrated by computing exact solutions for Bridge double dummy card-play. For deals with 24 cards remaining to be played ($10^{27}$ states, which can be reduced to $10^{15}$ states using preexisting techniques), we strongly solve all deals. The setrograde algorithm performs a factor of $10^3$ fewer search operations than a standard retrograde algorithm, producing a database with a factor of $10^4$ fewer entries. For applicable domains, this allows retrograde searching to reach unprecedented search depths.

Transformer Based Planning in the Observation Space with Applications to Trick Taking Card Games

Traditional search algorithms have issues when applied to games of imperfect information where the number of possible underlying states and trajectories are very large. This challenge is particularly evident in trick-taking card games. While state sampling techniques such as Perfect Information Monte Carlo (PIMC) search has shown success in these contexts, they still have major limitations. We present Generative Observation Monte Carlo Tree Search (GO-MCTS), which utilizes MCTS on observation sequences generated by a game specific model. This method performs the search within the observation space and advances the search using a model that depends solely on the agent's observations. Additionally, we demonstrate that transformers are well-suited as the generative model in this context, and we demonstrate a process for iteratively training the transformer via population-based self-play. The efficacy of GO-MCTS is demonstrated in various games of imperfect information, such as Hearts, Skat, and "The Crew: The Quest for Planet Nine," with promising results.

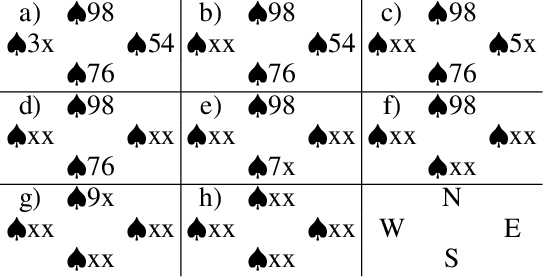
Clique Analysis and Bypassing in Continuous-Time Conflict-Based Search

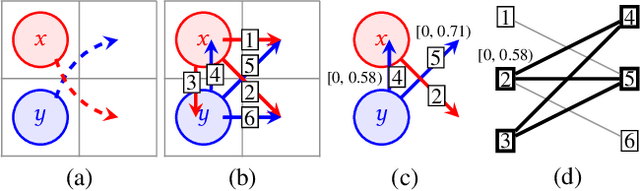
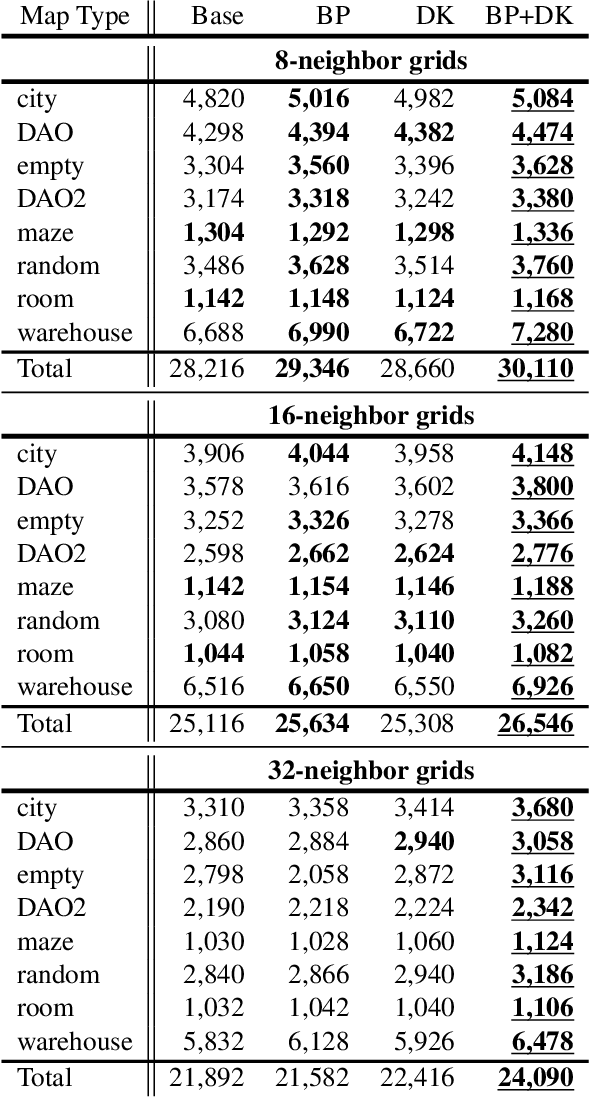
While the study of unit-cost Multi-Agent Pathfinding (MAPF) problems has been popular, many real-world problems require continuous time and costs due to various movement models. In this context, this paper studies symmetry-breaking enhancements for Continuous-Time Conflict-Based Search (CCBS), a solver for continuous-time MAPF. Resolving conflict symmetries in MAPF can require an exponential amount of work. We adapt known enhancements from unit-cost domains for CCBS: bypassing, which resolves cost symmetries and biclique constraints which resolve spatial conflict symmetries. We formulate a novel combination of biclique constraints with disjoint splitting for spatial conflict symmetries. Finally, we show empirically that these enhancements yield a statistically significant performance improvement versus previous state of the art, solving problems for up to 10% or 20% more agents in the same amount of time on dense graphs.

History Filtering in Imperfect Information Games: Algorithms and Complexity

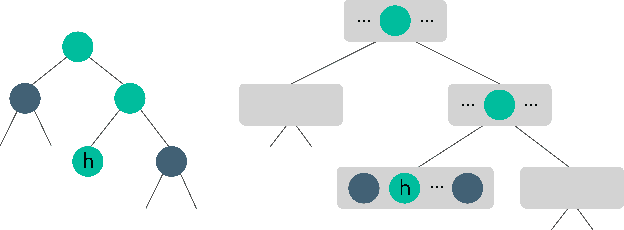
Historically applied exclusively to perfect information games, depth-limited search with value functions has been key to recent advances in AI for imperfect information games. Most prominent approaches with strong theoretical guarantees require subgame decomposition - a process in which a subgame is computed from public information and player beliefs. However, subgame decomposition can itself require non-trivial computations, and its tractability depends on the existence of efficient algorithms for either full enumeration or generation of the histories that form the root of the subgame. Despite this, no formal analysis of the tractability of such computations has been established in prior work, and application domains have often consisted of games, such as poker, for which enumeration is trivial on modern hardware. Applying these ideas to more complex domains requires understanding their cost. In this work, we introduce and analyze the computational aspects and tractability of filtering histories for subgame decomposition. We show that constructing a single history from the root of the subgame is generally intractable, and then provide a necessary and sufficient condition for efficient enumeration. We also introduce a novel Markov Chain Monte Carlo-based generation algorithm for trick-taking card games - a domain where enumeration is often prohibitively expensive. Our experiments demonstrate its improved scalability in the trick-taking card game Oh Hell. These contributions clarify when and how depth-limited search via subgame decomposition can be an effective tool for sequential decision-making in imperfect information settings.