Set-Based Retrograde Analysis: Precomputing the Solution to 24-card Bridge Double Dummy Deals

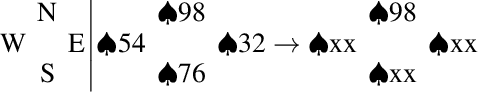
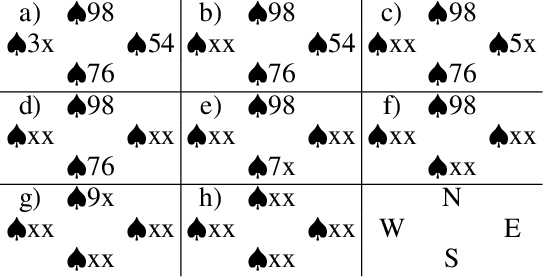
Retrograde analysis is used in game-playing programs to solve states at the end of a game, working backwards toward the start of the game. The algorithm iterates through and computes the perfect-play value for as many states as resources allow. We introduce setrograde analysis which achieves the same results by operating on sets of states that have the same game value. The algorithm is demonstrated by computing exact solutions for Bridge double dummy card-play. For deals with 24 cards remaining to be played ($10^{27}$ states, which can be reduced to $10^{15}$ states using preexisting techniques), we strongly solve all deals. The setrograde algorithm performs a factor of $10^3$ fewer search operations than a standard retrograde algorithm, producing a database with a factor of $10^4$ fewer entries. For applicable domains, this allows retrograde searching to reach unprecedented search depths.

Best-First and Depth-First Minimax Search in Practice

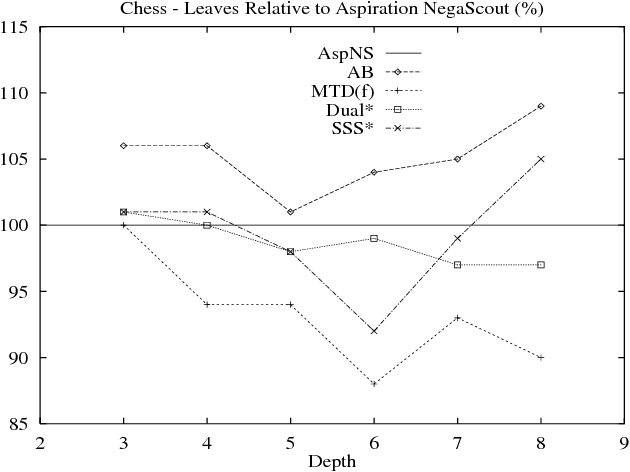
Most practitioners use a variant of the Alpha-Beta algorithm, a simple depth-first pro- cedure, for searching minimax trees. SSS*, with its best-first search strategy, reportedly offers the potential for more efficient search. However, the complex formulation of the al- gorithm and its alleged excessive memory requirements preclude its use in practice. For two decades, the search efficiency of "smart" best-first SSS* has cast doubt on the effectiveness of "dumb" depth-first Alpha-Beta. This paper presents a simple framework for calling Alpha-Beta that allows us to create a variety of algorithms, including SSS* and DUAL*. In effect, we formulate a best-first algorithm using depth-first search. Expressed in this framework SSS* is just a special case of Alpha-Beta, solving all of the perceived drawbacks of the algorithm. In practice, Alpha-Beta variants typically evaluate less nodes than SSS*. A new instance of this framework, MTD(f), out-performs SSS* and NegaScout, the Alpha-Beta variant of choice by practitioners.

Nearly Optimal Minimax Tree Search?

Knuth and Moore presented a theoretical lower bound on the number of leaves that any fixed-depth minimax tree-search algorithm traversing a uniform tree must explore, the so-called minimal tree. Since real-life minimax trees are not uniform, the exact size of this tree is not known for most applications. Further, most games have transpositions, implying that there exists a minimal graph which is smaller than the minimal tree. For three games (chess, Othello and checkers) we compute the size of the minimal tree and the minimal graph. Empirical evidence shows that in all three games, enhanced Alpha-Beta search is capable of building a tree that is close in size to that of the minimal graph. Hence, it appears game-playing programs build nearly optimal search trees. However, the conventional definition of the minimal graph is wrong. There are ways in which the size of the minimal graph can be reduced: by maximizing the number of transpositions in the search, and generating cutoffs using branches that lead to smaller search trees. The conventional definition of the minimal graph is just a left-most approximation. Calculating the size of the real minimal graph is too computationally intensive. However, upper bound approximations show it to be significantly smaller than the left-most minimal graph. Hence, it appears that game-playing programs are not searching as efficiently as is widely believed. Understanding the left-most and real minimal search graphs leads to some new ideas for enhancing Alpha-Beta search. One of them, enhanced transposition cutoffs, is shown to significantly reduce search tree size.

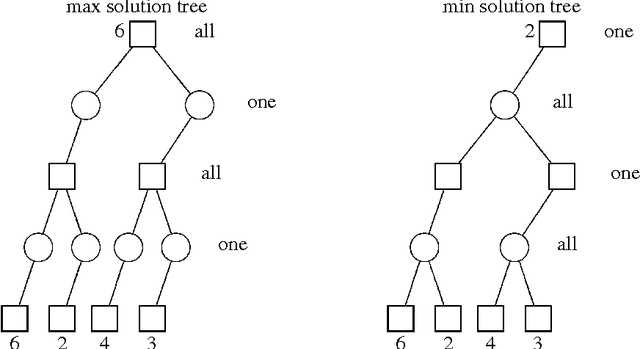
SSS* = Alpha-Beta + TT

In 1979 Stockman introduced the SSS* minimax search algorithm that domi- nates Alpha-Beta in the number of leaf nodes expanded. Further investigation of the algorithm showed that it had three serious drawbacks, which prevented its use by practitioners: it is difficult to understand, it has large memory requirements, and it is slow. This paper presents an alternate formulation of SSS*, in which it is implemented as a series of Alpha-Beta calls that use a transposition table (AB- SSS*). The reformulation solves all three perceived drawbacks of SSS*, making it a practical algorithm. Further, because the search is now based on Alpha-Beta, the extensive research on minimax search enhancements can be easily integrated into AB-SSS*. To test AB-SSS* in practise, it has been implemented in three state-of-the- art programs: for checkers, Othello and chess. AB-SSS* is comparable in performance to Alpha-Beta on leaf node count in all three games, making it a viable alternative to Alpha-Beta in practise. Whereas SSS* has usually been regarded as being entirely different from Alpha-Beta, it turns out to be just an Alpha-Beta enhancement, like null-window searching. This runs counter to published simulation results. Our research leads to the surprising result that iterative deepening versions of Alpha-Beta can expand fewer leaf nodes than iterative deepening versions of SSS* due to dynamic move re-ordering.

A New Paradigm for Minimax Search

This paper introduces a new paradigm for minimax game-tree search algo- rithms. MT is a memory-enhanced version of Pearls Test procedure. By changing the way MT is called, a number of best-first game-tree search algorithms can be simply and elegantly constructed (including SSS*). Most of the assessments of minimax search algorithms have been based on simulations. However, these simulations generally do not address two of the key ingredients of high performance game-playing programs: iterative deepening and memory usage. This paper presents experimental data from three game-playing programs (checkers, Othello and chess), covering the range from low to high branching factor. The improved move ordering due to iterative deepening and memory usage results in significantly different results from those portrayed in the literature. Whereas some simulations show Alpha-Beta expanding almost 100% more leaf nodes than other algorithms [12], our results showed variations of less than 20%. One new instance of our framework (MTD-f) out-performs our best alpha- beta searcher (aspiration NegaScout) on leaf nodes, total nodes and execution time. To our knowledge, these are the first reported results that compare both depth-first and best-first algorithms given the same amount of memory