Ariel Felner
Bidirectional Bounded-Suboptimal Heuristic Search with Consistent Heuristics
Nov 13, 2025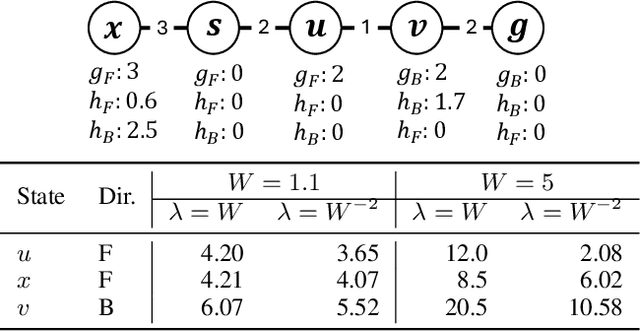
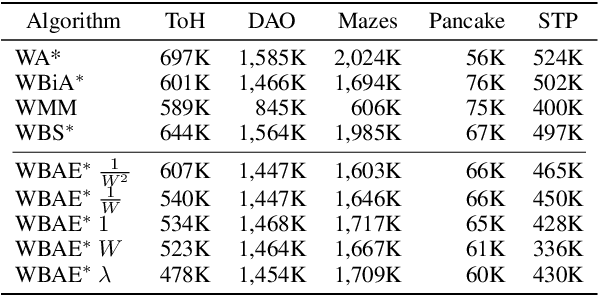

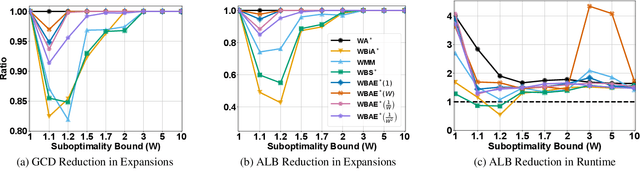
Abstract:Recent advancements in bidirectional heuristic search have yielded significant theoretical insights and novel algorithms. While most previous work has concentrated on optimal search methods, this paper focuses on bounded-suboptimal bidirectional search, where a bound on the suboptimality of the solution cost is specified. We build upon the state-of-the-art optimal bidirectional search algorithm, BAE*, designed for consistent heuristics, and introduce several variants of BAE* specifically tailored for the bounded-suboptimal context. Through experimental evaluation, we compare the performance of these new variants against other bounded-suboptimal bidirectional algorithms as well as the standard weighted A* algorithm. Our results demonstrate that each algorithm excels under distinct conditions, highlighting the strengths and weaknesses of each approach.
A Preprocessing Framework for Efficient Approximate Bi-Objective Shortest-Path Computation in the Presence of Correlated Objectives
May 28, 2025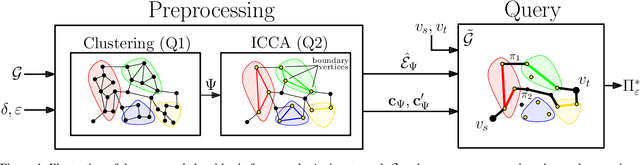



Abstract:The bi-objective shortest-path (BOSP) problem seeks to find paths between start and target vertices of a graph while optimizing two conflicting objective functions. We consider the BOSP problem in the presence of correlated objectives. Such correlations often occur in real-world settings such as road networks, where optimizing two positively correlated objectives, such as travel time and fuel consumption, is common. BOSP is generally computationally challenging as the size of the search space is exponential in the number of objective functions and the graph size. Bounded sub-optimal BOSP solvers such as A*pex alleviate this complexity by approximating the Pareto-optimal solution set rather than computing it exactly (given a user-provided approximation factor). As the correlation between objective functions increases, smaller approximation factors are sufficient for collapsing the entire Pareto-optimal set into a single solution. We leverage this insight to propose an efficient algorithm that reduces the search effort in the presence of correlated objectives. Our approach for computing approximations of the entire Pareto-optimal set is inspired by graph-clustering algorithms. It uses a preprocessing phase to identify correlated clusters within a graph and to generate a new graph representation. This allows a natural generalization of A*pex to run up to five times faster on DIMACS dataset instances, a standard benchmark in the field. To the best of our knowledge, this is the first algorithm proposed that efficiently and effectively exploits correlations in the context of bi-objective search while providing theoretical guarantees on solution quality.
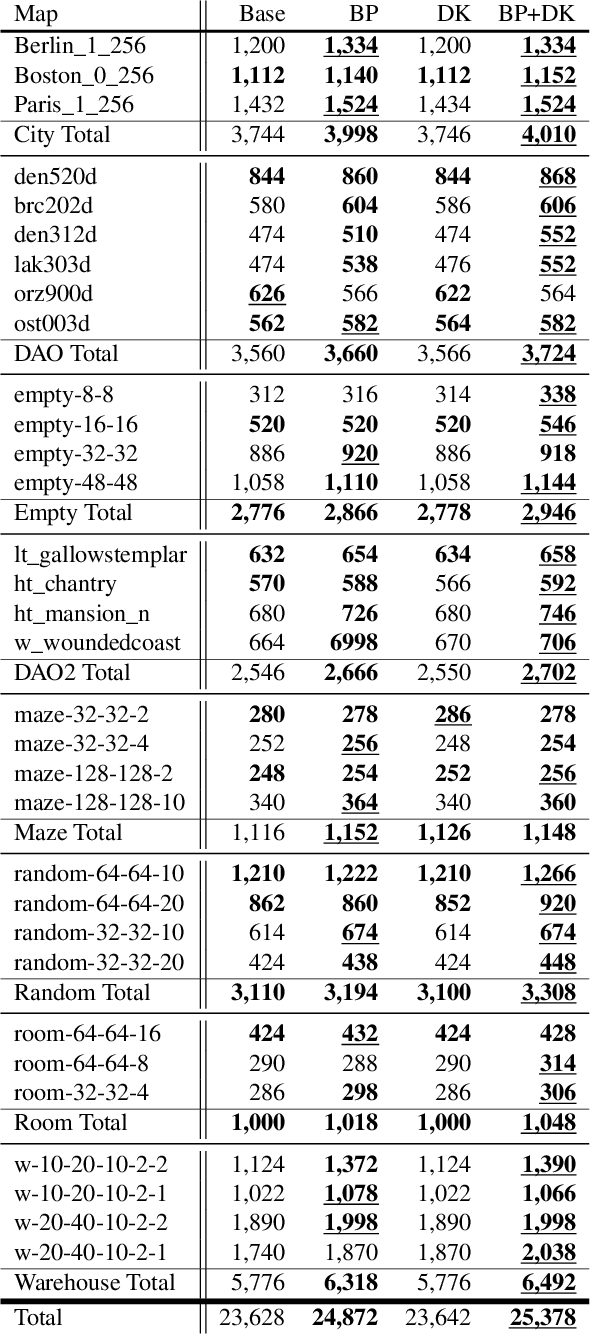
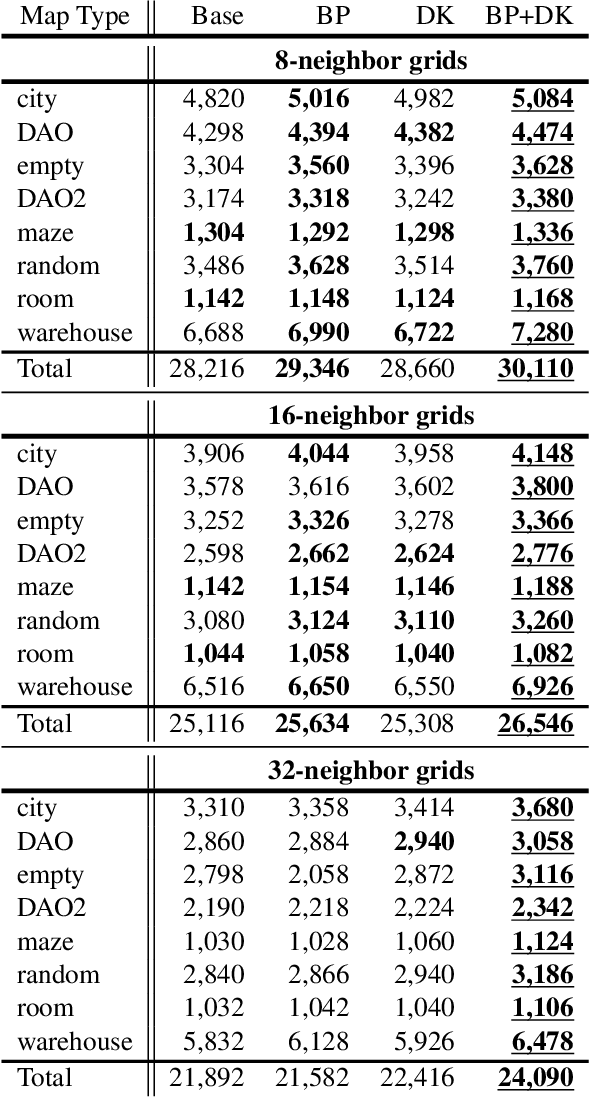
On Parallel External-Memory Bidirectional Search
Dec 30, 2024Abstract:Parallelization and External Memory (PEM) techniques have significantly enhanced the capabilities of search algorithms when solving large-scale problems. Previous research on PEM has primarily centered on unidirectional algorithms, with only one publication on bidirectional PEM that focuses on the meet-in-the-middle (MM) algorithm. Building upon this foundation, this paper presents a framework that integrates both uni- and bi-directional best-first search algorithms into this framework. We then develop a PEM variant of the state-of-the-art bidirectional heuristic search (\BiHS) algorithm BAE* (PEM-BAE*). As previous work on \BiHS did not focus on scaling problem sizes, this work enables us to evaluate bidirectional algorithms on hard problems. Empirical evaluation shows that PEM-BAE* outperforms the PEM variants of A* and the MM algorithm, as well as a parallel variant of IDA*. These findings mark a significant milestone, revealing that bidirectional search algorithms clearly outperform unidirectional search algorithms across several domains, even when equipped with state-of-the-art heuristics.
Clique Analysis and Bypassing in Continuous-Time Conflict-Based Search
Dec 26, 2023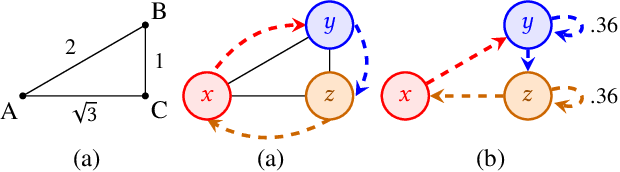
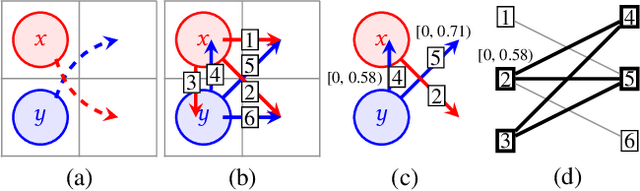
Abstract:While the study of unit-cost Multi-Agent Pathfinding (MAPF) problems has been popular, many real-world problems require continuous time and costs due to various movement models. In this context, this paper studies symmetry-breaking enhancements for Continuous-Time Conflict-Based Search (CCBS), a solver for continuous-time MAPF. Resolving conflict symmetries in MAPF can require an exponential amount of work. We adapt known enhancements from unit-cost domains for CCBS: bypassing, which resolves cost symmetries and biclique constraints which resolve spatial conflict symmetries. We formulate a novel combination of biclique constraints with disjoint splitting for spatial conflict symmetries. Finally, we show empirically that these enhancements yield a statistically significant performance improvement versus previous state of the art, solving problems for up to 10% or 20% more agents in the same amount of time on dense graphs.
Tightest Admissible Shortest Path
Aug 15, 2023

Abstract:The shortest path problem in graphs is fundamental to AI. Nearly all variants of the problem and relevant algorithms that solve them ignore edge-weight computation time and its common relation to weight uncertainty. This implies that taking these factors into consideration can potentially lead to a performance boost in relevant applications. Recently, a generalized framework for weighted directed graphs was suggested, where edge-weight can be computed (estimated) multiple times, at increasing accuracy and run-time expense. We build on this framework to introduce the problem of finding the tightest admissible shortest path (TASP); a path with the tightest suboptimality bound on the optimal cost. This is a generalization of the shortest path problem to bounded uncertainty, where edge-weight uncertainty can be traded for computational cost. We present a complete algorithm for solving TASP, with guarantees on solution quality. Empirical evaluation supports the effectiveness of this approach.
Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks
Jun 19, 2019
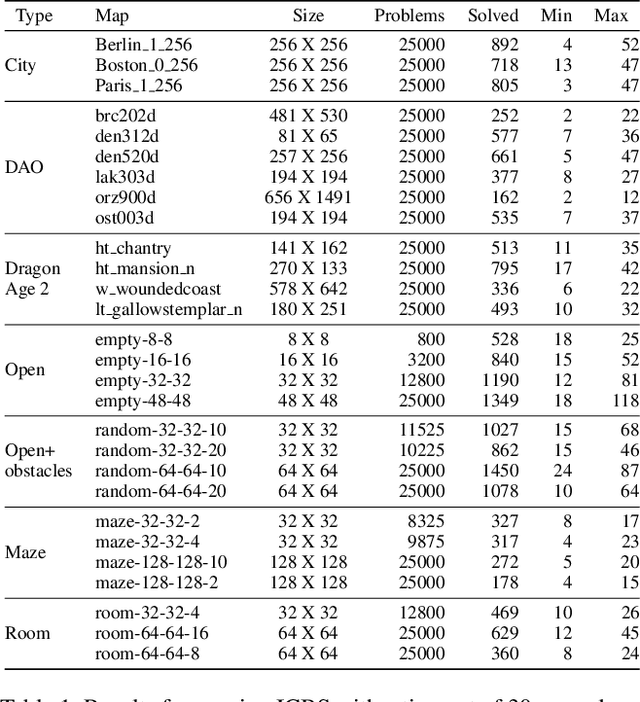
Abstract:The MAPF problem is the fundamental problem of planning paths for multiple agents, where the key constraint is that the agents will be able to follow these paths concurrently without colliding with each other. Applications of MAPF include automated warehouses and autonomous vehicles. Research on MAPF has been flourishing in the past couple of years. Different MAPF research papers make different assumptions, e.g., whether agents can traverse the same road at the same time, and have different objective functions, e.g., minimize makespan or sum of agents' actions costs. These assumptions and objectives are sometimes implicitly assumed or described informally. This makes it difficult to establish appropriate baselines for comparison in research papers, as well as making it difficult for practitioners to find the papers relevant to their concrete application. This paper aims to fill this gap and support researchers and practitioners by providing a unifying terminology for describing common MAPF assumptions and objectives. In addition, we also provide pointers to two MAPF benchmarks. In particular, we introduce a new grid-based benchmark for MAPF, and demonstrate experimentally that it poses a challenge to contemporary MAPF algorithms.
Multi-Agent Path Finding with Deadlines
Jun 11, 2018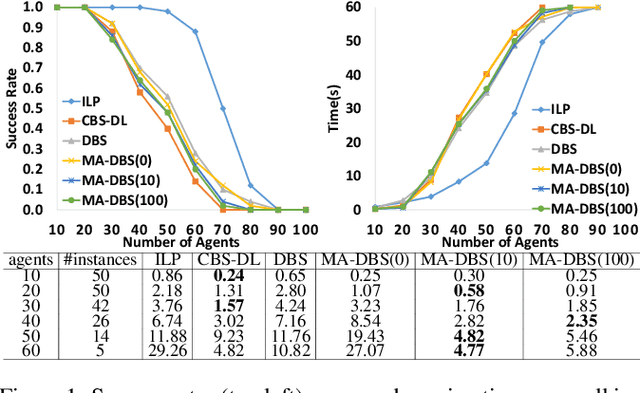
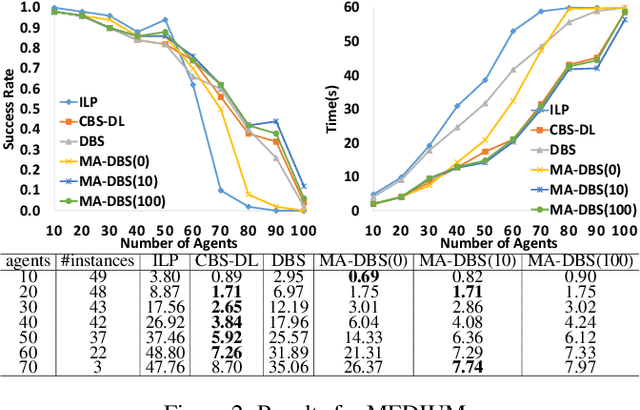
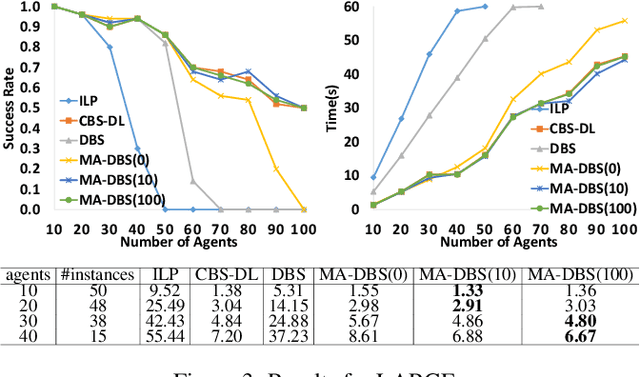
Abstract:We formalize Multi-Agent Path Finding with Deadlines (MAPF-DL). The objective is to maximize the number of agents that can reach their given goal vertices from their given start vertices within the deadline, without colliding with each other. We first show that MAPF-DL is NP-hard to solve optimally. We then present two classes of optimal algorithms, one based on a reduction of MAPF-DL to a flow problem and a subsequent compact integer linear programming formulation of the resulting reduced abstracted multi-commodity flow network and the other one based on novel combinatorial search algorithms. Our empirical results demonstrate that these MAPF-DL solvers scale well and each one dominates the other ones in different scenarios.
Multi-Agent Path Finding with Deadlines: Preliminary Results
May 13, 2018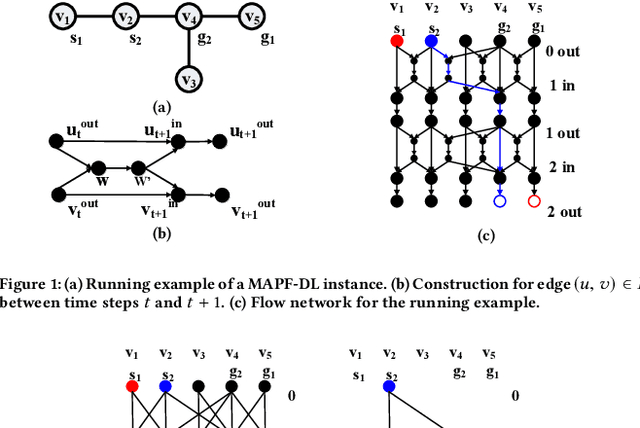
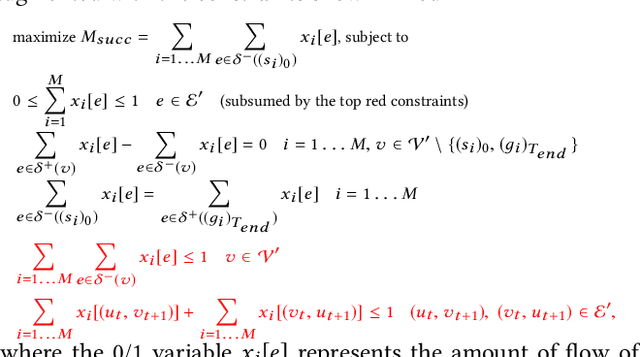
Abstract:We formalize the problem of multi-agent path finding with deadlines (MAPF-DL). The objective is to maximize the number of agents that can reach their given goal vertices from their given start vertices within a given deadline, without colliding with each other. We first show that the MAPF-DL problem is NP-hard to solve optimally. We then present an optimal MAPF-DL algorithm based on a reduction of the MAPF-DL problem to a flow problem and a subsequent compact integer linear programming formulation of the resulting reduced abstracted multi-commodity flow network.
Modifying Optimal SAT-based Approach to Multi-agent Path-finding Problem to Suboptimal Variants
Jul 02, 2017

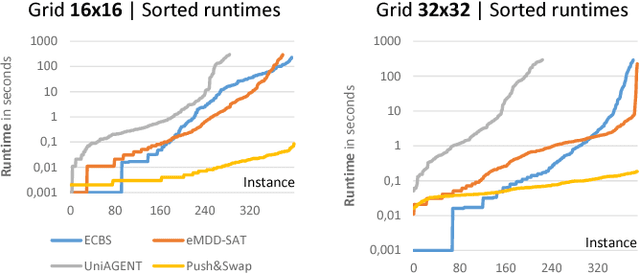

Abstract:In multi-agent path finding (MAPF) the task is to find non-conflicting paths for multiple agents. In this paper we focus on finding suboptimal solutions for MAPF for the sum-of-costs variant. Recently, a SAT-based approached was developed to solve this problem and proved beneficial in many cases when compared to other search-based solvers. In this paper, we present SAT-based unbounded- and bounded-suboptimal algorithms and compare them to relevant algorithms. Experimental results show that in many case the SAT-based solver significantly outperforms the search-based solvers.
Rational Deployment of Multiple Heuristics in IDA*
Nov 24, 2014



Abstract:Recent advances in metareasoning for search has shown its usefulness in improving numerous search algorithms. This paper applies rational metareasoning to IDA* when several admissible heuristics are available. The obvious basic approach of taking the maximum of the heuristics is improved upon by lazy evaluation of the heuristics, resulting in a variant known as Lazy IDA*. We introduce a rational version of lazy IDA* that decides whether to compute the more expensive heuristics or to bypass it, based on a myopic expected regret estimate. Empirical evaluation in several domains supports the theoretical results, and shows that rational lazy IDA* is a state-of-the-art heuristic combination method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge