Efficient Incremental Belief Updates Using Weighted Virtual Observations

We present an algorithmic solution to the problem of incremental belief updating in the context of Monte Carlo inference in Bayesian statistical models represented by probabilistic programs. Given a model and a sample-approximated posterior, our solution constructs a set of weighted observations to condition the model such that inference would result in the same posterior. This problem arises e.g. in multi-level modelling, incremental inference, inference in presence of privacy constraints. First, a set of virtual observations is selected, then, observation weights are found through a computationally efficient optimization procedure such that the reconstructed posterior coincides with or closely approximates the original posterior. We implement and apply the solution to a number of didactic examples and case studies, showing efficiency and robustness of our approach. The provided reference implementation is agnostic to the probabilistic programming language or the inference algorithm, and can be applied to most mainstream probabilistic programming environments.

Monitoring Time Series With Missing Values: a Deep Probabilistic Approach

Systems are commonly monitored for health and security through collection and streaming of multivariate time series. Advances in time series forecasting due to adoption of multilayer recurrent neural network architectures make it possible to forecast in high-dimensional time series, and identify and classify novelties early, based on subtle changes in the trends. However, mainstream approaches to multi-variate time series predictions do not handle well cases when the ongoing forecast must include uncertainty, nor they are robust to missing data. We introduce a new architecture for time series monitoring based on combination of state-of-the-art methods of forecasting in high-dimensional time series with full probabilistic handling of uncertainty. We demonstrate advantage of the architecture for time series forecasting and novelty detection, in particular with partially missing data, and empirically evaluate and compare the architecture to state-of-the-art approaches on a real-world data set.

Bob and Alice Go to a Bar: Reasoning About Future With Probabilistic Programs

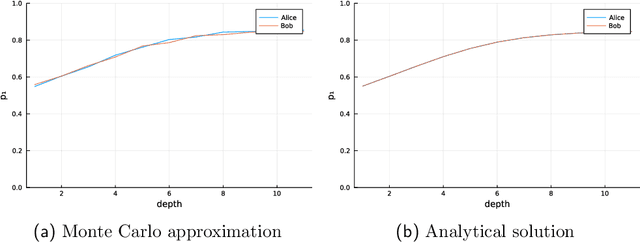
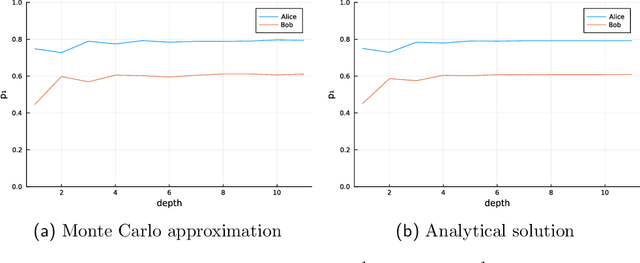
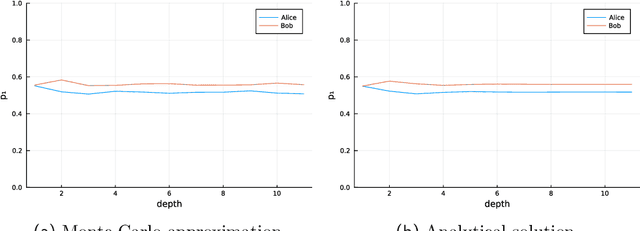
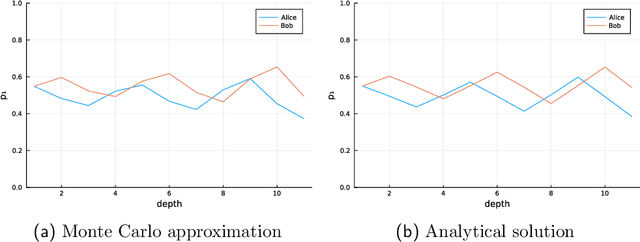
Agent preferences should be specified stochastically rather than deterministically. Planning as inference with stochastic preferences naturally describes agent behaviors, does not require introducing rewards and exponential weighing of behaviors, and allows to reason about agents using the solid foundation of Bayesian statistics. Stochastic conditioning is the formalism behind agents with stochastic preferences.

How To Train Your Program

We present a Bayesian approach to machine learning with probabilistic programs. In our approach, training on available data is implemented as inference on a hierarchical model. The posterior distribution of model parameters is then used to \textit{stochastically condition} a complementary model, such that inference on new data yields the same posterior distribution of latent parameters corresponding to the new data as inference on a hierachical model on the combination of both previously available and new data, at a lower computation cost. We frame the approach as a design pattern of probabilistic programming referred to herein as `stump and fungus', and illustrate realization of the pattern on a didactic case study.

Bayesian Policy Search for Stochastic Domains

AI planning can be cast as inference in probabilistic models, and probabilistic programming was shown to be capable of policy search in partially observable domains. Prior work introduces policy search through Markov chain Monte Carlo in deterministic domains, as well as adapts black-box variational inference to stochastic domains, however not in the strictly Bayesian sense. In this work, we cast policy search in stochastic domains as a Bayesian inference problem and provide a scheme for encoding such problems as nested probabilistic programs. We argue that probabilistic programs for policy search in stochastic domains should involve nested conditioning, and provide an adaption of Lightweight Metropolis-Hastings (LMH) for robust inference in such programs. We apply the proposed scheme to stochastic domains and show that policies of similar quality are learned, despite a simpler and more general inference algorithm. We believe that the proposed variant of LMH is novel and applicable to a wider class of probabilistic programs with nested conditioning.

Probabilistic Programs with Stochastic Conditioning

We propose to distinguish between deterministic conditioning, that is, conditioning on a sample from the joint data distribution, and stochastic conditioning, that is, conditioning on the distribution of the observable variable. Mostly, probabilistic programs follow the Bayesian approach by choosing a prior distribution of parameters and conditioning on observations. In a basic setting, individual observations are In a basic setting, individual observations are samples from the joint data distribution. However, observations may also be independent samples from marginal data distributions of each observable variable, summary statistics, or even data distributions themselves . These cases naturally appear in real life scenarios: samples from marginal distributions arise when different observations are collected by different parties, summary statistics (mean, variance, and quantiles) are often used to represent data collected over a large population, and data distributions may represent uncertainty during inference about future states of the world, that is, in planning. Probabilistic programming languages and frameworks which support conditioning on samples from the joint data distribution are not directly capable of expressing such models. We define the notion of stochastic conditioning and describe extensions of known general inference algorithms to probabilistic programs with stochastic conditioning. In case studies we provide probabilistic programs for several problems of statistical inference which are impossible or difficult to approach otherwise, perform inference on the programs, and analyse the results.

Stochastically Differentiable Probabilistic Programs

Probabilistic programs with mixed support (both continuous and discrete latent random variables) commonly appear in many probabilistic programming systems (PPSs). However, the existence of the discrete random variables prohibits many basic gradient-based inference engines, which makes the inference procedure on such models particularly challenging. Existing PPSs either require the user to manually marginalize out the discrete variables or to perform a composing inference by running inference separately on discrete and continuous variables. The former is infeasible in most cases whereas the latter has some fundamental shortcomings. We present a novel approach to run inference efficiently and robustly in such programs using stochastic gradient Markov Chain Monte Carlo family of algorithms. We compare our stochastic gradient-based inference algorithm against conventional baselines in several important cases of probabilistic programs with mixed support, and demonstrate that it outperforms existing composing inference baselines and works almost as well as inference in marginalized versions of the programs, but with less programming effort and at a lower computation cost.

Stochastic Probabilistic Programs

We introduce the notion of a stochastic probabilistic program and present a reference implementation of a probabilistic programming facility supporting specification of stochastic probabilistic programs and inference in them. Stochastic probabilistic programs allow straightforward specification and efficient inference in models with nuisance parameters, noise, and nondeterminism. We give several examples of stochastic probabilistic programs, and compare the programs with corresponding deterministic probabilistic programs in terms of model specification and inference. We conclude with discussion of open research topics and related work.

Warped Input Gaussian Processes for Time Series Forecasting

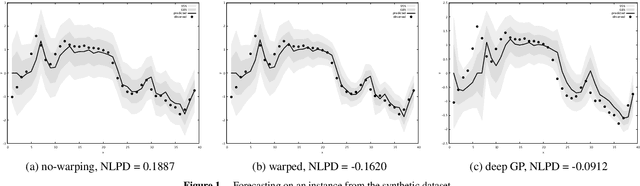
We introduce a Gaussian process-based model for handling of non-stationarity. The warping is achieved non-parametrically, through imposing a prior on the relative change of distance between subsequent observation inputs. The model allows the use of general gradient optimization algorithms for training and incurs only a small computational overhead on training and prediction. The model finds its applications in forecasting in non-stationary time series with either gradually varying volatility, presence of change points, or a combination thereof. We evaluate the model on synthetic and real-world time series data comparing against both baseline and known state-of-the-art approaches and show that the model exhibits state-of-the-art forecasting performance at a lower implementation and computation cost.

Deployable probabilistic programming

We propose design guidelines for a probabilistic programming facility suitable for deployment as a part of a production software system. As a reference implementation, we introduce Infergo, a probabilistic programming facility for Go, a modern programming language of choice for server-side software development. We argue that a similar probabilistic programming facility can be added to most modern general-purpose programming languages. Probabilistic programming enables automatic tuning of program parameters and algorithmic decision making through probabilistic inference based on the data. To facilitate addition of probabilistic programming capabilities to other programming languages, we share implementation choices and techniques employed in development of Infergo. We illustrate applicability of Infergo to various use cases on case studies, and evaluate Infergo's performance on several benchmarks, comparing Infergo to dedicated inference-centric probabilistic programming frameworks.