Uncertainty Estimation based on Geometric Separation

In machine learning, accurately predicting the probability that a specific input is correct is crucial for risk management. This process, known as uncertainty (or confidence) estimation, is particularly important in mission-critical applications such as autonomous driving. In this work, we put forward a novel geometric-based approach for improving uncertainty estimations in machine learning models. Our approach involves using the geometric distance of the current input from existing training inputs as a signal for estimating uncertainty, and then calibrating this signal using standard post-hoc techniques. We demonstrate that our method leads to more accurate uncertainty estimations than recently proposed approaches through extensive evaluation on a variety of datasets and models. Additionally, we optimize our approach so that it can be implemented on large datasets in near real-time applications, making it suitable for time-sensitive scenarios.

A Geometric Method for Improved Uncertainty Estimation in Real-time

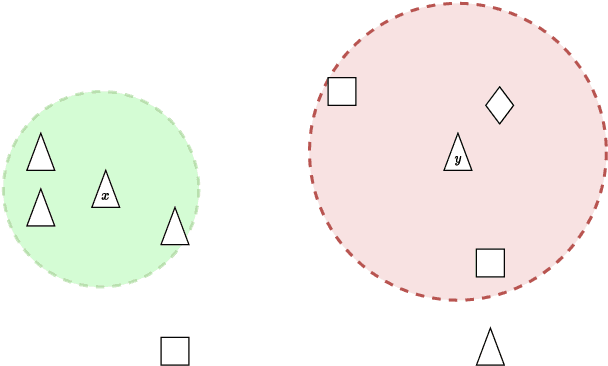
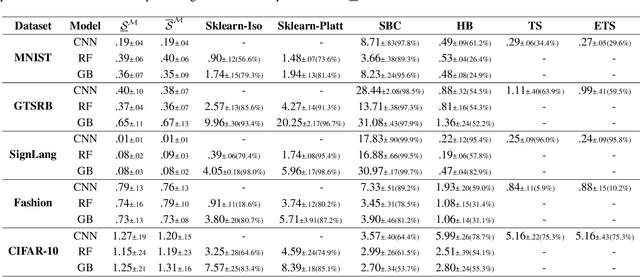
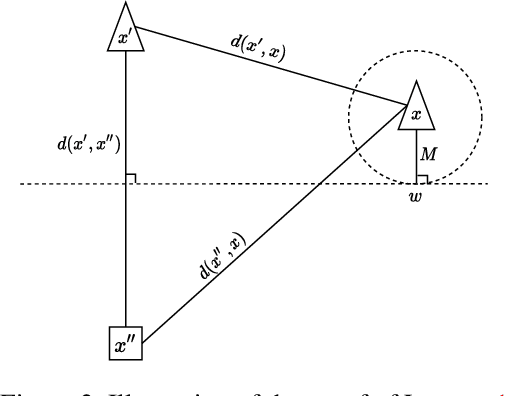
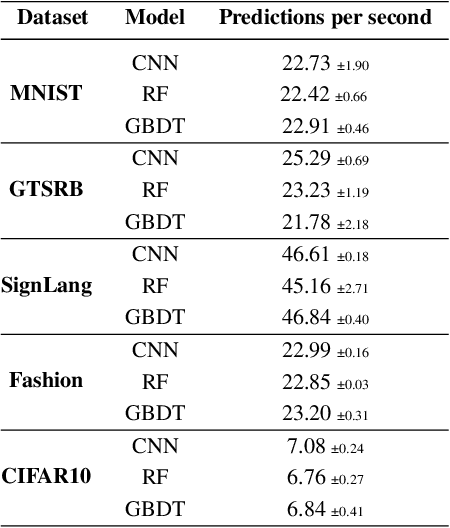
Machine learning classifiers are probabilistic in nature, and thus inevitably involve uncertainty. Predicting the probability of a specific input to be correct is called uncertainty (or confidence) estimation and is crucial for risk management. Post-hoc model calibrations can improve models' uncertainty estimations without the need for retraining, and without changing the model. Our work puts forward a geometric-based approach for uncertainty estimation. Roughly speaking, we use the geometric distance of the current input from the existing training inputs as a signal for estimating uncertainty and then calibrate that signal (instead of the model's estimation) using standard post-hoc calibration techniques. We show that our method yields better uncertainty estimations than recently proposed approaches by extensively evaluating multiple datasets and models. In addition, we also demonstrate the possibility of performing our approach in near real-time applications. Our code is available at our Github https://github.com/NoSleepDeveloper/Geometric-Calibrator.

Embedding Directed Graphs in Potential Fields Using FastMap-D

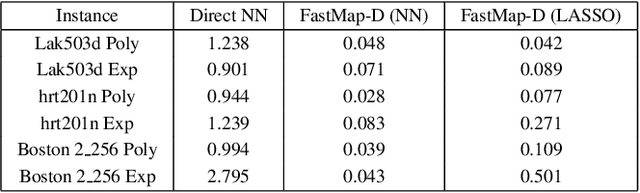
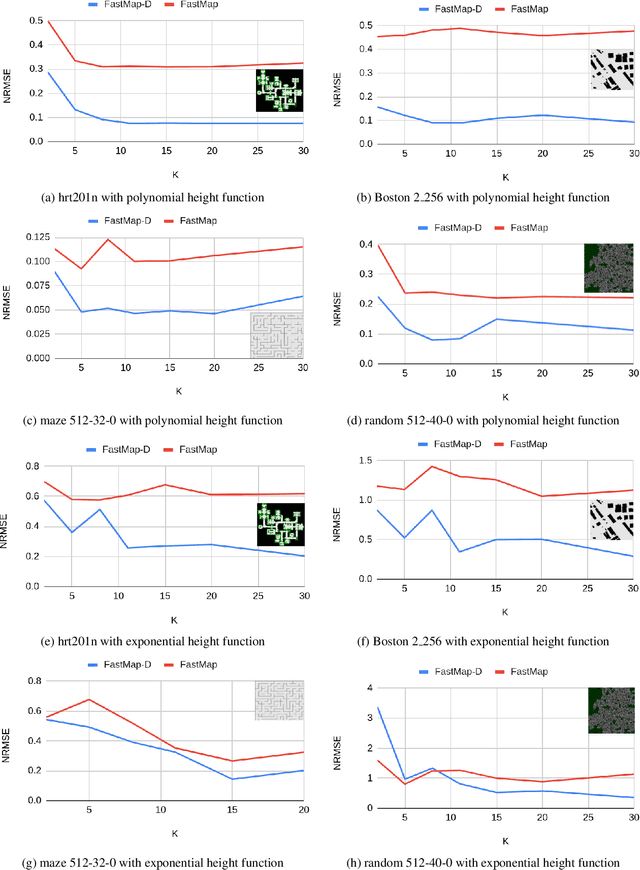
Embedding undirected graphs in a Euclidean space has many computational benefits. FastMap is an efficient embedding algorithm that facilitates a geometric interpretation of problems posed on undirected graphs. However, Euclidean distances are inherently symmetric and, thus, Euclidean embeddings cannot be used for directed graphs. In this paper, we present FastMap-D, an efficient generalization of FastMap to directed graphs. FastMap-D embeds vertices using a potential field to capture the asymmetry between the pairwise distances in directed graphs. FastMap-D learns a potential function to define the potential field using a machine learning module. In experiments on various kinds of directed graphs, we demonstrate the advantage of FastMap-D over other approaches.

Multi-Agent Pathfinding: Definitions, Variants, and Benchmarks

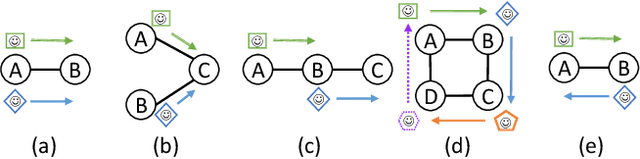
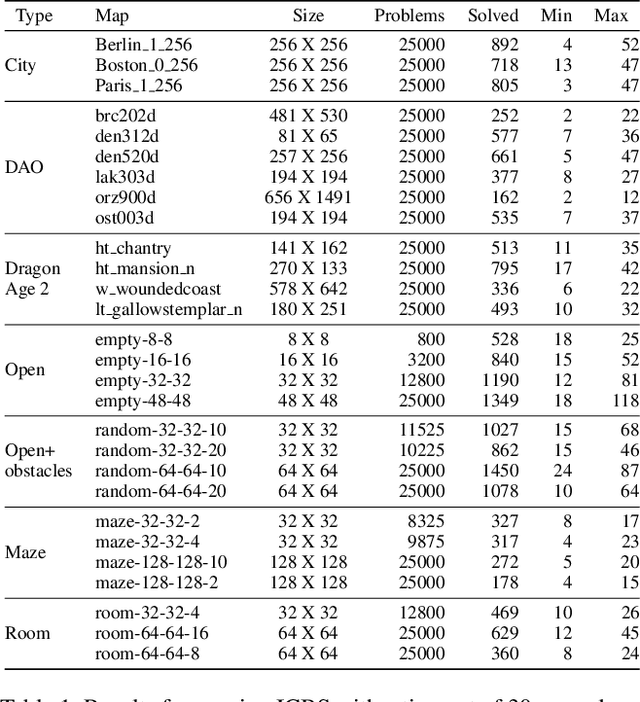
The MAPF problem is the fundamental problem of planning paths for multiple agents, where the key constraint is that the agents will be able to follow these paths concurrently without colliding with each other. Applications of MAPF include automated warehouses and autonomous vehicles. Research on MAPF has been flourishing in the past couple of years. Different MAPF research papers make different assumptions, e.g., whether agents can traverse the same road at the same time, and have different objective functions, e.g., minimize makespan or sum of agents' actions costs. These assumptions and objectives are sometimes implicitly assumed or described informally. This makes it difficult to establish appropriate baselines for comparison in research papers, as well as making it difficult for practitioners to find the papers relevant to their concrete application. This paper aims to fill this gap and support researchers and practitioners by providing a unifying terminology for describing common MAPF assumptions and objectives. In addition, we also provide pointers to two MAPF benchmarks. In particular, we introduce a new grid-based benchmark for MAPF, and demonstrate experimentally that it poses a challenge to contemporary MAPF algorithms.

Position Paper: From Multi-Agent Pathfinding to Pipe Routing

The 2D Multi-Agent Path Finding (MAPF) problem aims at finding collision-free paths for a number of agents, from a set of start locations to a set of goal positions in a known 2D environment. MAPF has been studied in theoretical computer science, robotics, and artificial intelligence over several decades, due to its importance for robot navigation. It is currently experiencing significant scientific progress due to its relevance in automated warehousing (such as those operated by Amazon) and in other contemporary application areas. In this paper, we demonstrate that many recently developed MAPF algorithms apply more broadly than currently believed in the MAPF research community. In particular, we describe the 3D Pipe Routing (PR) problem, which aims at placing collision-free pipes from given start locations to given goal locations in a known 3D environment. The MAPF and PR problems are similar: a solution to a MAPF instance is a set of blocked cells in x-y-t space, while a solution to the corresponding PR instance is a set of blocked cells in x-y-z space. We show how to use this similarity to apply several recently developed MAPF algorithms to the PR problem, and discuss their performance on abstract PR instances. We also discuss further research necessary to tackle real-world pipe-routing instances of interest to industry today. This opens up a new direction of industrial relevance for the MAPF research community.

Overview: A Hierarchical Framework for Plan Generation and Execution in Multi-Robot Systems

The authors present an overview of a hierarchical framework for coordinating task- and motion-level operations in multirobot systems. Their framework is based on the idea of using simple temporal networks to simultaneously reason about precedence/causal constraints required for task-level coordination and simple temporal constraints required to take some kinematic constraints of robots into account. In the plan-generation phase, the framework provides a computationally scalable method for generating plans that achieve high-level tasks for groups of robots and take some of their kinematic constraints into account. In the plan-execution phase, the framework provides a method for absorbing an imperfect plan execution to avoid time-consuming re-planning in many cases. The authors use the multirobot path-planning problem as a case study to present the key ideas behind their framework for the long-term autonomy of multirobot systems.

The FastMap Algorithm for Shortest Path Computations

We present a new preprocessing algorithm for embedding the nodes of a given edge-weighted undirected graph into a Euclidean space. The Euclidean distance between any two nodes in this space approximates the length of the shortest path between them in the given graph. Later, at runtime, a shortest path between any two nodes can be computed with A* search using the Euclidean distances as heuristic. Our preprocessing algorithm, called FastMap, is inspired by the data mining algorithm of the same name and runs in near-linear time. Hence, FastMap is orders of magnitude faster than competing approaches that produce a Euclidean embedding using Semidefinite Programming. FastMap also produces admissible and consistent heuristics and therefore guarantees the generation of shortest paths. Moreover, FastMap applies to general undirected graphs for which many traditional heuristics, such as the Manhattan Distance heuristic, are not well defined. Empirically, we demonstrate that A* search using the FastMap heuristic is competitive with A* search using other state-of-the-art heuristics, such as the Differential heuristic.

Feasibility Study: Moving Non-Homogeneous Teams in Congested Video Game Environments

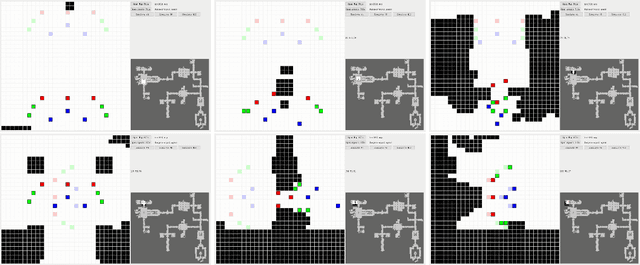
Multi-agent path finding (MAPF) is a well-studied problem in artificial intelligence, where one needs to find collision-free paths for agents with given start and goal locations. In video games, agents of different types often form teams. In this paper, we demonstrate the usefulness of MAPF algorithms from artificial intelligence for moving such non-homogeneous teams in congested video game environments.

Rapid Randomized Restarts for Multi-Agent Path Finding Solvers

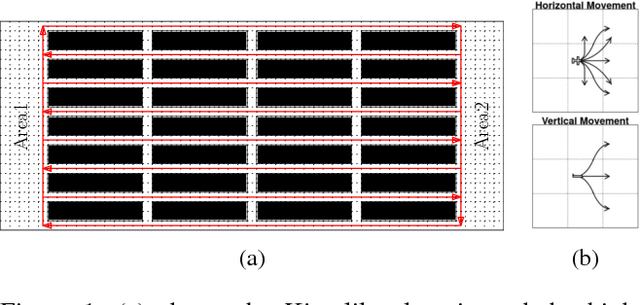
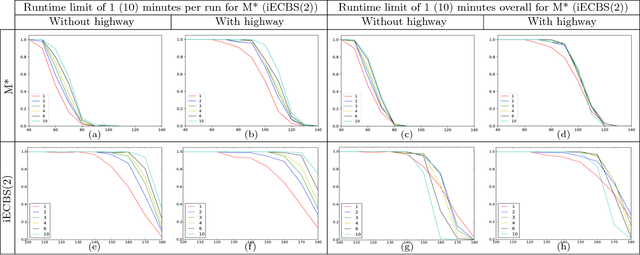
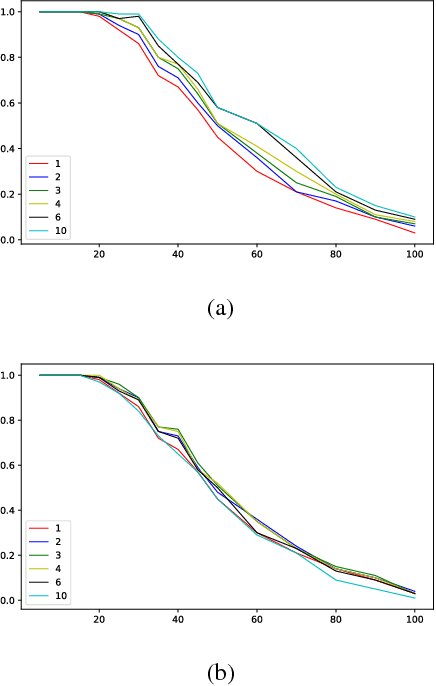
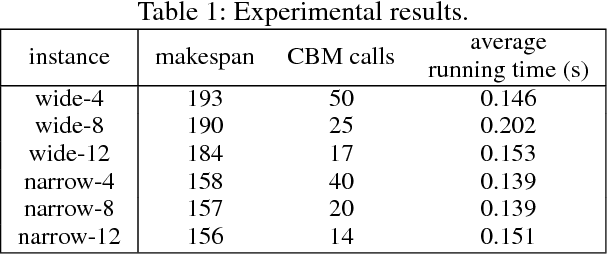
Multi-Agent Path Finding (MAPF) is an NP-hard problem well studied in artificial intelligence and robotics. It has many real-world applications for which existing MAPF solvers use various heuristics. However, these solvers are deterministic and perform poorly on "hard" instances typically characterized by many agents interfering with each other in a small region. In this paper, we enhance MAPF solvers with randomization and observe that they exhibit heavy-tailed distributions of runtimes on hard instances. This leads us to develop simple rapid randomized restart (RRR) strategies with the intuition that, given a hard instance, multiple short runs have a better chance of solving it compared to one long run. We validate this intuition through experiments and show that our RRR strategies indeed boost the performance of state-of-the-art MAPF solvers such as iECBS and M*.

Path Planning with Kinematic Constraints for Robot Groups

Path planning for multiple robots is well studied in the AI and robotics communities. For a given discretized environment, robots need to find collision-free paths to a set of specified goal locations. Robots can be fully anonymous, non-anonymous, or organized in groups. Although powerful solvers for this abstract problem exist, they make simplifying assumptions by ignoring kinematic constraints, making it difficult to use the resulting plans on actual robots. In this paper, we present a solution which takes kinematic constraints, such as maximum velocities, into account, while guaranteeing a user-specified minimum safety distance between robots. We demonstrate our approach in simulation and on real robots in 2D and 3D environments.