Uncertainty Estimation based on Geometric Separation

In machine learning, accurately predicting the probability that a specific input is correct is crucial for risk management. This process, known as uncertainty (or confidence) estimation, is particularly important in mission-critical applications such as autonomous driving. In this work, we put forward a novel geometric-based approach for improving uncertainty estimations in machine learning models. Our approach involves using the geometric distance of the current input from existing training inputs as a signal for estimating uncertainty, and then calibrating this signal using standard post-hoc techniques. We demonstrate that our method leads to more accurate uncertainty estimations than recently proposed approaches through extensive evaluation on a variety of datasets and models. Additionally, we optimize our approach so that it can be implemented on large datasets in near real-time applications, making it suitable for time-sensitive scenarios.

A Geometric Method for Improved Uncertainty Estimation in Real-time

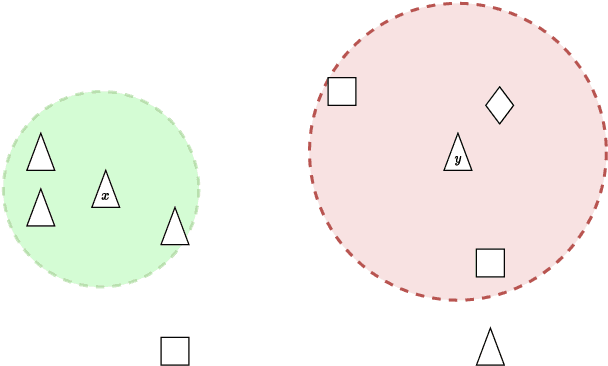
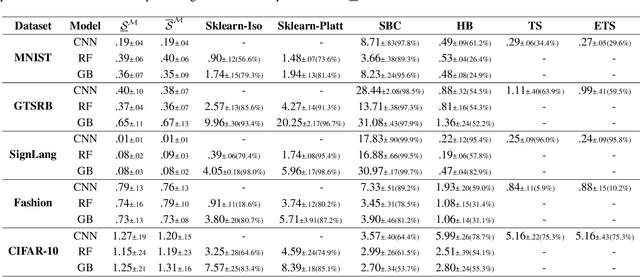
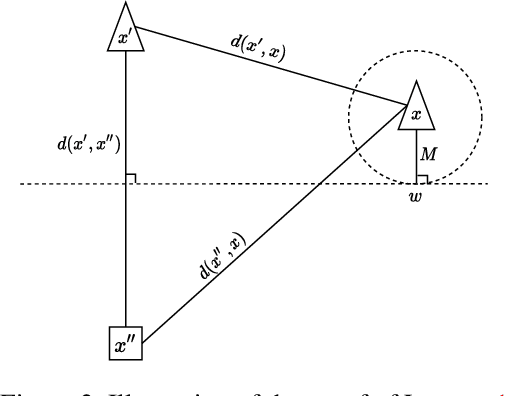
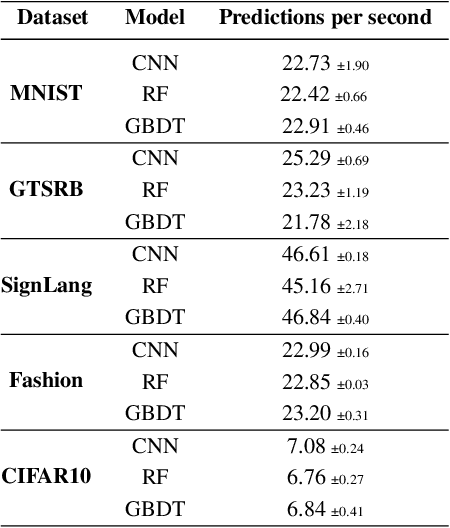
Machine learning classifiers are probabilistic in nature, and thus inevitably involve uncertainty. Predicting the probability of a specific input to be correct is called uncertainty (or confidence) estimation and is crucial for risk management. Post-hoc model calibrations can improve models' uncertainty estimations without the need for retraining, and without changing the model. Our work puts forward a geometric-based approach for uncertainty estimation. Roughly speaking, we use the geometric distance of the current input from the existing training inputs as a signal for estimating uncertainty and then calibrate that signal (instead of the model's estimation) using standard post-hoc calibration techniques. We show that our method yields better uncertainty estimations than recently proposed approaches by extensively evaluating multiple datasets and models. In addition, we also demonstrate the possibility of performing our approach in near real-time applications. Our code is available at our Github https://github.com/NoSleepDeveloper/Geometric-Calibrator.

QUIC-FL: Quick Unbiased Compression for Federated Learning

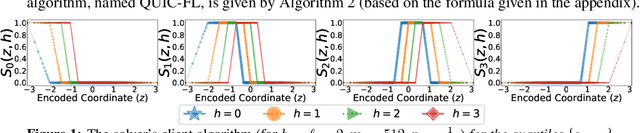
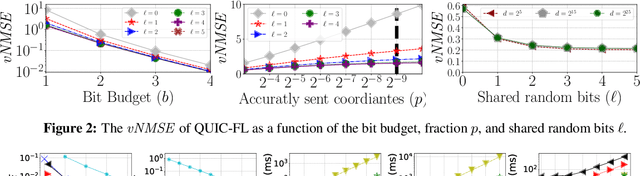
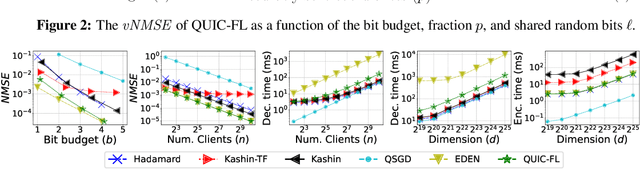
Distributed Mean Estimation (DME) is a fundamental building block in communication efficient federated learning. In DME, clients communicate their lossily compressed gradients to the parameter server, which estimates the average and updates the model. State of the art DME techniques apply either unbiased quantization methods, resulting in large estimation errors, or biased quantization methods, where unbiasing the result requires that the server decodes each gradient individually, which markedly slows the aggregation time. In this paper, we propose QUIC-FL, a DME algorithm that achieves the best of all worlds. QUIC-FL is unbiased, offers fast aggregation time, and is competitive with the most accurate (slow aggregation) DME techniques. To achieve this, we formalize the problem in a novel way that allows us to use standard solvers to design near-optimal unbiased quantization schemes.

Verifying Robustness of Gradient Boosted Models

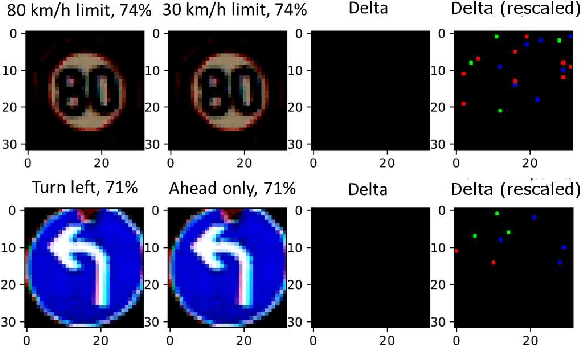
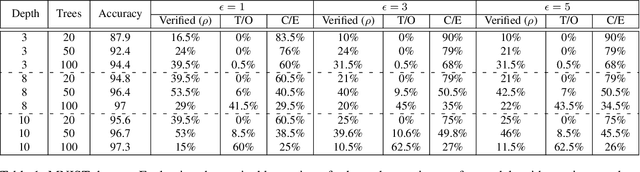
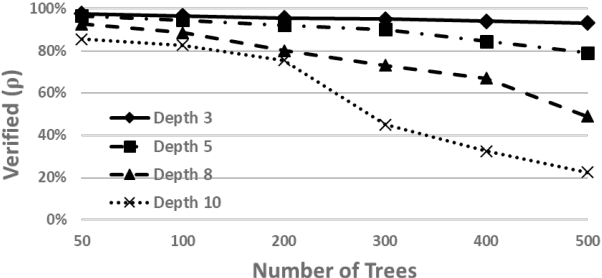
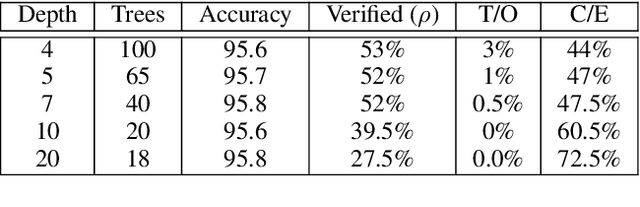
Gradient boosted models are a fundamental machine learning technique. Robustness to small perturbations of the input is an important quality measure for machine learning models, but the literature lacks a method to prove the robustness of gradient boosted models. This work introduces VeriGB, a tool for quantifying the robustness of gradient boosted models. VeriGB encodes the model and the robustness property as an SMT formula, which enables state of the art verification tools to prove the model's robustness. We extensively evaluate VeriGB on publicly available datasets and demonstrate a capability for verifying large models. Finally, we show that some model configurations tend to be inherently more robust than others.