Ran Ben Basat
University College London
HACK: Homomorphic Acceleration via Compression of the Key-Value Cache for Disaggregated LLM Inference
Feb 05, 2025

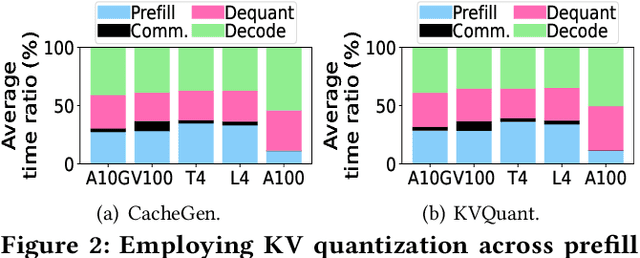

Abstract:Disaggregated Large Language Model (LLM) inference has gained popularity as it separates the computation-intensive prefill stage from the memory-intensive decode stage, avoiding the prefill-decode interference and improving resource utilization. However, transmitting Key-Value (KV) data between the two stages can be a bottleneck, especially for long prompts. Additionally, the computation time overhead for prefill and decode is key for optimizing Job Completion Time (JCT), and KV data size can become prohibitive for long prompts and sequences. Existing KV quantization methods can alleviate the transmission bottleneck and reduce memory requirements, but they introduce significant dequantization overhead, exacerbating the computation time. We propose Homomorphic Acceleration via Compression of the KV cache (HACK) for disaggregated LLM inference. HACK eliminates the heavy KV dequantization step, and directly performs computations on quantized KV data to approximate and reduce the cost of the expensive matrix-multiplication step. Extensive trace-driven experiments show that HACK reduces JCT by up to 70.9% compared to disaggregated LLM inference baseline and by up to 52.3% compared to state-of-the-art KV quantization methods.
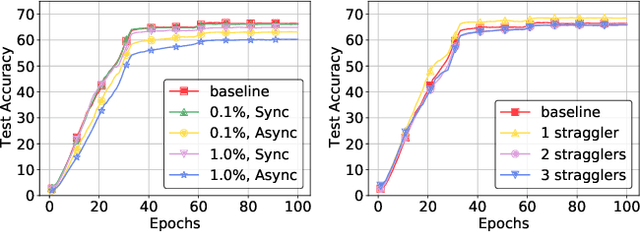
Beyond Throughput and Compression Ratios: Towards High End-to-end Utility of Gradient Compression
Jul 01, 2024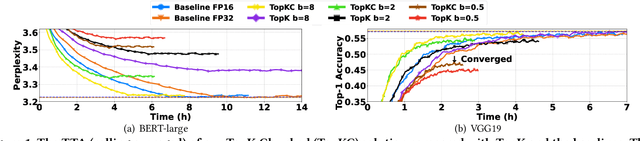

Abstract:Gradient aggregation has long been identified as a major bottleneck in today's large-scale distributed machine learning training systems. One promising solution to mitigate such bottlenecks is gradient compression, directly reducing communicated gradient data volume. However, in practice, many gradient compression schemes do not achieve acceleration of the training process while also preserving accuracy. In this work, we identify several common issues in previous gradient compression systems and evaluation methods. These issues include excessive computational overheads; incompatibility with all-reduce; and inappropriate evaluation metrics, such as not using an end-to-end metric or using a 32-bit baseline instead of a 16-bit baseline. We propose several general design and evaluation techniques to address these issues and provide guidelines for future work. Our preliminary evaluation shows that our techniques enhance the system's performance and provide a clearer understanding of the end-to-end utility of gradient compression methods.
THC: Accelerating Distributed Deep Learning Using Tensor Homomorphic Compression
Feb 16, 2023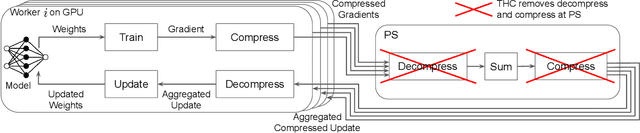

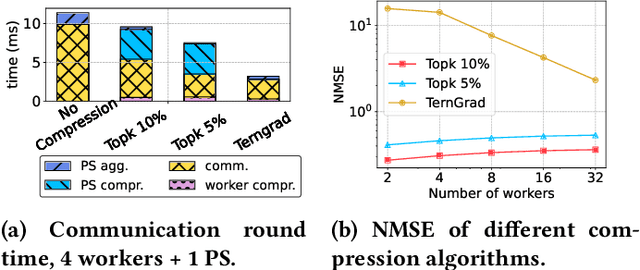
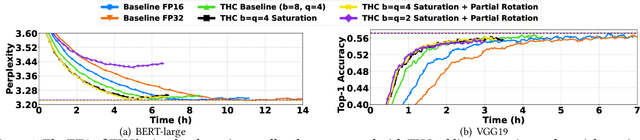
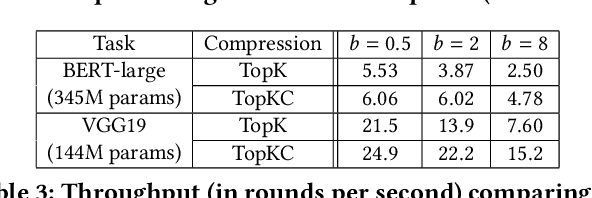
Abstract:Deep neural networks (DNNs) are the de-facto standard for essential use cases, such as image classification, computer vision, and natural language processing. As DNNs and datasets get larger, they require distributed training on increasingly larger clusters. A main bottleneck is then the resulting communication overhead where workers exchange model updates (i.e., gradients) on a per-round basis. To address this bottleneck and accelerate training, a widely-deployed approach is compression. However, previous deployments often apply bi-directional compression schemes by simply using a uni-directional gradient compression scheme in each direction. This results in significant computational overheads at the parameter server and increased compression error, leading to longer training and lower accuracy. We introduce Tensor Homomorphic Compression (THC), a novel bi-directional compression framework that enables the direct aggregation of compressed values while optimizing the bandwidth to accuracy tradeoff, thus eliminating the aforementioned overheads. Moreover, THC is compatible with in-network aggregation (INA), which allows for further acceleration. Evaluation over a testbed shows that THC improves time-to-accuracy in comparison to alternatives by up to 1.32x with a software PS and up to 1.51x using INA. Finally, we demonstrate that THC is scalable and tolerant for acceptable packet-loss rates.
QUIC-FL: Quick Unbiased Compression for Federated Learning
May 28, 2022
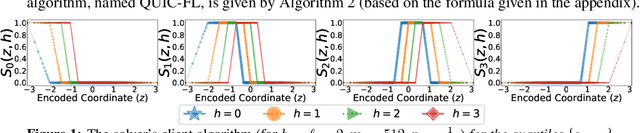
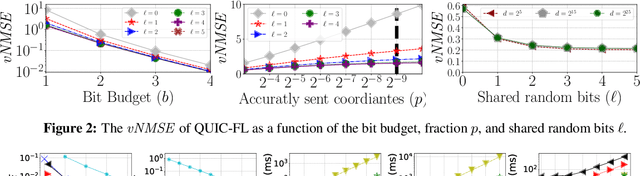
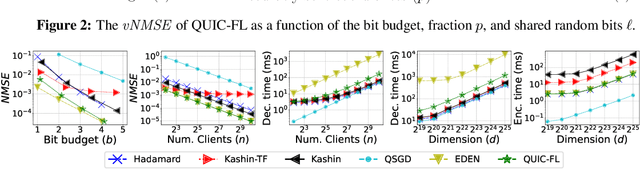
Abstract:Distributed Mean Estimation (DME) is a fundamental building block in communication efficient federated learning. In DME, clients communicate their lossily compressed gradients to the parameter server, which estimates the average and updates the model. State of the art DME techniques apply either unbiased quantization methods, resulting in large estimation errors, or biased quantization methods, where unbiasing the result requires that the server decodes each gradient individually, which markedly slows the aggregation time. In this paper, we propose QUIC-FL, a DME algorithm that achieves the best of all worlds. QUIC-FL is unbiased, offers fast aggregation time, and is competitive with the most accurate (slow aggregation) DME techniques. To achieve this, we formalize the problem in a novel way that allows us to use standard solvers to design near-optimal unbiased quantization schemes.
Communication-Efficient Federated Learning via Robust Distributed Mean Estimation
Aug 19, 2021
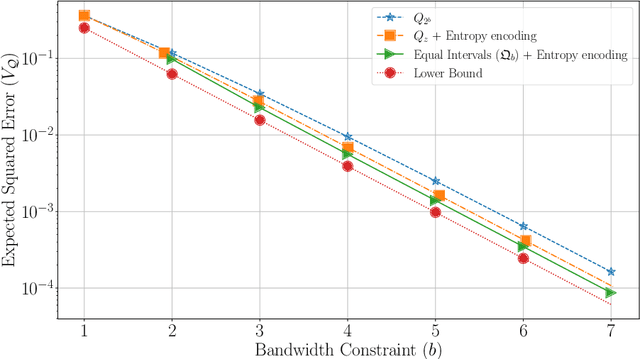
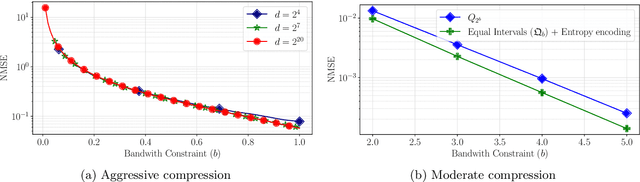
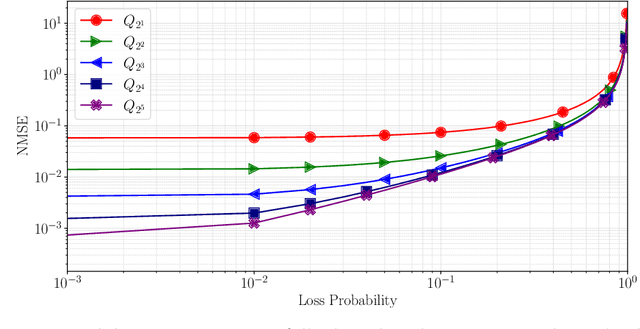
Abstract:Federated learning commonly relies on algorithms such as distributed (mini-batch) SGD, where multiple clients compute their gradients and send them to a central coordinator for averaging and updating the model. To optimize the transmission time and the scalability of the training process, clients often use lossy compression to reduce the message sizes. DRIVE is a recent state of the art algorithm that compresses gradients using one bit per coordinate (with some lower-order overhead). In this technical report, we generalize DRIVE to support any bandwidth constraint as well as extend it to support heterogeneous client resources and make it robust to packet loss.
DRIVE: One-bit Distributed Mean Estimation
Jun 02, 2021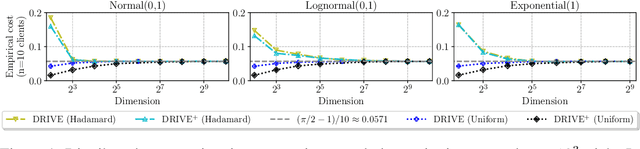
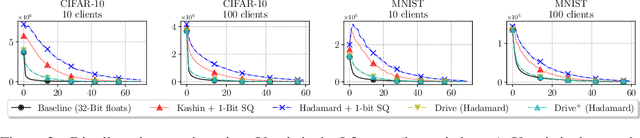
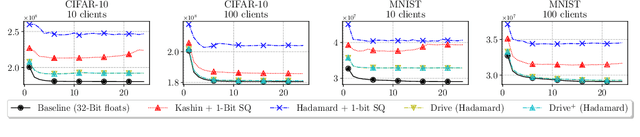
Abstract:We consider the problem where $n$ clients transmit $d$-dimensional real-valued vectors using $d(1+o(1))$ bits each, in a manner that allows the receiver to approximately reconstruct their mean. Such compression problems naturally arise in distributed and federated learning. We provide novel mathematical results and derive computationally efficient algorithms that are more accurate than previous compression techniques. We evaluate our methods on a collection of distributed and federated learning tasks, using a variety of datasets, and show a consistent improvement over the state of the art.
Learning Software Constraints via Installation Attempts
Apr 24, 2018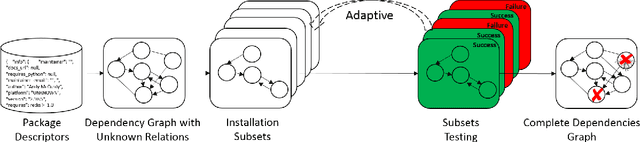

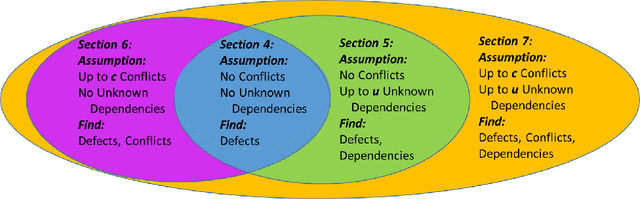
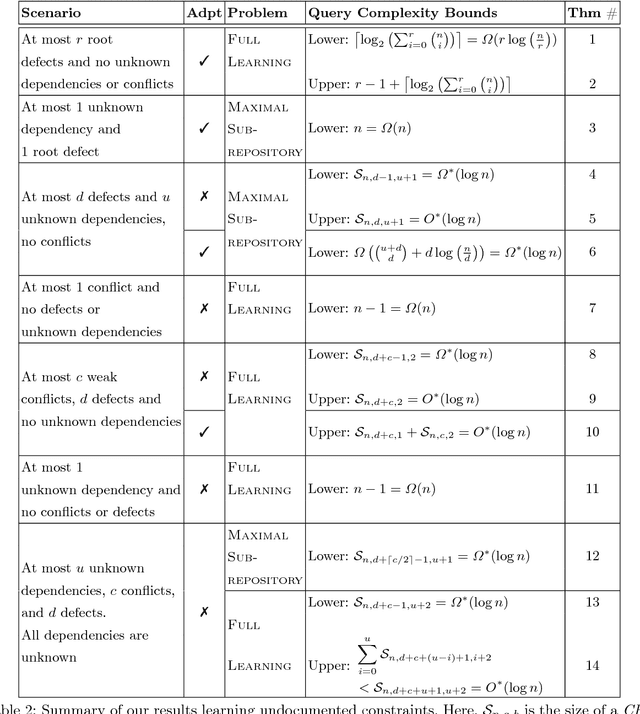
Abstract:Modern software systems are expected to be secure and contain all the latest features, even when new versions of software are released multiple times an hour. Each system may include many interacting packages. The problem of installing multiple dependent packages has been extensively studied in the past, yielding some promising solutions that work well in practice. However, these assume that the developers declare all the dependencies and conflicts between the packages. Oftentimes, the entire repository structure may not be known upfront, for example when packages are developed by different vendors. In this paper we present algorithms for learning dependencies, conflicts and defective packages from installation attempts. Our algorithms use combinatorial data structures to generate queries that test installations and discover the entire dependency structure. A query that the algorithms make corresponds to trying to install a subset of packages and getting a Boolean feedback on whether all constraints were satisfied in this subset. Our goal is to minimize the query complexity of the algorithms. We prove lower and upper bounds on the number of queries that these algorithms require to make for different settings of the problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge