NEUSIS: A Compositional Neuro-Symbolic Framework for Autonomous Perception, Reasoning, and Planning in Complex UAV Search Missions

This paper addresses the problem of autonomous UAV search missions, where a UAV must locate specific Entities of Interest (EOIs) within a time limit, based on brief descriptions in large, hazard-prone environments with keep-out zones. The UAV must perceive, reason, and make decisions with limited and uncertain information. We propose NEUSIS, a compositional neuro-symbolic system designed for interpretable UAV search and navigation in realistic scenarios. NEUSIS integrates neuro-symbolic visual perception, reasoning, and grounding (GRiD) to process raw sensory inputs, maintains a probabilistic world model for environment representation, and uses a hierarchical planning component (SNaC) for efficient path planning. Experimental results from simulated urban search missions using AirSim and Unreal Engine show that NEUSIS outperforms a state-of-the-art (SOTA) vision-language model and a SOTA search planning model in success rate, search efficiency, and 3D localization. These results demonstrate the effectiveness of our compositional neuro-symbolic approach in handling complex, real-world scenarios, making it a promising solution for autonomous UAV systems in search missions.

The divergence time of protein structures modelled by Markov matrices and its relation to the divergence of sequences

A complete time-parameterized statistical model quantifying the divergent evolution of protein structures in terms of the patterns of conservation of their secondary structures is inferred from a large collection of protein 3D structure alignments. This provides a better alternative to time-parameterized sequence-based models of protein relatedness, that have clear limitations dealing with twilight and midnight zones of sequence relationships. Since protein structures are far more conserved due to the selection pressure directly placed on their function, divergence time estimates can be more accurate when inferred from structures. We use the Bayesian and information-theoretic framework of Minimum Message Length to infer a time-parameterized stochastic matrix (accounting for perturbed structural states of related residues) and associated Dirichlet models (accounting for insertions and deletions during the evolution of protein domains). These are used in concert to estimate the Markov time of divergence of tertiary structures, a task previously only possible using proxies (like RMSD). By analyzing one million pairs of homologous structures, we yield a relationship between the Markov divergence time of structures and of sequences. Using these inferred models and the relationship between the divergence of sequences and structures, we demonstrate a competitive performance in secondary structure prediction against neural network architectures commonly employed for this task. The source code and supplementary information are downloadable from \url{http://lcb.infotech.monash.edu.au/sstsum}.

Position Paper: From Multi-Agent Pathfinding to Pipe Routing

The 2D Multi-Agent Path Finding (MAPF) problem aims at finding collision-free paths for a number of agents, from a set of start locations to a set of goal positions in a known 2D environment. MAPF has been studied in theoretical computer science, robotics, and artificial intelligence over several decades, due to its importance for robot navigation. It is currently experiencing significant scientific progress due to its relevance in automated warehousing (such as those operated by Amazon) and in other contemporary application areas. In this paper, we demonstrate that many recently developed MAPF algorithms apply more broadly than currently believed in the MAPF research community. In particular, we describe the 3D Pipe Routing (PR) problem, which aims at placing collision-free pipes from given start locations to given goal locations in a known 3D environment. The MAPF and PR problems are similar: a solution to a MAPF instance is a set of blocked cells in x-y-t space, while a solution to the corresponding PR instance is a set of blocked cells in x-y-z space. We show how to use this similarity to apply several recently developed MAPF algorithms to the PR problem, and discuss their performance on abstract PR instances. We also discuss further research necessary to tackle real-world pipe-routing instances of interest to industry today. This opens up a new direction of industrial relevance for the MAPF research community.

Redundant Sudoku Rules

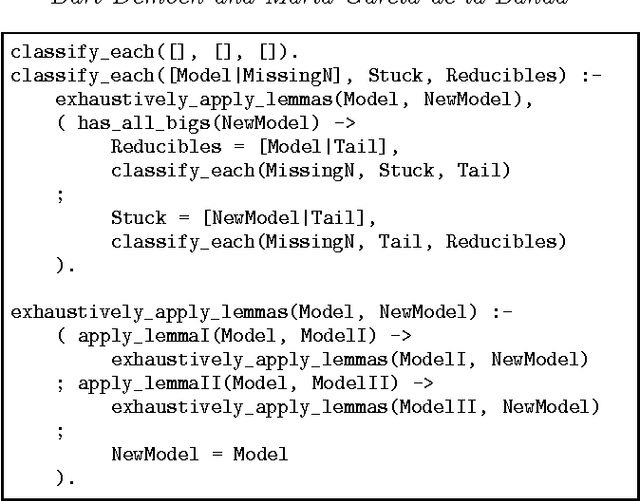
The rules of Sudoku are often specified using twenty seven \texttt{all\_different} constraints, referred to as the {\em big} \mrules. Using graphical proofs and exploratory logic programming, the following main and new result is obtained: many subsets of six of these big \mrules are redundant (i.e., they are entailed by the remaining twenty one \mrules), and six is maximal (i.e., removing more than six \mrules is not possible while maintaining equivalence). The corresponding result for binary inequality constraints, referred to as the {\em small} \mrules, is stated as a conjecture.