The divergence time of protein structures modelled by Markov matrices and its relation to the divergence of sequences

A complete time-parameterized statistical model quantifying the divergent evolution of protein structures in terms of the patterns of conservation of their secondary structures is inferred from a large collection of protein 3D structure alignments. This provides a better alternative to time-parameterized sequence-based models of protein relatedness, that have clear limitations dealing with twilight and midnight zones of sequence relationships. Since protein structures are far more conserved due to the selection pressure directly placed on their function, divergence time estimates can be more accurate when inferred from structures. We use the Bayesian and information-theoretic framework of Minimum Message Length to infer a time-parameterized stochastic matrix (accounting for perturbed structural states of related residues) and associated Dirichlet models (accounting for insertions and deletions during the evolution of protein domains). These are used in concert to estimate the Markov time of divergence of tertiary structures, a task previously only possible using proxies (like RMSD). By analyzing one million pairs of homologous structures, we yield a relationship between the Markov divergence time of structures and of sequences. Using these inferred models and the relationship between the divergence of sequences and structures, we demonstrate a competitive performance in secondary structure prediction against neural network architectures commonly employed for this task. The source code and supplementary information are downloadable from \url{http://lcb.infotech.monash.edu.au/sstsum}.

Subclasses of Class Function used to Implement Transformations of Statistical Models

A library of software for inductive inference guided by the Minimum Message Length (MML) principle was created previously. It contains various (object-oriented-) classes and subclasses of statistical Model and can be used to infer Models from given data sets in machine learning problems. Here transformations of statistical Models are considered and implemented within the library so as to have desirable properties from the object-oriented programming and mathematical points of view. The subclasses of class Function needed to do such transformations are defined.

Causal KL: Evaluating Causal Discovery

The two most commonly used criteria for assessing causal model discovery with artificial data are edit-distance and Kullback-Leibler divergence, measured from the true model to the learned model. Both of these metrics maximally reward the true model. However, we argue that they are both insufficiently discriminating in judging the relative merits of false models. Edit distance, for example, fails to distinguish between strong and weak probabilistic dependencies. KL divergence, on the other hand, rewards equally all statistically equivalent models, regardless of their different causal claims. We propose an augmented KL divergence, which we call Causal KL (CKL), which takes into account causal relationships which distinguish between observationally equivalent models. Results are presented for three variants of CKL, showing that Causal KL works well in practice.

Markov Blanket Discovery using Minimum Message Length

Causal discovery automates the learning of causal Bayesian networks from data and has been of active interest from their beginning. With the sourcing of large data sets off the internet, interest in scaling up to very large data sets has grown. One approach to this is to parallelize search using Markov Blanket (MB) discovery as a first step, followed by a process of combining MBs in a global causal model. We develop and explore three new methods of MB discovery using Minimum Message Length (MML) and compare them empirically to the best existing methods, whether developed specifically as MB discovery or as feature selection. Our best MML method is consistently competitive and has some advantageous features.

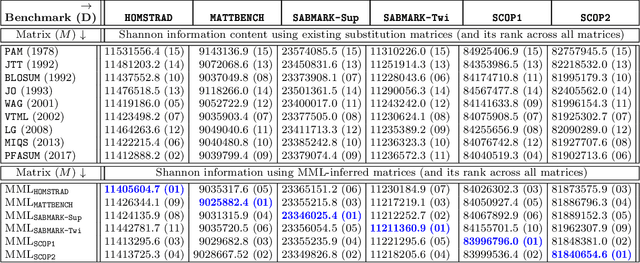
Bridging the Gaps in Statistical Models of Protein Alignment

This work demonstrates how a complete statistical model quantifying the evolution of pairs of aligned proteins can be constructed from a time-parameterised substitution matrix and a time-parameterised 3-state alignment machine. All parameters of such a model can be inferred from any benchmark data-set of aligned protein sequences. This allows us to examine nine well-known substitution matrices on six benchmarks curated using various structural alignment methods; any matrix that does not explicitly model a "time"-dependent Markov process is converted to a corresponding base-matrix that does. In addition, a new optimal matrix is inferred for each of the six benchmarks. Using Minimum Message Length (MML) inference, all 15 matrices are compared in terms of measuring the Shannon information content of each benchmark. This has resulted in a new and clear overall best performed time-dependent Markov matrix, MMLSUM, and its associated 3-state machine, whose properties we have analysed in this work. For standard use, the MMLSUM series of (log-odds) \textit{scoring} matrices derived from the above Markov matrix, are available at https://lcb.infotech.monash.edu.au/mmlsum.

Proving the NP-completeness of optimal moral graph triangulation

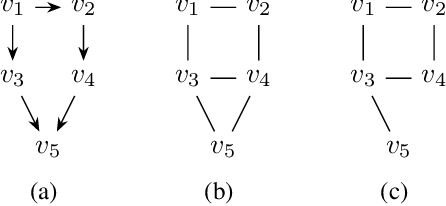
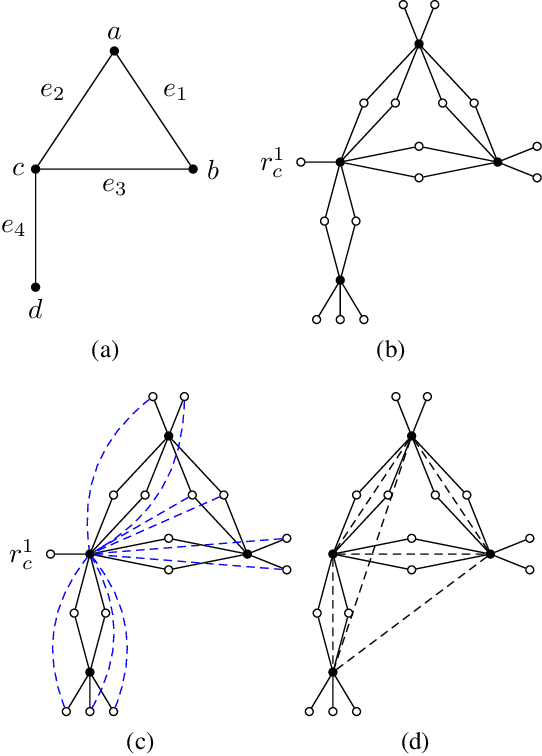
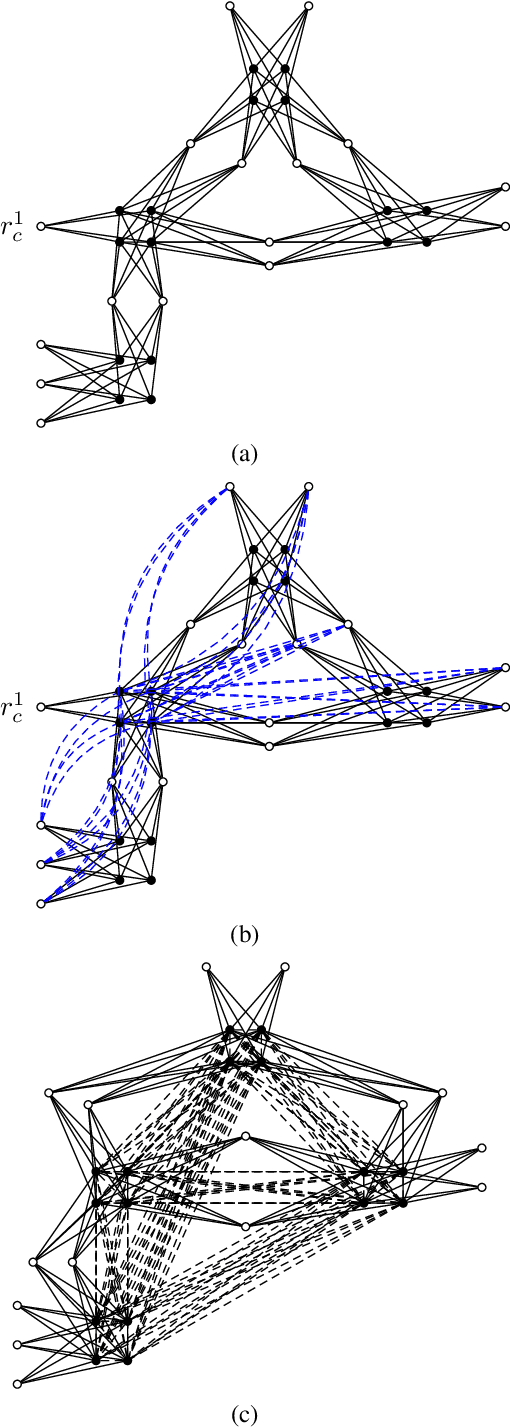
Moral graphs were introduced in the 1980s as an intermediate step when transforming a Bayesian network to a junction tree, on which exact belief propagation can be efficiently done. The moral graph of a Bayesian network can be trivially obtained by connecting non-adjacent parents for each node in the Bayesian network and dropping the direction of each edge. Perhaps because the moralization process looks simple, there has been little attention on the properties of moral graphs and their impact in belief propagation on Bayesian networks. This paper addresses the mistaken claim that it has been previously proved that optimal moral graph triangulation with the constraints of minimum fill-in, treewidth or total states is NP-complete. The problems are in fact NP-complete, but they have not previously been proved. We now prove these.

The Complexity of Morality: Checking Markov Blanket Consistency with DAGs via Morality

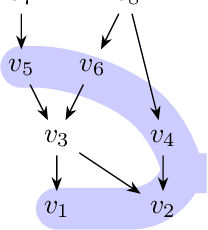
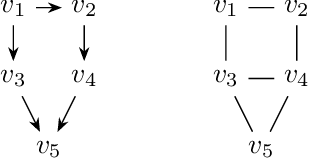
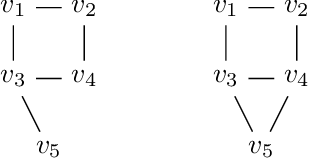
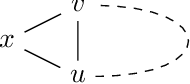
A family of Markov blankets in a faithful Bayesian network satisfies the symmetry and consistency properties. In this paper, we draw a bijection between families of consistent Markov blankets and moral graphs. We define the new concepts of weak recursive simpliciality and perfect elimination kits. We prove that they are equivalent to graph morality. In addition, we prove that morality can be decided in polynomial time for graphs with maximum degree less than $5$, but the problem is NP-complete for graphs with higher maximum degrees.

Minimum message length estimation of mixtures of multivariate Gaussian and von Mises-Fisher distributions

Mixture modelling involves explaining some observed evidence using a combination of probability distributions. The crux of the problem is the inference of an optimal number of mixture components and their corresponding parameters. This paper discusses unsupervised learning of mixture models using the Bayesian Minimum Message Length (MML) criterion. To demonstrate the effectiveness of search and inference of mixture parameters using the proposed approach, we select two key probability distributions, each handling fundamentally different types of data: the multivariate Gaussian distribution to address mixture modelling of data distributed in Euclidean space, and the multivariate von Mises-Fisher (vMF) distribution to address mixture modelling of directional data distributed on a unit hypersphere. The key contributions of this paper, in addition to the general search and inference methodology, include the derivation of MML expressions for encoding the data using multivariate Gaussian and von Mises-Fisher distributions, and the analytical derivation of the MML estimates of the parameters of the two distributions. Our approach is tested on simulated and real world data sets. For instance, we infer vMF mixtures that concisely explain experimentally determined three-dimensional protein conformations, providing an effective null model description of protein structures that is central to many inference problems in structural bioinformatics. The experimental results demonstrate that the performance of our proposed search and inference method along with the encoding schemes improve on the state of the art mixture modelling techniques.