Modelling Technical and Biological Effects in scRNA-seq data with Scalable GPLVMs

Single-cell RNA-seq datasets are growing in size and complexity, enabling the study of cellular composition changes in various biological/clinical contexts. Scalable dimensionality reduction techniques are in need to disentangle biological variation in them, while accounting for technical and biological confounders. In this work, we extend a popular approach for probabilistic non-linear dimensionality reduction, the Gaussian process latent variable model, to scale to massive single-cell datasets while explicitly accounting for technical and biological confounders. The key idea is to use an augmented kernel which preserves the factorisability of the lower bound allowing for fast stochastic variational inference. We demonstrate its ability to reconstruct latent signatures of innate immunity recovered in Kumasaka et al. (2021) with 9x lower training time. We further analyze a COVID dataset and demonstrate across a cohort of 130 individuals, that this framework enables data integration while capturing interpretable signatures of infection. Specifically, we explore COVID severity as a latent dimension to refine patient stratification and capture disease-specific gene expression.

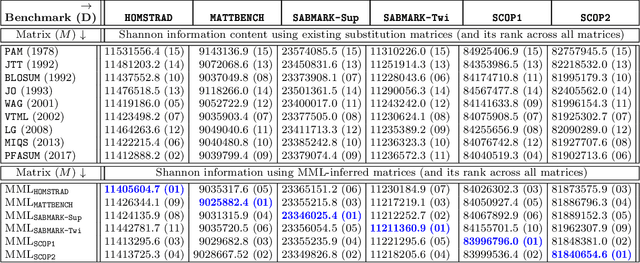
Bridging the Gaps in Statistical Models of Protein Alignment

This work demonstrates how a complete statistical model quantifying the evolution of pairs of aligned proteins can be constructed from a time-parameterised substitution matrix and a time-parameterised 3-state alignment machine. All parameters of such a model can be inferred from any benchmark data-set of aligned protein sequences. This allows us to examine nine well-known substitution matrices on six benchmarks curated using various structural alignment methods; any matrix that does not explicitly model a "time"-dependent Markov process is converted to a corresponding base-matrix that does. In addition, a new optimal matrix is inferred for each of the six benchmarks. Using Minimum Message Length (MML) inference, all 15 matrices are compared in terms of measuring the Shannon information content of each benchmark. This has resulted in a new and clear overall best performed time-dependent Markov matrix, MMLSUM, and its associated 3-state machine, whose properties we have analysed in this work. For standard use, the MMLSUM series of (log-odds) \textit{scoring} matrices derived from the above Markov matrix, are available at https://lcb.infotech.monash.edu.au/mmlsum.