The divergence time of protein structures modelled by Markov matrices and its relation to the divergence of sequences

A complete time-parameterized statistical model quantifying the divergent evolution of protein structures in terms of the patterns of conservation of their secondary structures is inferred from a large collection of protein 3D structure alignments. This provides a better alternative to time-parameterized sequence-based models of protein relatedness, that have clear limitations dealing with twilight and midnight zones of sequence relationships. Since protein structures are far more conserved due to the selection pressure directly placed on their function, divergence time estimates can be more accurate when inferred from structures. We use the Bayesian and information-theoretic framework of Minimum Message Length to infer a time-parameterized stochastic matrix (accounting for perturbed structural states of related residues) and associated Dirichlet models (accounting for insertions and deletions during the evolution of protein domains). These are used in concert to estimate the Markov time of divergence of tertiary structures, a task previously only possible using proxies (like RMSD). By analyzing one million pairs of homologous structures, we yield a relationship between the Markov divergence time of structures and of sequences. Using these inferred models and the relationship between the divergence of sequences and structures, we demonstrate a competitive performance in secondary structure prediction against neural network architectures commonly employed for this task. The source code and supplementary information are downloadable from \url{http://lcb.infotech.monash.edu.au/sstsum}.

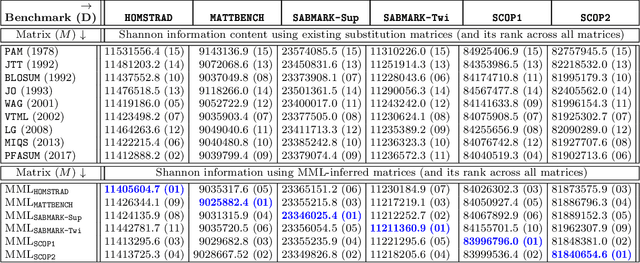
Bridging the Gaps in Statistical Models of Protein Alignment

This work demonstrates how a complete statistical model quantifying the evolution of pairs of aligned proteins can be constructed from a time-parameterised substitution matrix and a time-parameterised 3-state alignment machine. All parameters of such a model can be inferred from any benchmark data-set of aligned protein sequences. This allows us to examine nine well-known substitution matrices on six benchmarks curated using various structural alignment methods; any matrix that does not explicitly model a "time"-dependent Markov process is converted to a corresponding base-matrix that does. In addition, a new optimal matrix is inferred for each of the six benchmarks. Using Minimum Message Length (MML) inference, all 15 matrices are compared in terms of measuring the Shannon information content of each benchmark. This has resulted in a new and clear overall best performed time-dependent Markov matrix, MMLSUM, and its associated 3-state machine, whose properties we have analysed in this work. For standard use, the MMLSUM series of (log-odds) \textit{scoring} matrices derived from the above Markov matrix, are available at https://lcb.infotech.monash.edu.au/mmlsum.