Shared Stochastic Gaussian Process Latent Variable Models: A Multi-modal Generative Model for Quasar Spectra

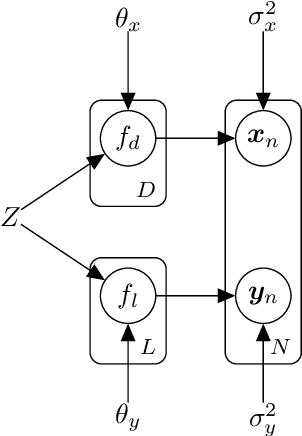
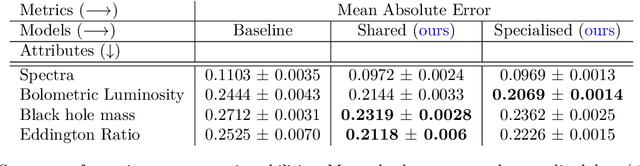
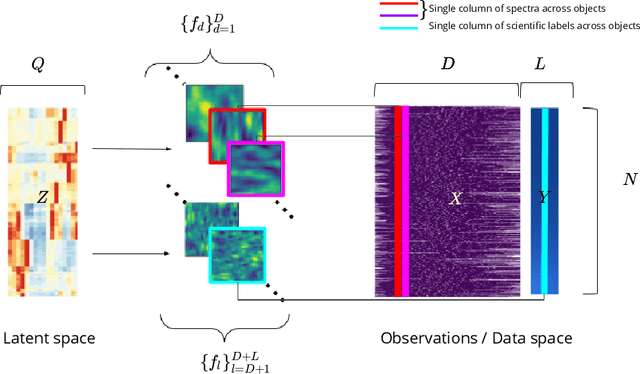
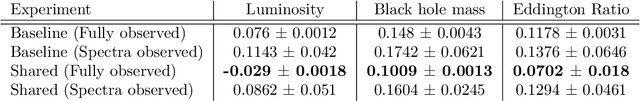
This work proposes a scalable probabilistic latent variable model based on Gaussian processes (Lawrence, 2004) in the context of multiple observation spaces. We focus on an application in astrophysics where data sets typically contain both observed spectral features and scientific properties of astrophysical objects such as galaxies or exoplanets. In our application, we study the spectra of very luminous galaxies known as quasars, along with their properties, such as the mass of their central supermassive black hole, accretion rate, and luminosity-resulting in multiple observation spaces. A single data point is then characterized by different classes of observations, each with different likelihoods. Our proposed model extends the baseline stochastic variational Gaussian process latent variable model (GPLVM) introduced by Lalchand et al. (2022) to this setting, proposing a seamless generative model where the quasar spectra and scientific labels can be generated simultaneously using a shared latent space as input to different sets of Gaussian process decoders, one for each observation space. Additionally, this framework enables training in a missing data setting where a large number of dimensions per data point may be unknown or unobserved. We demonstrate high-fidelity reconstructions of the spectra and scientific labels during test-time inference and briefly discuss the scientific interpretations of the results, along with the significance of such a generative model.

Permutation invariant multi-output Gaussian Processes for drug combination prediction in cancer

Dose-response prediction in cancer is an active application field in machine learning. Using large libraries of \textit{in-vitro} drug sensitivity screens, the goal is to develop accurate predictive models that can be used to guide experimental design or inform treatment decisions. Building on previous work that makes use of permutation invariant multi-output Gaussian Processes in the context of dose-response prediction for drug combinations, we develop a variational approximation to these models. The variational approximation enables a more scalable model that provides uncertainty quantification and naturally handles missing data. Furthermore, we propose using a deep generative model to encode the chemical space in a continuous manner, enabling prediction for new drugs and new combinations. We demonstrate the performance of our model in a simple setting using a high-throughput dataset and show that the model is able to efficiently borrow information across outputs.

Scalable Amortized GPLVMs for Single Cell Transcriptomics Data

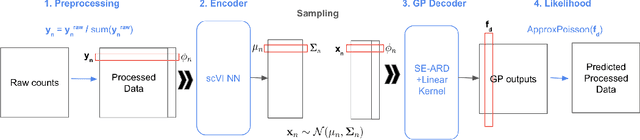
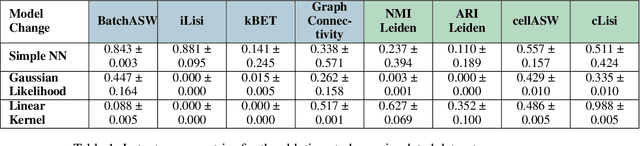
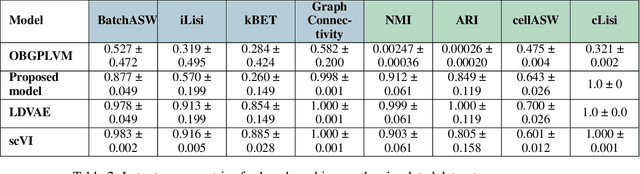
Dimensionality reduction is crucial for analyzing large-scale single-cell RNA-seq data. Gaussian Process Latent Variable Models (GPLVMs) offer an interpretable dimensionality reduction method, but current scalable models lack effectiveness in clustering cell types. We introduce an improved model, the amortized stochastic variational Bayesian GPLVM (BGPLVM), tailored for single-cell RNA-seq with specialized encoder, kernel, and likelihood designs. This model matches the performance of the leading single-cell variational inference (scVI) approach on synthetic and real-world COVID datasets and effectively incorporates cell-cycle and batch information to reveal more interpretable latent structures as we demonstrate on an innate immunity dataset.

Dimensionality Reduction as Probabilistic Inference

Dimensionality reduction (DR) algorithms compress high-dimensional data into a lower dimensional representation while preserving important features of the data. DR is a critical step in many analysis pipelines as it enables visualisation, noise reduction and efficient downstream processing of the data. In this work, we introduce the ProbDR variational framework, which interprets a wide range of classical DR algorithms as probabilistic inference algorithms in this framework. ProbDR encompasses PCA, CMDS, LLE, LE, MVU, diffusion maps, kPCA, Isomap, (t-)SNE, and UMAP. In our framework, a low-dimensional latent variable is used to construct a covariance, precision, or a graph Laplacian matrix, which can be used as part of a generative model for the data. Inference is done by optimizing an evidence lower bound. We demonstrate the internal consistency of our framework and show that it enables the use of probabilistic programming languages (PPLs) for DR. Additionally, we illustrate that the framework facilitates reasoning about unseen data and argue that our generative models approximate Gaussian processes (GPs) on manifolds. By providing a unified view of DR, our framework facilitates communication, reasoning about uncertainties, model composition, and extensions, particularly when domain knowledge is present.

Sparse Gaussian Process Hyperparameters: Optimize or Integrate?

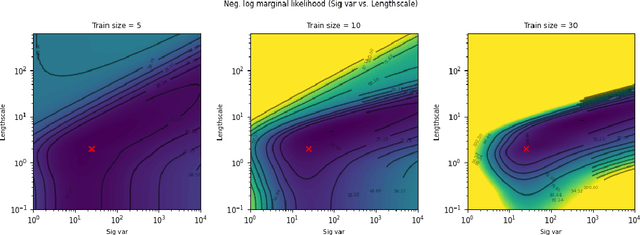
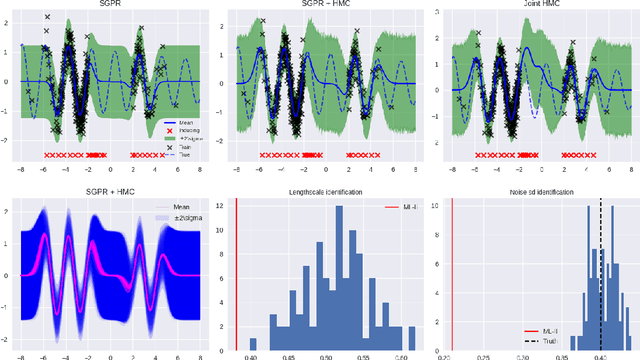
The kernel function and its hyperparameters are the central model selection choice in a Gaussian proces (Rasmussen and Williams, 2006). Typically, the hyperparameters of the kernel are chosen by maximising the marginal likelihood, an approach known as Type-II maximum likelihood (ML-II). However, ML-II does not account for hyperparameter uncertainty, and it is well-known that this can lead to severely biased estimates and an underestimation of predictive uncertainty. While there are several works which employ a fully Bayesian characterisation of GPs, relatively few propose such approaches for the sparse GPs paradigm. In this work we propose an algorithm for sparse Gaussian process regression which leverages MCMC to sample from the hyperparameter posterior within the variational inducing point framework of Titsias (2009). This work is closely related to Hensman et al. (2015b) but side-steps the need to sample the inducing points, thereby significantly improving sampling efficiency in the Gaussian likelihood case. We compare this scheme against natural baselines in literature along with stochastic variational GPs (SVGPs) along with an extensive computational analysis.

Modelling Technical and Biological Effects in scRNA-seq data with Scalable GPLVMs

Single-cell RNA-seq datasets are growing in size and complexity, enabling the study of cellular composition changes in various biological/clinical contexts. Scalable dimensionality reduction techniques are in need to disentangle biological variation in them, while accounting for technical and biological confounders. In this work, we extend a popular approach for probabilistic non-linear dimensionality reduction, the Gaussian process latent variable model, to scale to massive single-cell datasets while explicitly accounting for technical and biological confounders. The key idea is to use an augmented kernel which preserves the factorisability of the lower bound allowing for fast stochastic variational inference. We demonstrate its ability to reconstruct latent signatures of innate immunity recovered in Kumasaka et al. (2021) with 9x lower training time. We further analyze a COVID dataset and demonstrate across a cohort of 130 individuals, that this framework enables data integration while capturing interpretable signatures of infection. Specifically, we explore COVID severity as a latent dimension to refine patient stratification and capture disease-specific gene expression.

Kernel Learning for Explainable Climate Science

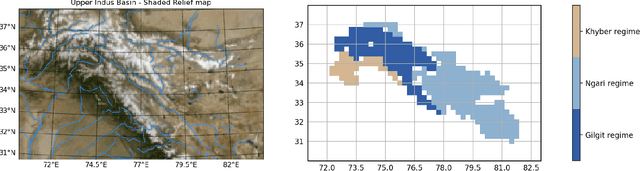
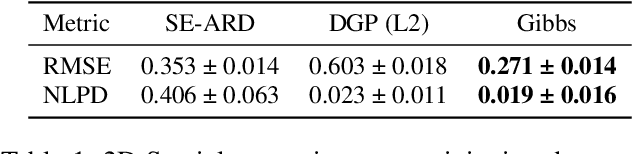
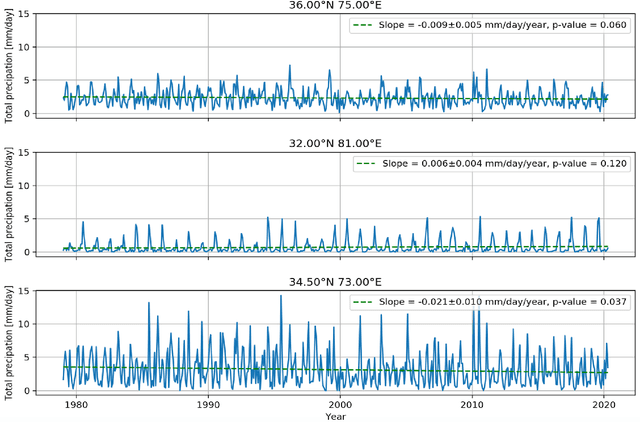
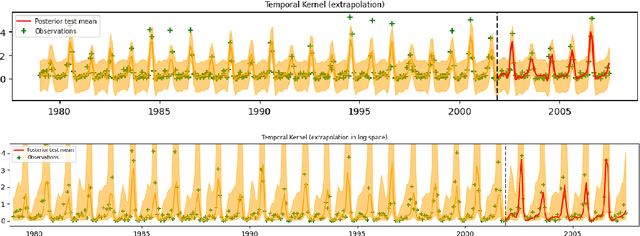
The Upper Indus Basin, Himalayas provides water for 270 million people and countless ecosystems. However, precipitation, a key component to hydrological modelling, is poorly understood in this area. A key challenge surrounding this uncertainty comes from the complex spatial-temporal distribution of precipitation across the basin. In this work we propose Gaussian processes with structured non-stationary kernels to model precipitation patterns in the UIB. Previous attempts to quantify or model precipitation in the Hindu Kush Karakoram Himalayan region have often been qualitative or include crude assumptions and simplifications which cannot be resolved at lower resolutions. This body of research also provides little to no error propagation. We account for the spatial variation in precipitation with a non-stationary Gibbs kernel parameterised with an input dependent lengthscale. This allows the posterior function samples to adapt to the varying precipitation patterns inherent in the distinct underlying topography of the Indus region. The input dependent lengthscale is governed by a latent Gaussian process with a stationary squared-exponential kernel to allow the function level hyperparameters to vary smoothly. In ablation experiments we motivate each component of the proposed kernel by demonstrating its ability to model the spatial covariance, temporal structure and joint spatio-temporal reconstruction. We benchmark our model with a stationary Gaussian process and a Deep Gaussian processes.

Generalised Gaussian Process Latent Variable Models (GPLVM) with Stochastic Variational Inference

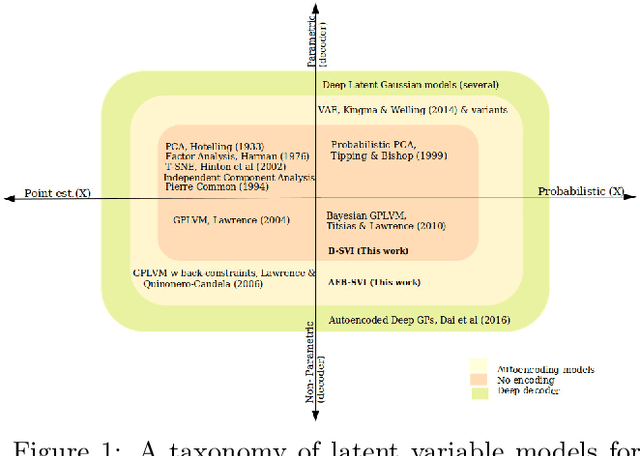
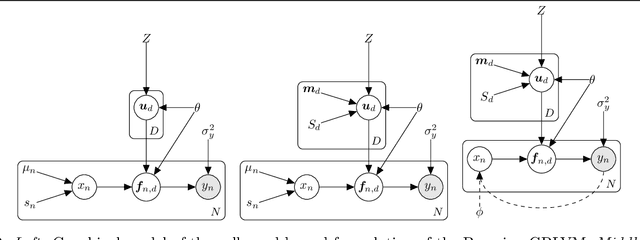
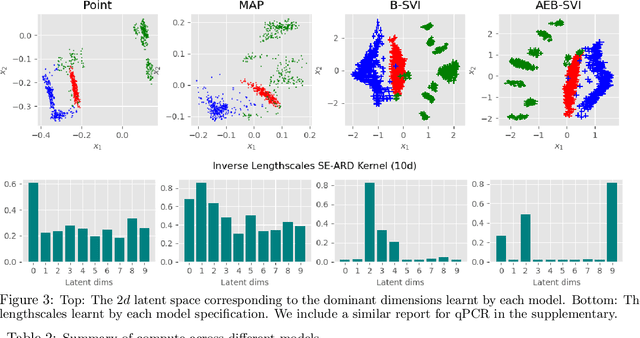
Gaussian process latent variable models (GPLVM) are a flexible and non-linear approach to dimensionality reduction, extending classical Gaussian processes to an unsupervised learning context. The Bayesian incarnation of the GPLVM Titsias and Lawrence, 2010] uses a variational framework, where the posterior over latent variables is approximated by a well-behaved variational family, a factorized Gaussian yielding a tractable lower bound. However, the non-factories ability of the lower bound prevents truly scalable inference. In this work, we study the doubly stochastic formulation of the Bayesian GPLVM model amenable with minibatch training. We show how this framework is compatible with different latent variable formulations and perform experiments to compare a suite of models. Further, we demonstrate how we can train in the presence of massively missing data and obtain high-fidelity reconstructions. We demonstrate the model's performance by benchmarking against the canonical sparse GPLVM for high-dimensional data examples.

Kernel Identification Through Transformers

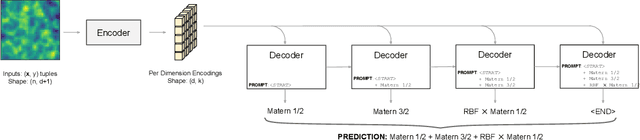
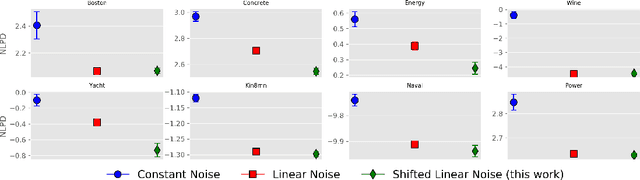
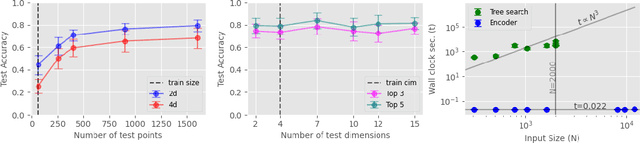
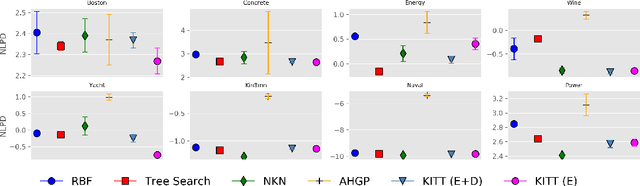
Kernel selection plays a central role in determining the performance of Gaussian Process (GP) models, as the chosen kernel determines both the inductive biases and prior support of functions under the GP prior. This work addresses the challenge of constructing custom kernel functions for high-dimensional GP regression models. Drawing inspiration from recent progress in deep learning, we introduce a novel approach named KITT: Kernel Identification Through Transformers. KITT exploits a transformer-based architecture to generate kernel recommendations in under 0.1 seconds, which is several orders of magnitude faster than conventional kernel search algorithms. We train our model using synthetic data generated from priors over a vocabulary of known kernels. By exploiting the nature of the self-attention mechanism, KITT is able to process datasets with inputs of arbitrary dimension. We demonstrate that kernels chosen by KITT yield strong performance over a diverse collection of regression benchmarks.

Marginalised Gaussian Processes with Nested Sampling

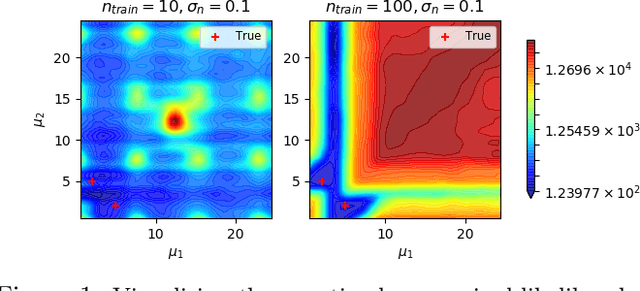
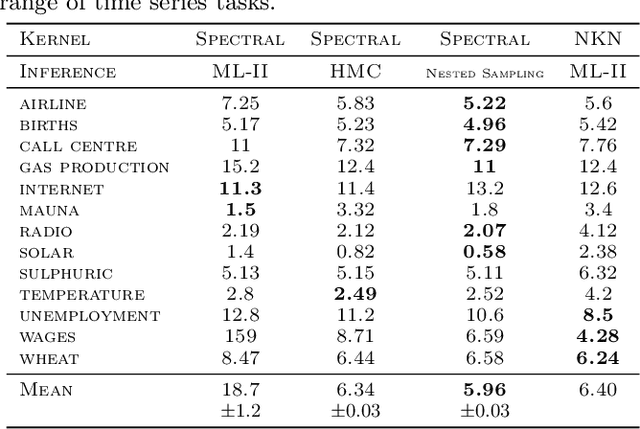
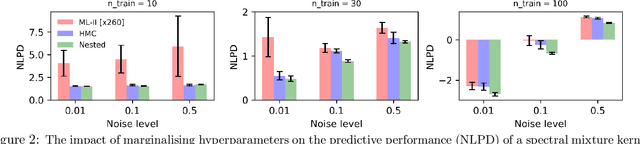
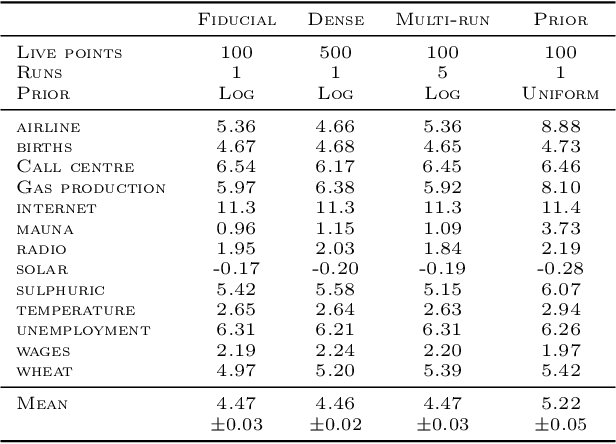
Gaussian Process (GPs) models are a rich distribution over functions with inductive biases controlled by a kernel function. Learning occurs through the optimisation of kernel hyperparameters using the marginal likelihood as the objective. This classical approach known as Type-II maximum likelihood (ML-II) yields point estimates of the hyperparameters, and continues to be the default method for training GPs. However, this approach risks underestimating predictive uncertainty and is prone to overfitting especially when there are many hyperparameters. Furthermore, gradient based optimisation makes ML-II point estimates highly susceptible to the presence of local minima. This work presents an alternative learning procedure where the hyperparameters of the kernel function are marginalised using Nested Sampling (NS), a technique that is well suited to sample from complex, multi-modal distributions. We focus on regression tasks with the spectral mixture (SM) class of kernels and find that a principled approach to quantifying model uncertainty leads to substantial gains in predictive performance across a range of synthetic and benchmark data sets. In this context, nested sampling is also found to offer a speed advantage over Hamiltonian Monte Carlo (HMC), widely considered to be the gold-standard in MCMC based inference.