Sparse Gaussian Process Hyperparameters: Optimize or Integrate?

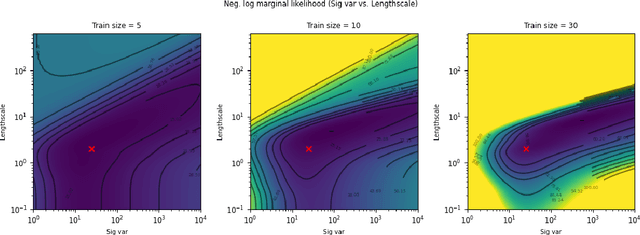
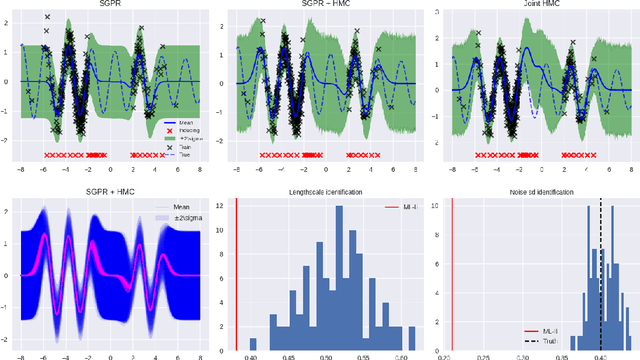
The kernel function and its hyperparameters are the central model selection choice in a Gaussian proces (Rasmussen and Williams, 2006). Typically, the hyperparameters of the kernel are chosen by maximising the marginal likelihood, an approach known as Type-II maximum likelihood (ML-II). However, ML-II does not account for hyperparameter uncertainty, and it is well-known that this can lead to severely biased estimates and an underestimation of predictive uncertainty. While there are several works which employ a fully Bayesian characterisation of GPs, relatively few propose such approaches for the sparse GPs paradigm. In this work we propose an algorithm for sparse Gaussian process regression which leverages MCMC to sample from the hyperparameter posterior within the variational inducing point framework of Titsias (2009). This work is closely related to Hensman et al. (2015b) but side-steps the need to sample the inducing points, thereby significantly improving sampling efficiency in the Gaussian likelihood case. We compare this scheme against natural baselines in literature along with stochastic variational GPs (SVGPs) along with an extensive computational analysis.

The Promises and Pitfalls of Deep Kernel Learning

Deep kernel learning and related techniques promise to combine the representational power of neural networks with the reliable uncertainty estimates of Gaussian processes. One crucial aspect of these models is an expectation that, because they are treated as Gaussian process models optimized using the marginal likelihood, they are protected from overfitting. However, we identify pathological behavior, including overfitting, on a simple toy example. We explore this pathology, explaining its origins and considering how it applies to real datasets. Through careful experimentation on UCI datasets, CIFAR-10, and the UTKFace dataset, we find that the overfitting from overparameterized deep kernel learning, in which the model is "somewhat Bayesian", can in certain scenarios be worse than that from not being Bayesian at all. However, we find that a fully Bayesian treatment of deep kernel learning can rectify this overfitting and obtain the desired performance improvements over standard neural networks and Gaussian processes.

Deep Structured Mixtures of Gaussian Processes

Gaussian Processes (GPs) are powerful non-parametric Bayesian regression models that allow exact posterior inference, but exhibit high computational and memory costs. In order to improve scalability of GPs, approximate posterior inference is frequently employed, where a prominent class of approximation techniques is based on local GP experts. However, the local-expert techniques proposed so far are either not well-principled, come with limited approximation guarantees, or lead to intractable models. In this paper, we introduce deep structured mixtures of GP experts, a stochastic process model which i) allows exact posterior inference, ii) has attractive computational and memory costs, and iii), when used as GP approximation, captures predictive uncertainties consistently better than previous approximations. In a variety of experiments, we show that deep structured mixtures have a low approximation error and outperform existing expert-based approaches.

Rates of Convergence for Sparse Variational Gaussian Process Regression

Excellent variational approximations to Gaussian process posteriors have been developed which avoid the $\mathcal{O}\left(N^3\right)$ scaling with dataset size $N$. They reduce the computational cost to $\mathcal{O}\left(NM^2\right)$, with $M\ll N$ being the number of inducing variables, which summarise the process. While the computational cost seems to be linear in $N$, the true complexity of the algorithm depends on how $M$ must increase to ensure a certain quality of approximation. We address this by characterising the behavior of an upper bound on the KL divergence to the posterior. We show that with high probability the KL divergence can be made arbitrarily small by growing $M$ more slowly than $N$. A particular case of interest is that for regression with normally distributed inputs in D-dimensions with the popular Squared Exponential kernel, $M=\mathcal{O}(\log^D N)$ is sufficient. Our results show that as datasets grow, Gaussian process posteriors can truly be approximated cheaply, and provide a concrete rule for how to increase $M$ in continual learning scenarios.

Learning Deep Mixtures of Gaussian Process Experts Using Sum-Product Networks

While Gaussian processes (GPs) are the method of choice for regression tasks, they also come with practical difficulties, as inference cost scales cubic in time and quadratic in memory. In this paper, we introduce a natural and expressive way to tackle these problems, by incorporating GPs in sum-product networks (SPNs), a recently proposed tractable probabilistic model allowing exact and efficient inference. In particular, by using GPs as leaves of an SPN we obtain a novel flexible prior over functions, which implicitly represents an exponentially large mixture of local GPs. Exact and efficient posterior inference in this model can be done in a natural interplay of the inference mechanisms in GPs and SPNs. Thereby, each GP is -- similarly as in a mixture of experts approach -- responsible only for a subset of data points, which effectively reduces inference cost in a divide and conquer fashion. We show that integrating GPs into the SPN framework leads to a promising probabilistic regression model which is: (1) computational and memory efficient, (2) allows efficient and exact posterior inference, (3) is flexible enough to mix different kernel functions, and (4) naturally accounts for non-stationarities in time series. In a variate of experiments, we show that the SPN-GP model can learn input dependent parameters and hyper-parameters and is on par with or outperforms the traditional GPs as well as state of the art approximations on real-world data.

Variational Gaussian Process State-Space Models

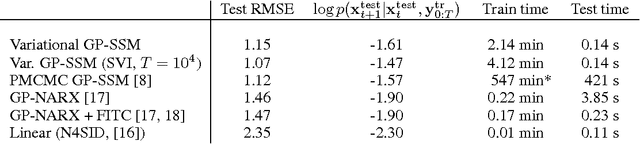
State-space models have been successfully used for more than fifty years in different areas of science and engineering. We present a procedure for efficient variational Bayesian learning of nonlinear state-space models based on sparse Gaussian processes. The result of learning is a tractable posterior over nonlinear dynamical systems. In comparison to conventional parametric models, we offer the possibility to straightforwardly trade off model capacity and computational cost whilst avoiding overfitting. Our main algorithm uses a hybrid inference approach combining variational Bayes and sequential Monte Carlo. We also present stochastic variational inference and online learning approaches for fast learning with long time series.

Distributed Variational Inference in Sparse Gaussian Process Regression and Latent Variable Models

Gaussian processes (GPs) are a powerful tool for probabilistic inference over functions. They have been applied to both regression and non-linear dimensionality reduction, and offer desirable properties such as uncertainty estimates, robustness to over-fitting, and principled ways for tuning hyper-parameters. However the scalability of these models to big datasets remains an active topic of research. We introduce a novel re-parametrisation of variational inference for sparse GP regression and latent variable models that allows for an efficient distributed algorithm. This is done by exploiting the decoupling of the data given the inducing points to re-formulate the evidence lower bound in a Map-Reduce setting. We show that the inference scales well with data and computational resources, while preserving a balanced distribution of the load among the nodes. We further demonstrate the utility in scaling Gaussian processes to big data. We show that GP performance improves with increasing amounts of data in regression (on flight data with 2 million records) and latent variable modelling (on MNIST). The results show that GPs perform better than many common models often used for big data.

Identification of Gaussian Process State-Space Models with Particle Stochastic Approximation EM

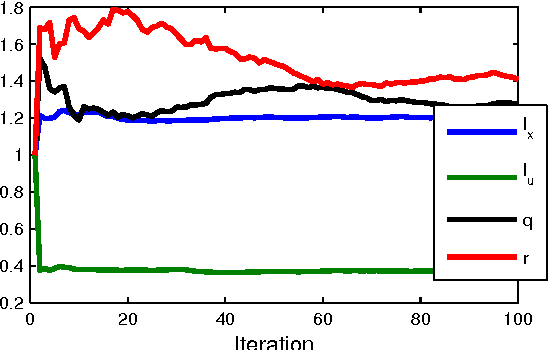
Gaussian process state-space models (GP-SSMs) are a very flexible family of models of nonlinear dynamical systems. They comprise a Bayesian nonparametric representation of the dynamics of the system and additional (hyper-)parameters governing the properties of this nonparametric representation. The Bayesian formalism enables systematic reasoning about the uncertainty in the system dynamics. We present an approach to maximum likelihood identification of the parameters in GP-SSMs, while retaining the full nonparametric description of the dynamics. The method is based on a stochastic approximation version of the EM algorithm that employs recent developments in particle Markov chain Monte Carlo for efficient identification.

Bayesian Inference and Learning in Gaussian Process State-Space Models with Particle MCMC

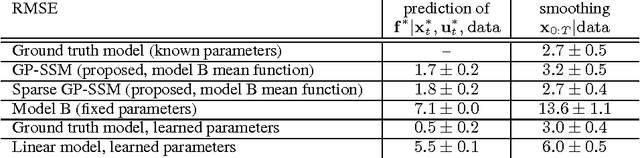
State-space models are successfully used in many areas of science, engineering and economics to model time series and dynamical systems. We present a fully Bayesian approach to inference \emph{and learning} (i.e. state estimation and system identification) in nonlinear nonparametric state-space models. We place a Gaussian process prior over the state transition dynamics, resulting in a flexible model able to capture complex dynamical phenomena. To enable efficient inference, we marginalize over the transition dynamics function and infer directly the joint smoothing distribution using specially tailored Particle Markov Chain Monte Carlo samplers. Once a sample from the smoothing distribution is computed, the state transition predictive distribution can be formulated analytically. Our approach preserves the full nonparametric expressivity of the model and can make use of sparse Gaussian processes to greatly reduce computational complexity.