Variational Gaussian Process State-Space Models
Paper and Code
Nov 03, 2014
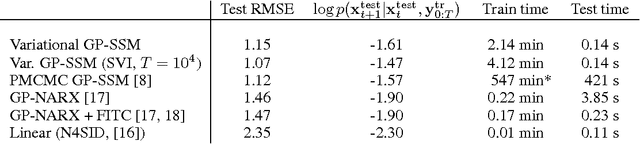


State-space models have been successfully used for more than fifty years in different areas of science and engineering. We present a procedure for efficient variational Bayesian learning of nonlinear state-space models based on sparse Gaussian processes. The result of learning is a tractable posterior over nonlinear dynamical systems. In comparison to conventional parametric models, we offer the possibility to straightforwardly trade off model capacity and computational cost whilst avoiding overfitting. Our main algorithm uses a hybrid inference approach combining variational Bayes and sequential Monte Carlo. We also present stochastic variational inference and online learning approaches for fast learning with long time series.
* R. Frigola, Y. Chen and C. E. Rasmussen. Variational Gaussian
Process State-Space Models, in Advances in Neural Information Processing
Systems (NIPS), 2014
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge