Variational Gaussian Process State-Space Models

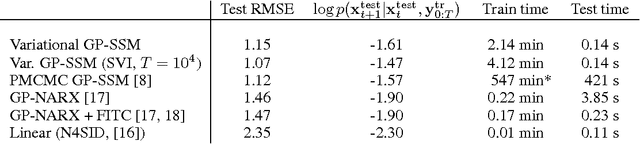
State-space models have been successfully used for more than fifty years in different areas of science and engineering. We present a procedure for efficient variational Bayesian learning of nonlinear state-space models based on sparse Gaussian processes. The result of learning is a tractable posterior over nonlinear dynamical systems. In comparison to conventional parametric models, we offer the possibility to straightforwardly trade off model capacity and computational cost whilst avoiding overfitting. Our main algorithm uses a hybrid inference approach combining variational Bayes and sequential Monte Carlo. We also present stochastic variational inference and online learning approaches for fast learning with long time series.

Identification of Gaussian Process State-Space Models with Particle Stochastic Approximation EM

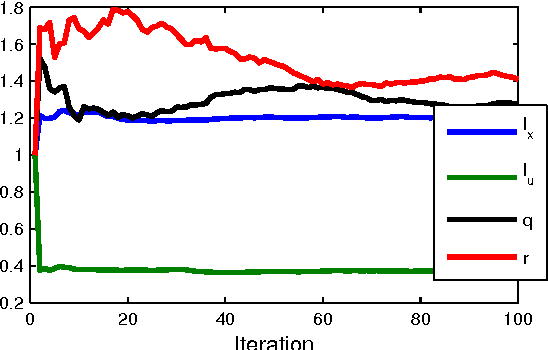
Gaussian process state-space models (GP-SSMs) are a very flexible family of models of nonlinear dynamical systems. They comprise a Bayesian nonparametric representation of the dynamics of the system and additional (hyper-)parameters governing the properties of this nonparametric representation. The Bayesian formalism enables systematic reasoning about the uncertainty in the system dynamics. We present an approach to maximum likelihood identification of the parameters in GP-SSMs, while retaining the full nonparametric description of the dynamics. The method is based on a stochastic approximation version of the EM algorithm that employs recent developments in particle Markov chain Monte Carlo for efficient identification.

Bayesian Inference and Learning in Gaussian Process State-Space Models with Particle MCMC

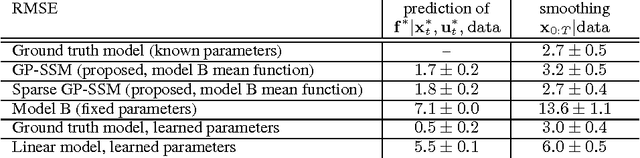
State-space models are successfully used in many areas of science, engineering and economics to model time series and dynamical systems. We present a fully Bayesian approach to inference \emph{and learning} (i.e. state estimation and system identification) in nonlinear nonparametric state-space models. We place a Gaussian process prior over the state transition dynamics, resulting in a flexible model able to capture complex dynamical phenomena. To enable efficient inference, we marginalize over the transition dynamics function and infer directly the joint smoothing distribution using specially tailored Particle Markov Chain Monte Carlo samplers. Once a sample from the smoothing distribution is computed, the state transition predictive distribution can be formulated analytically. Our approach preserves the full nonparametric expressivity of the model and can make use of sparse Gaussian processes to greatly reduce computational complexity.

Integrated Pre-Processing for Bayesian Nonlinear System Identification with Gaussian Processes

We introduce GP-FNARX: a new model for nonlinear system identification based on a nonlinear autoregressive exogenous model (NARX) with filtered regressors (F) where the nonlinear regression problem is tackled using sparse Gaussian processes (GP). We integrate data pre-processing with system identification into a fully automated procedure that goes from raw data to an identified model. Both pre-processing parameters and GP hyper-parameters are tuned by maximizing the marginal likelihood of the probabilistic model. We obtain a Bayesian model of the system's dynamics which is able to report its uncertainty in regions where the data is scarce. The automated approach, the modeling of uncertainty and its relatively low computational cost make of GP-FNARX a good candidate for applications in robotics and adaptive control.