Exact Soft Analytical Side-Channel Attacks using Tractable Circuits

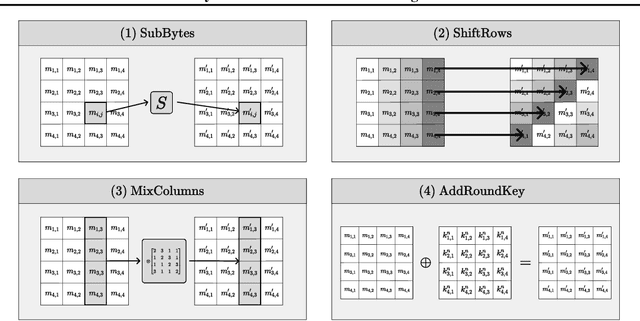
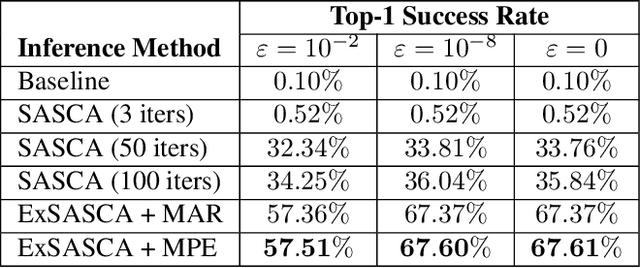
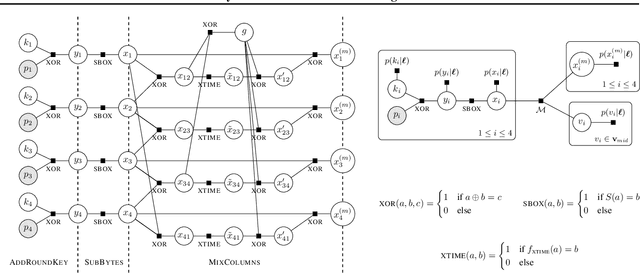
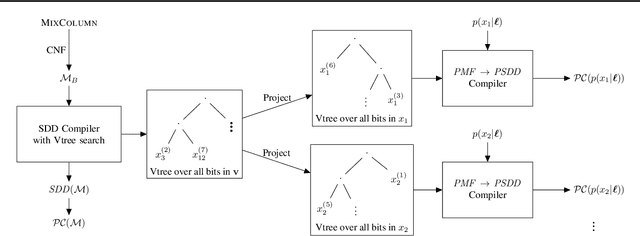
Detecting weaknesses in cryptographic algorithms is of utmost importance for designing secure information systems. The state-of-the-art soft analytical side-channel attack (SASCA) uses physical leakage information to make probabilistic predictions about intermediate computations and combines these "guesses" with the known algorithmic logic to compute the posterior distribution over the key. This attack is commonly performed via loopy belief propagation, which, however, lacks guarantees in terms of convergence and inference quality. In this paper, we develop a fast and exact inference method for SASCA, denoted as ExSASCA, by leveraging knowledge compilation and tractable probabilistic circuits. When attacking the Advanced Encryption Standard (AES), the most widely used encryption algorithm to date, ExSASCA outperforms SASCA by more than 31% top-1 success rate absolute. By leveraging sparse belief messages, this performance is achieved with little more computational cost than SASCA, and about 3 orders of magnitude less than exact inference via exhaustive enumeration. Even with dense belief messages, ExSASCA still uses 6 times less computations than exhaustive inference.

What is the Relationship between Tensor Factorizations and Circuits (and How Can We Exploit it)?

This paper establishes a rigorous connection between circuit representations and tensor factorizations, two seemingly distinct yet fundamentally related areas. By connecting these fields, we highlight a series of opportunities that can benefit both communities. Our work generalizes popular tensor factorizations within the circuit language, and unifies various circuit learning algorithms under a single, generalized hierarchical factorization framework. Specifically, we introduce a modular "Lego block" approach to build tensorized circuit architectures. This, in turn, allows us to systematically construct and explore various circuit and tensor factorization models while maintaining tractability. This connection not only clarifies similarities and differences in existing models, but also enables the development of a comprehensive pipeline for building and optimizing new circuit/tensor factorization architectures. We show the effectiveness of our framework through extensive empirical evaluations, and highlight new research opportunities for tensor factorizations in probabilistic modeling.

One-Shot Federated Learning with Bayesian Pseudocoresets

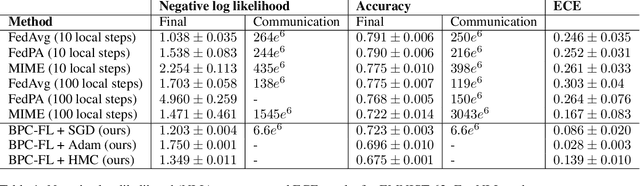
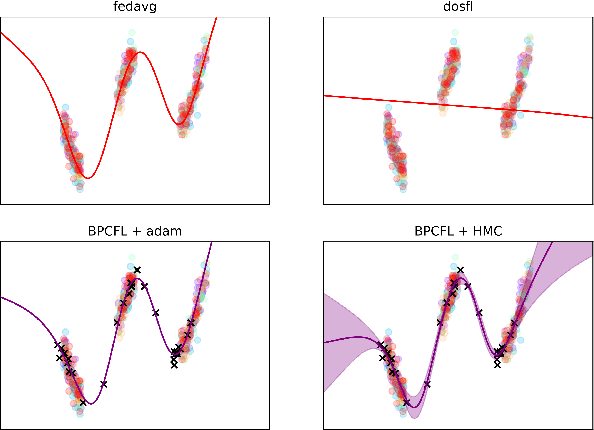
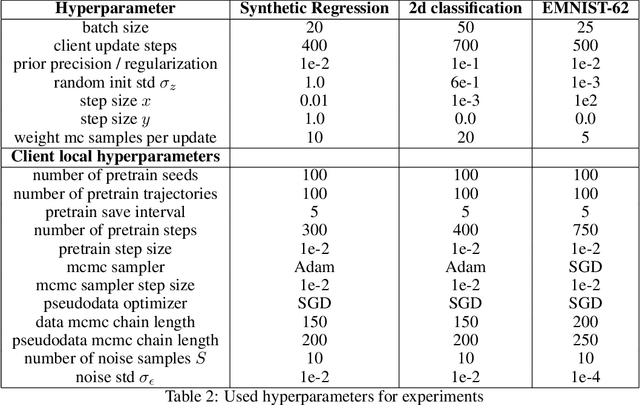
Optimization-based techniques for federated learning (FL) often come with prohibitive communication cost, as high dimensional model parameters need to be communicated repeatedly between server and clients. In this paper, we follow a Bayesian approach allowing to perform FL with one-shot communication, by solving the global inference problem as a product of local client posteriors. For models with multi-modal likelihoods, such as neural networks, a naive application of this scheme is hampered, since clients will capture different posterior modes, causing a destructive collapse of the posterior on the server side. Consequently, we explore approximate inference in the function-space representation of client posteriors, hence suffering less or not at all from multi-modality. We show that distributed function-space inference is tightly related to learning Bayesian pseudocoresets and develop a tractable Bayesian FL algorithm on this insight. We show that this approach achieves prediction performance competitive to state-of-the-art while showing a striking reduction in communication cost of up to two orders of magnitude. Moreover, due to its Bayesian nature, our method also delivers well-calibrated uncertainty estimates.

Rao-Blackwellising Bayesian Causal Inference

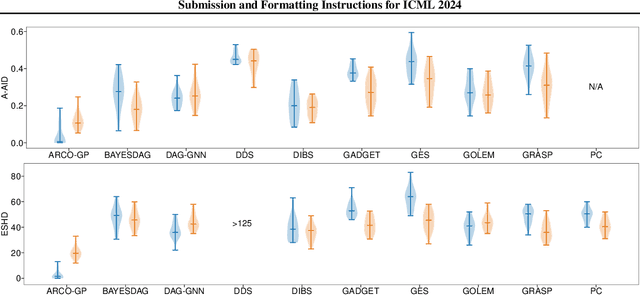
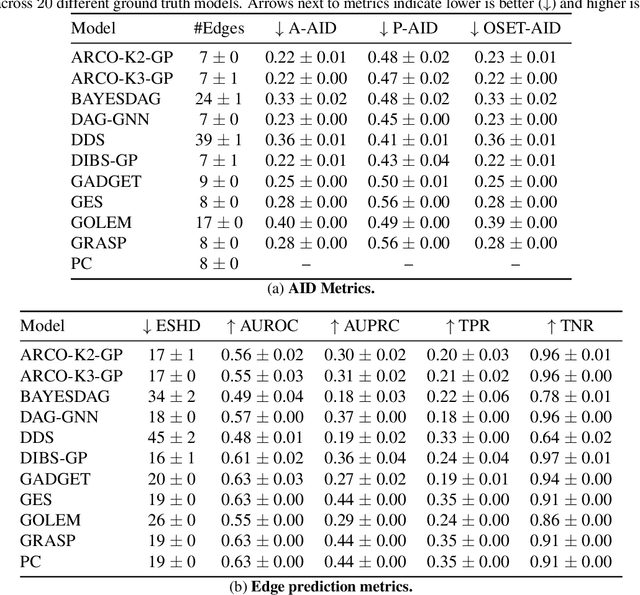
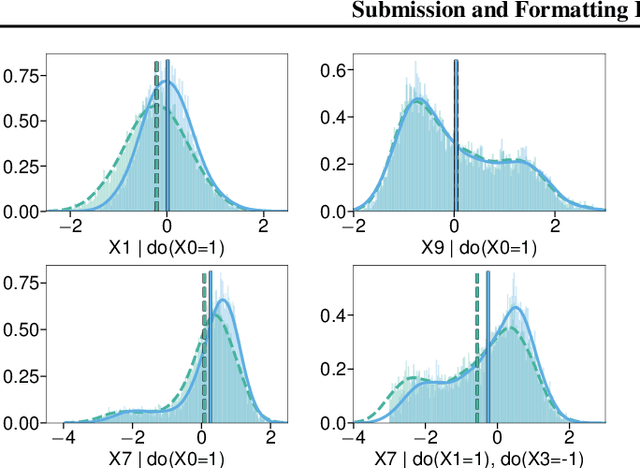
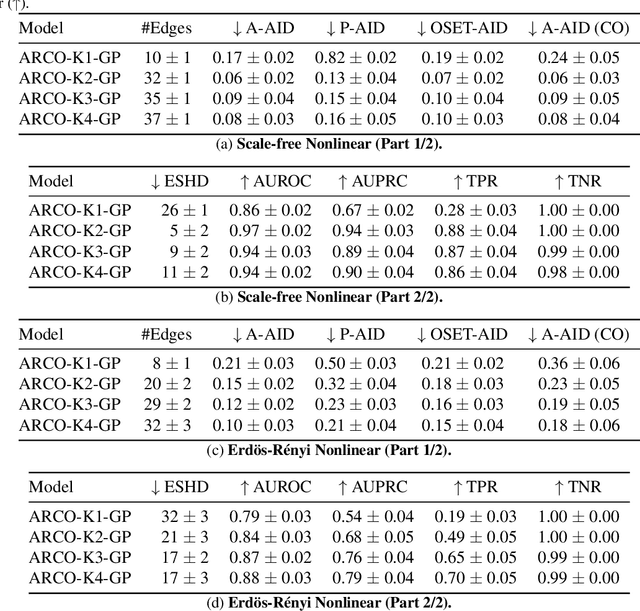
Bayesian causal inference, i.e., inferring a posterior over causal models for the use in downstream causal reasoning tasks, poses a hard computational inference problem that is little explored in literature. In this work, we combine techniques from order-based MCMC structure learning with recent advances in gradient-based graph learning into an effective Bayesian causal inference framework. Specifically, we decompose the problem of inferring the causal structure into (i) inferring a topological order over variables and (ii) inferring the parent sets for each variable. When limiting the number of parents per variable, we can exactly marginalise over the parent sets in polynomial time. We further use Gaussian processes to model the unknown causal mechanisms, which also allows their exact marginalisation. This introduces a Rao-Blackwellization scheme, where all components are eliminated from the model, except for the causal order, for which we learn a distribution via gradient-based optimisation. The combination of Rao-Blackwellization with our sequential inference procedure for causal orders yields state-of-the-art on linear and non-linear additive noise benchmarks with scale-free and Erdos-Renyi graph structures.

Probabilistic Integral Circuits

Continuous latent variables (LVs) are a key ingredient of many generative models, as they allow modelling expressive mixtures with an uncountable number of components. In contrast, probabilistic circuits (PCs) are hierarchical discrete mixtures represented as computational graphs composed of input, sum and product units. Unlike continuous LV models, PCs provide tractable inference but are limited to discrete LVs with categorical (i.e. unordered) states. We bridge these model classes by introducing probabilistic integral circuits (PICs), a new language of computational graphs that extends PCs with integral units representing continuous LVs. In the first place, PICs are symbolic computational graphs and are fully tractable in simple cases where analytical integration is possible. In practice, we parameterise PICs with light-weight neural nets delivering an intractable hierarchical continuous mixture that can be approximated arbitrarily well with large PCs using numerical quadrature. On several distribution estimation benchmarks, we show that such PIC-approximating PCs systematically outperform PCs commonly learned via expectation-maximization or SGD.

How to Turn Your Knowledge Graph Embeddings into Generative Models via Probabilistic Circuits

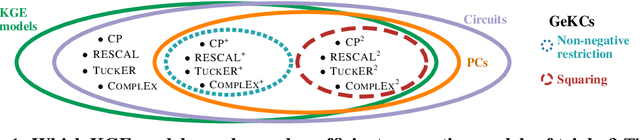
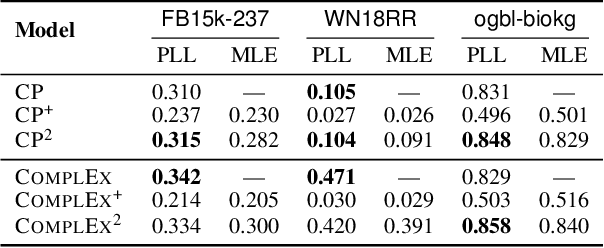
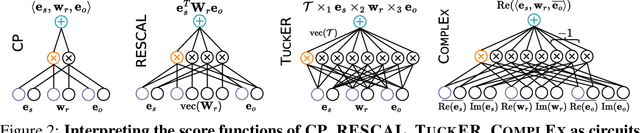
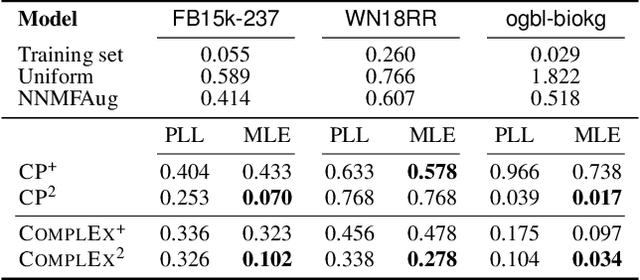
Some of the most successful knowledge graph embedding (KGE) models for link prediction -- CP, RESCAL, TuckER, ComplEx -- can be interpreted as energy-based models. Under this perspective they are not amenable for exact maximum-likelihood estimation (MLE), sampling and struggle to integrate logical constraints. This work re-interprets the score functions of these KGEs as circuits -- constrained computational graphs allowing efficient marginalisation. Then, we design two recipes to obtain efficient generative circuit models by either restricting their activations to be non-negative or squaring their outputs. Our interpretation comes with little or no loss of performance for link prediction, while the circuits framework unlocks exact learning by MLE, efficient sampling of new triples, and guarantee that logical constraints are satisfied by design. Furthermore, our models scale more gracefully than the original KGEs on graphs with millions of entities.

Bayesian Structure Scores for Probabilistic Circuits

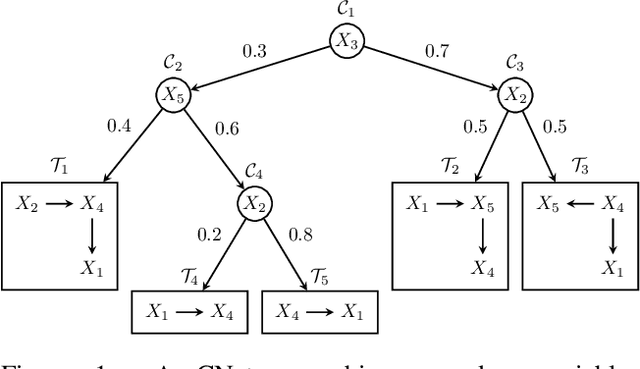
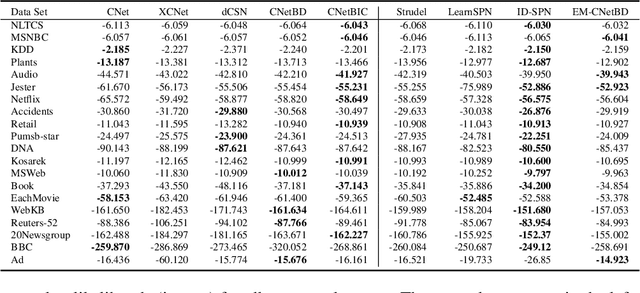
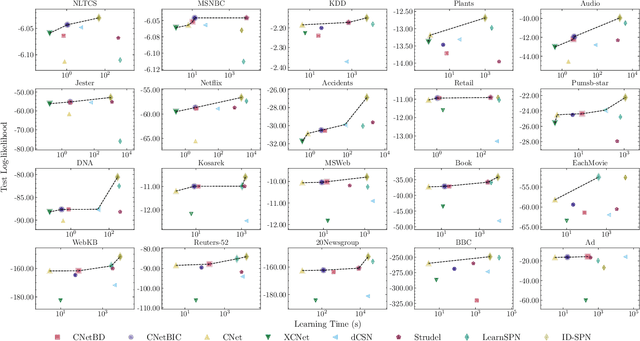
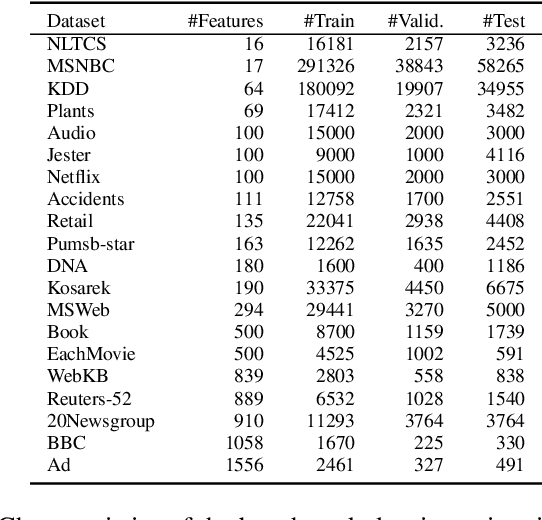
Probabilistic circuits (PCs) are a prominent representation of probability distributions with tractable inference. While parameter learning in PCs is rigorously studied, structure learning is often more based on heuristics than on principled objectives. In this paper, we develop Bayesian structure scores for deterministic PCs, i.e., the structure likelihood with parameters marginalized out, which are well known as rigorous objectives for structure learning in probabilistic graphical models. When used within a greedy cutset algorithm, our scores effectively protect against overfitting and yield a fast and almost hyper-parameter-free structure learner, distinguishing it from previous approaches. In experiments, we achieve good trade-offs between training time and model fit in terms of log-likelihood. Moreover, the principled nature of Bayesian scores unlocks PCs for accommodating frameworks such as structural expectation-maximization.

Continuous Mixtures of Tractable Probabilistic Models

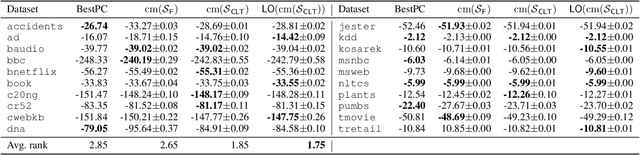
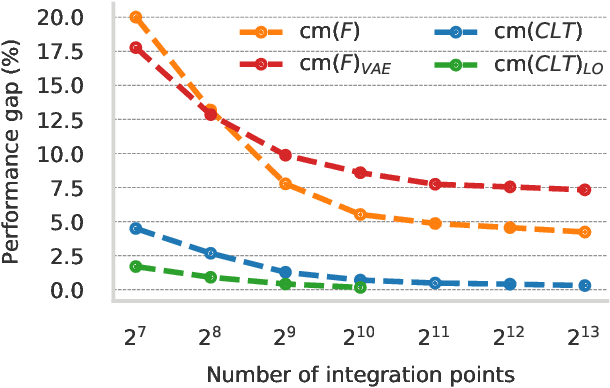
Probabilistic models based on continuous latent spaces, such as variational autoencoders, can be understood as uncountable mixture models where components depend continuously on the latent code. They have proven expressive tools for generative and probabilistic modelling, but are at odds with tractable probabilistic inference, that is, computing marginals and conditionals of the represented probability distribution. Meanwhile, tractable probabilistic models such as probabilistic circuits (PCs) can be understood as hierarchical discrete mixture models, which allows them to perform exact inference, but often they show subpar performance in comparison to continuous latent-space models. In this paper, we investigate a hybrid approach, namely continuous mixtures of tractable models with a small latent dimension. While these models are analytically intractable, they are well amenable to numerical integration schemes based on a finite set of integration points. With a large enough number of integration points the approximation becomes de-facto exact. Moreover, using a finite set of integration points, the approximation method can be compiled into a PC performing `exact inference in an approximate model'. In experiments, we show that this simple scheme proves remarkably effective, as PCs learned this way set new state-of-the-art for tractable models on many standard density estimation benchmarks.

Active Bayesian Causal Inference

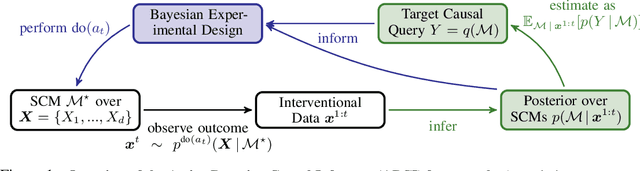
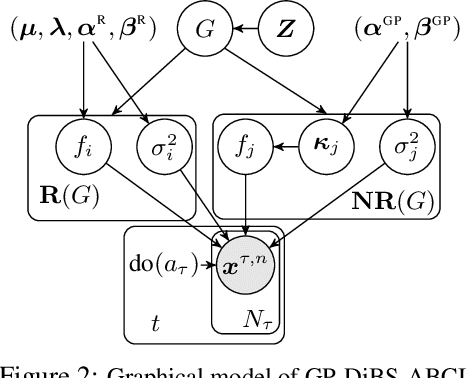
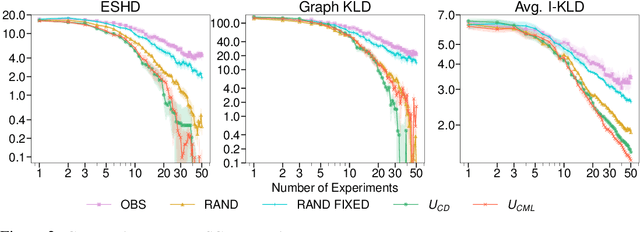
Causal discovery and causal reasoning are classically treated as separate and consecutive tasks: one first infers the causal graph, and then uses it to estimate causal effects of interventions. However, such a two-stage approach is uneconomical, especially in terms of actively collected interventional data, since the causal query of interest may not require a fully-specified causal model. From a Bayesian perspective, it is also unnatural, since a causal query (e.g., the causal graph or some causal effect) can be viewed as a latent quantity subject to posterior inference -- other unobserved quantities that are not of direct interest (e.g., the full causal model) ought to be marginalized out in this process and contribute to our epistemic uncertainty. In this work, we propose Active Bayesian Causal Inference (ABCI), a fully-Bayesian active learning framework for integrated causal discovery and reasoning, which jointly infers a posterior over causal models and queries of interest. In our approach to ABCI, we focus on the class of causally-sufficient, nonlinear additive noise models, which we model using Gaussian processes. We sequentially design experiments that are maximally informative about our target causal query, collect the corresponding interventional data, and update our beliefs to choose the next experiment. Through simulations, we demonstrate that our approach is more data-efficient than several baselines that only focus on learning the full causal graph. This allows us to accurately learn downstream causal queries from fewer samples while providing well-calibrated uncertainty estimates for the quantities of interest.

Joints in Random Forests

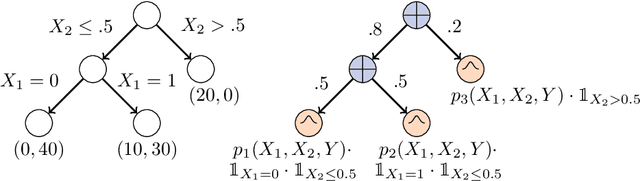
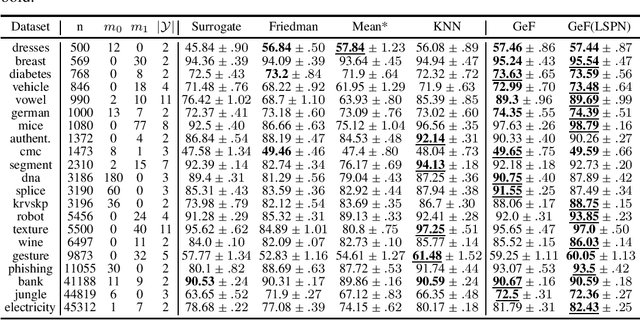
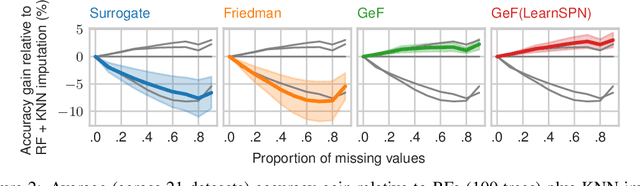
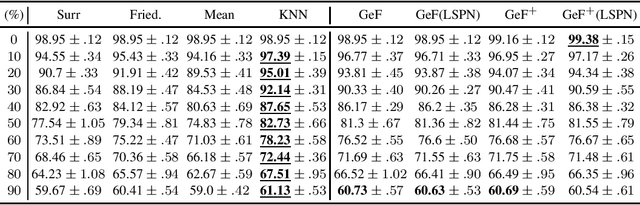
Decision Trees (DTs) and Random Forests (RFs) are powerful discriminative learners and tools of central importance to the everyday machine learning practitioner and data scientist. Due to their discriminative nature, however, they lack principled methods to process inputs with missing features or to detect outliers, which requires pairing them with imputation techniques or a separate generative model. In this paper, we demonstrate that DTs and RFs can naturally be interpreted as generative models, by drawing a connection to Probabilistic Circuits, a prominent class of tractable probabilistic models. This reinterpretation equips them with a full joint distribution over the feature space and leads to Generative Decision Trees (GeDTs) and Generative Forests (GeFs), a family of novel hybrid generative-discriminative models. This family of models retains the overall characteristics of DTs and RFs while additionally being able to handle missing features by means of marginalisation. Under certain assumptions, frequently made for Bayes consistency results, we show that consistency in GeDTs and GeFs extend to any pattern of missing input features, if missing at random. Empirically, we show that our models often outperform common routines to treat missing data, such as K-nearest neighbour imputation, and moreover, that our models can naturally detect outliers by monitoring the marginal probability of input features.