What is the Relationship between Tensor Factorizations and Circuits (and How Can We Exploit it)?

This paper establishes a rigorous connection between circuit representations and tensor factorizations, two seemingly distinct yet fundamentally related areas. By connecting these fields, we highlight a series of opportunities that can benefit both communities. Our work generalizes popular tensor factorizations within the circuit language, and unifies various circuit learning algorithms under a single, generalized hierarchical factorization framework. Specifically, we introduce a modular "Lego block" approach to build tensorized circuit architectures. This, in turn, allows us to systematically construct and explore various circuit and tensor factorization models while maintaining tractability. This connection not only clarifies similarities and differences in existing models, but also enables the development of a comprehensive pipeline for building and optimizing new circuit/tensor factorization architectures. We show the effectiveness of our framework through extensive empirical evaluations, and highlight new research opportunities for tensor factorizations in probabilistic modeling.

Nerva: a Truly Sparse Implementation of Neural Networks

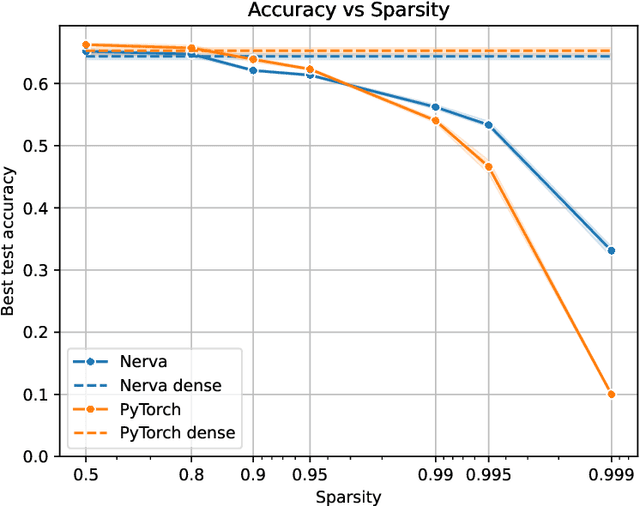
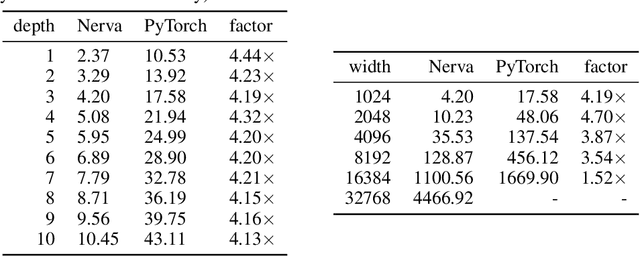
We introduce Nerva, a fast neural network library under development in C++. It supports sparsity by using the sparse matrix operations of Intel's Math Kernel Library (MKL), which eliminates the need for binary masks. We show that Nerva significantly decreases training time and memory usage while reaching equivalent accuracy to PyTorch. We run static sparse experiments with an MLP on CIFAR-10. On high sparsity levels like $99\%$, the runtime is reduced by a factor of $4\times$ compared to a PyTorch model using masks. Similar to other popular frameworks such as PyTorch and Keras, Nerva offers a Python interface for users to work with.

Scaling Continuous Latent Variable Models as Probabilistic Integral Circuits

Probabilistic integral circuits (PICs) have been recently introduced as probabilistic models enjoying the key ingredient behind expressive generative models: continuous latent variables (LVs). PICs are symbolic computational graphs defining continuous LV models as hierarchies of functions that are summed and multiplied together, or integrated over some LVs. They are tractable if LVs can be analytically integrated out, otherwise they can be approximated by tractable probabilistic circuits (PC) encoding a hierarchical numerical quadrature process, called QPCs. So far, only tree-shaped PICs have been explored, and training them via numerical quadrature requires memory-intensive processing at scale. In this paper, we address these issues, and present: (i) a pipeline for building DAG-shaped PICs out of arbitrary variable decompositions, (ii) a procedure for training PICs using tensorized circuit architectures, and (iii) neural functional sharing techniques to allow scalable training. In extensive experiments, we showcase the effectiveness of functional sharing and the superiority of QPCs over traditional PCs.

Soft Learning Probabilistic Circuits

Probabilistic Circuits (PCs) are prominent tractable probabilistic models, allowing for a range of exact inferences. This paper focuses on the main algorithm for training PCs, LearnSPN, a gold standard due to its efficiency, performance, and ease of use, in particular for tabular data. We show that LearnSPN is a greedy likelihood maximizer under mild assumptions. While inferences in PCs may use the entire circuit structure for processing queries, LearnSPN applies a hard method for learning them, propagating at each sum node a data point through one and only one of the children/edges as in a hard clustering process. We propose a new learning procedure named SoftLearn, that induces a PC using a soft clustering process. We investigate the effect of this learning-inference compatibility in PCs. Our experiments show that SoftLearn outperforms LearnSPN in many situations, yielding better likelihoods and arguably better samples. We also analyze comparable tractable models to highlight the differences between soft/hard learning and model querying.

Probabilistic Circuits with Constraints via Convex Optimization

This work addresses integrating probabilistic propositional logic constraints into the distribution encoded by a probabilistic circuit (PC). PCs are a class of tractable models that allow efficient computations (such as conditional and marginal probabilities) while achieving state-of-the-art performance in some domains. The proposed approach takes both a PC and constraints as inputs, and outputs a new PC that satisfies the constraints. This is done efficiently via convex optimization without the need to retrain the entire model. Empirical evaluations indicate that the combination of constraints and PCs can have multiple use cases, including the improvement of model performance under scarce or incomplete data, as well as the enforcement of machine learning fairness measures into the model without compromising model fitness. We believe that these ideas will open possibilities for multiple other applications involving the combination of logics and deep probabilistic models.

Probabilistic Integral Circuits

Continuous latent variables (LVs) are a key ingredient of many generative models, as they allow modelling expressive mixtures with an uncountable number of components. In contrast, probabilistic circuits (PCs) are hierarchical discrete mixtures represented as computational graphs composed of input, sum and product units. Unlike continuous LV models, PCs provide tractable inference but are limited to discrete LVs with categorical (i.e. unordered) states. We bridge these model classes by introducing probabilistic integral circuits (PICs), a new language of computational graphs that extends PCs with integral units representing continuous LVs. In the first place, PICs are symbolic computational graphs and are fully tractable in simple cases where analytical integration is possible. In practice, we parameterise PICs with light-weight neural nets delivering an intractable hierarchical continuous mixture that can be approximated arbitrarily well with large PCs using numerical quadrature. On several distribution estimation benchmarks, we show that such PIC-approximating PCs systematically outperform PCs commonly learned via expectation-maximization or SGD.

Probabilistic Multi-Dimensional Classification

Multi-dimensional classification (MDC) can be employed in a range of applications where one needs to predict multiple class variables for each given instance. Many existing MDC methods suffer from at least one of inaccuracy, scalability, limited use to certain types of data, hardness of interpretation or lack of probabilistic (uncertainty) estimations. This paper is an attempt to address all these disadvantages simultaneously. We propose a formal framework for probabilistic MDC in which learning an optimal multi-dimensional classifier can be decomposed, without loss of generality, into learning a set of (smaller) single-variable multi-class probabilistic classifiers and a directed acyclic graph. Current and future developments of both probabilistic classification and graphical model learning can directly enhance our framework, which is flexible and provably optimal. A collection of experiments is conducted to highlight the usefulness of this MDC framework.

Continuous Mixtures of Tractable Probabilistic Models

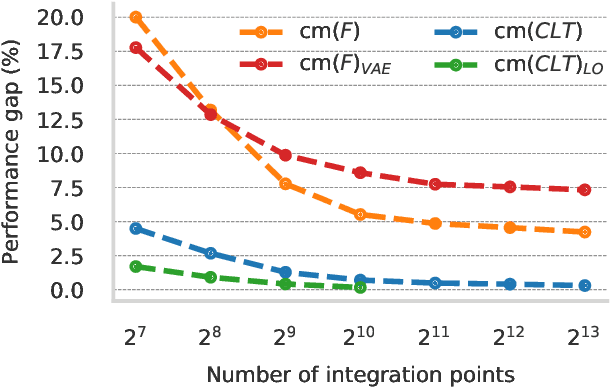
Probabilistic models based on continuous latent spaces, such as variational autoencoders, can be understood as uncountable mixture models where components depend continuously on the latent code. They have proven expressive tools for generative and probabilistic modelling, but are at odds with tractable probabilistic inference, that is, computing marginals and conditionals of the represented probability distribution. Meanwhile, tractable probabilistic models such as probabilistic circuits (PCs) can be understood as hierarchical discrete mixture models, which allows them to perform exact inference, but often they show subpar performance in comparison to continuous latent-space models. In this paper, we investigate a hybrid approach, namely continuous mixtures of tractable models with a small latent dimension. While these models are analytically intractable, they are well amenable to numerical integration schemes based on a finite set of integration points. With a large enough number of integration points the approximation becomes de-facto exact. Moreover, using a finite set of integration points, the approximation method can be compiled into a PC performing `exact inference in an approximate model'. In experiments, we show that this simple scheme proves remarkably effective, as PCs learned this way set new state-of-the-art for tractable models on many standard density estimation benchmarks.

Bayesian Kernelised Test of (In)dependence with Mixed-type Variables

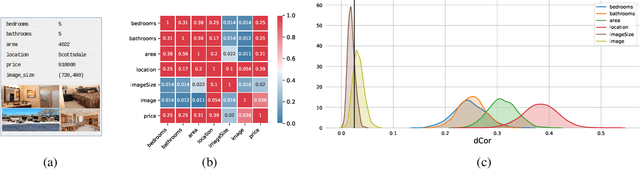
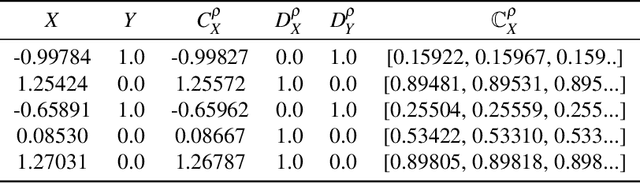
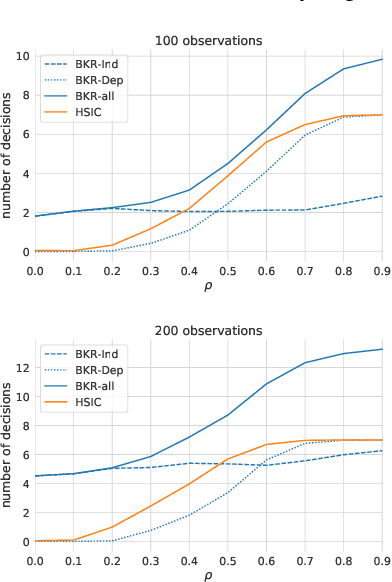
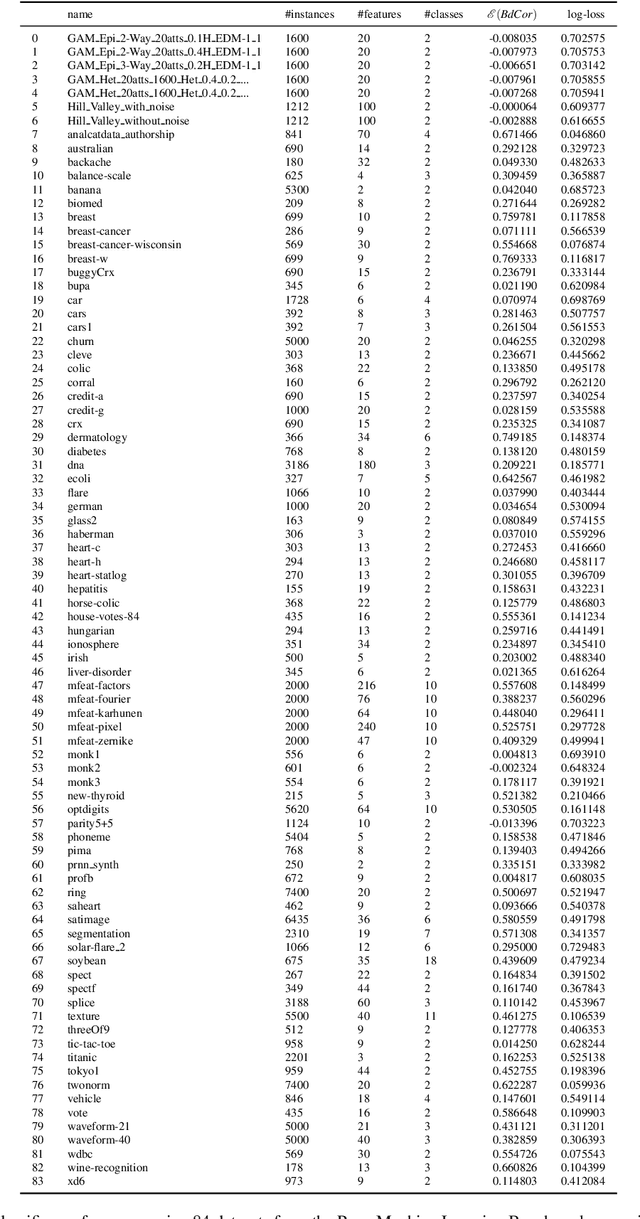
A fundamental task in AI is to assess (in)dependence between mixed-type variables (text, image, sound). We propose a Bayesian kernelised correlation test of (in)dependence using a Dirichlet process model. The new measure of (in)dependence allows us to answer some fundamental questions: Based on data, are (mixed-type) variables independent? How likely is dependence/independence to hold? How high is the probability that two mixed-type variables are more than just weakly dependent? We theoretically show the properties of the approach, as well as algorithms for fast computation with it. We empirically demonstrate the effectiveness of the proposed method by analysing its performance and by comparing it with other frequentist and Bayesian approaches on a range of datasets and tasks with mixed-type variables.

Towards Robust Classification with Deep Generative Forests

Decision Trees and Random Forests are among the most widely used machine learning models, and often achieve state-of-the-art performance in tabular, domain-agnostic datasets. Nonetheless, being primarily discriminative models they lack principled methods to manipulate the uncertainty of predictions. In this paper, we exploit Generative Forests (GeFs), a recent class of deep probabilistic models that addresses these issues by extending Random Forests to generative models representing the full joint distribution over the feature space. We demonstrate that GeFs are uncertainty-aware classifiers, capable of measuring the robustness of each prediction as well as detecting out-of-distribution samples.