Probabilistic Multi-Dimensional Classification

Multi-dimensional classification (MDC) can be employed in a range of applications where one needs to predict multiple class variables for each given instance. Many existing MDC methods suffer from at least one of inaccuracy, scalability, limited use to certain types of data, hardness of interpretation or lack of probabilistic (uncertainty) estimations. This paper is an attempt to address all these disadvantages simultaneously. We propose a formal framework for probabilistic MDC in which learning an optimal multi-dimensional classifier can be decomposed, without loss of generality, into learning a set of (smaller) single-variable multi-class probabilistic classifiers and a directed acyclic graph. Current and future developments of both probabilistic classification and graphical model learning can directly enhance our framework, which is flexible and provably optimal. A collection of experiments is conducted to highlight the usefulness of this MDC framework.

Skeptical inferences in multi-label ranking with sets of probabilities

In this paper, we consider the problem of making skeptical inferences for the multi-label ranking problem. We assume that our uncertainty is described by a convex set of probabilities (i.e. a credal set), defined over the set of labels. Instead of learning a singleton prediction (or, a completed ranking over the labels), we thus seek for skeptical inferences in terms of set-valued predictions consisting of completed rankings.

Learning Gradient Boosted Multi-label Classification Rules

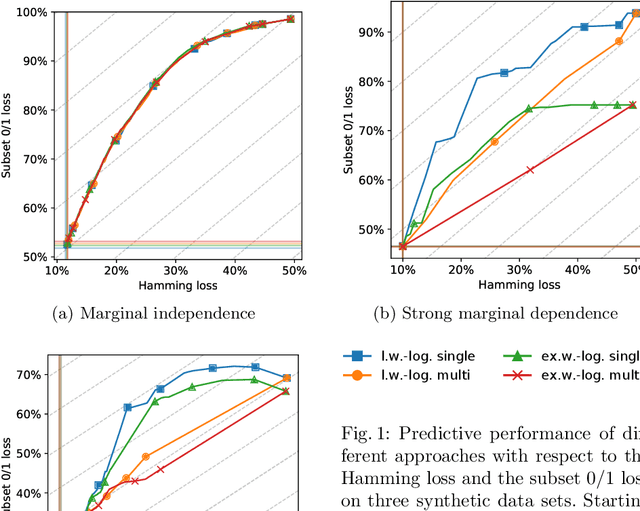
In multi-label classification, where the evaluation of predictions is less straightforward than in single-label classification, various meaningful, though different, loss functions have been proposed. Ideally, the learning algorithm should be customizable towards a specific choice of the performance measure. Modern implementations of boosting, most prominently gradient boosted decision trees, appear to be appealing from this point of view. However, they are mostly limited to single-label classification, and hence not amenable to multi-label losses unless these are label-wise decomposable. In this work, we develop a generalization of the gradient boosting framework to multi-output problems and propose an algorithm for learning multi-label classification rules that is able to minimize decomposable as well as non-decomposable loss functions. Using the well-known Hamming loss and subset 0/1 loss as representatives, we analyze the abilities and limitations of our approach on synthetic data and evaluate its predictive performance on multi-label benchmarks.

On Aggregation in Ensembles of Multilabel Classifiers

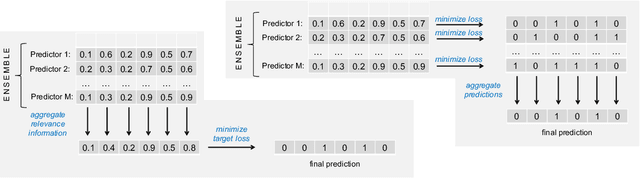
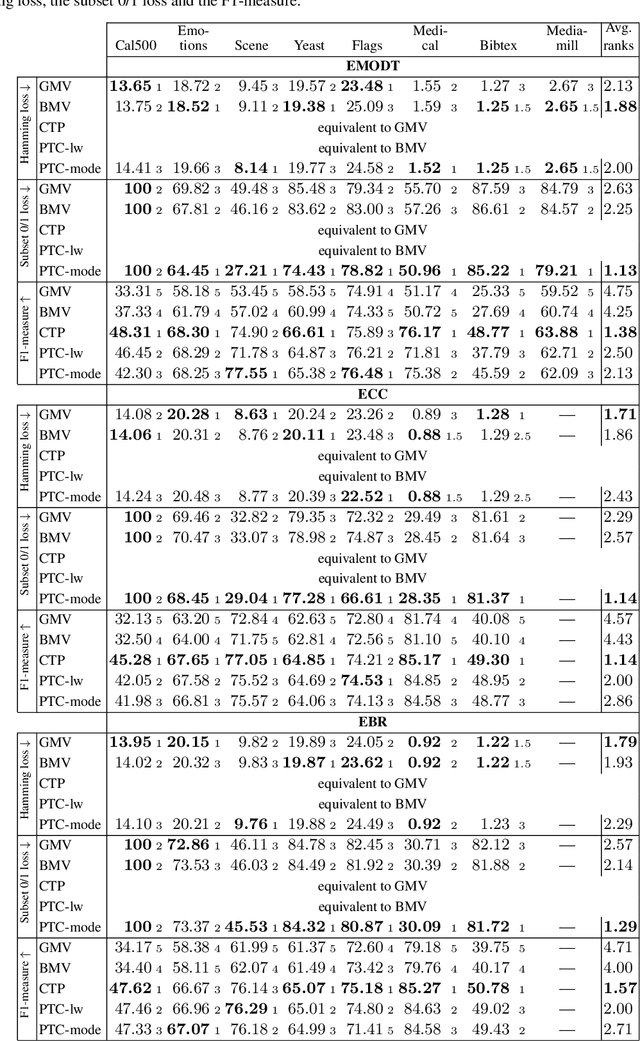
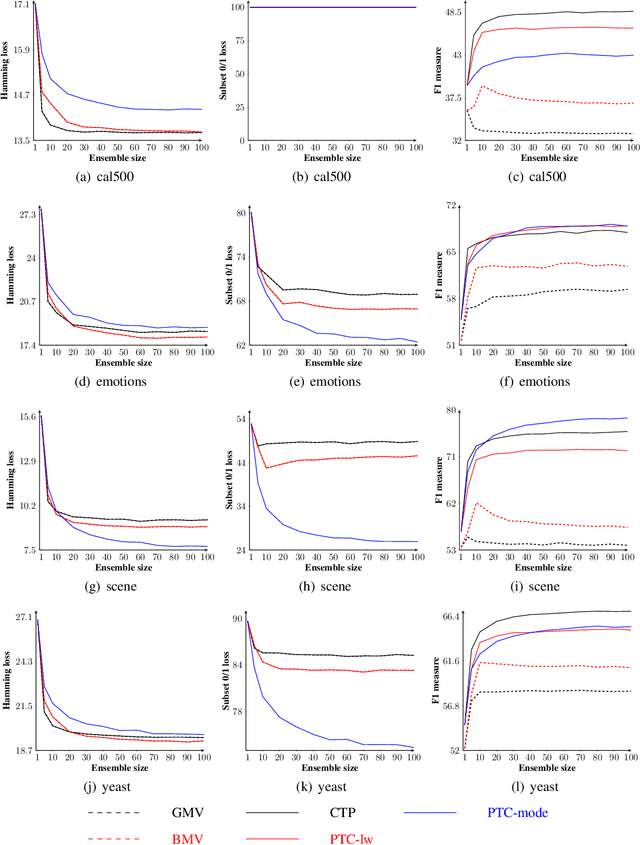
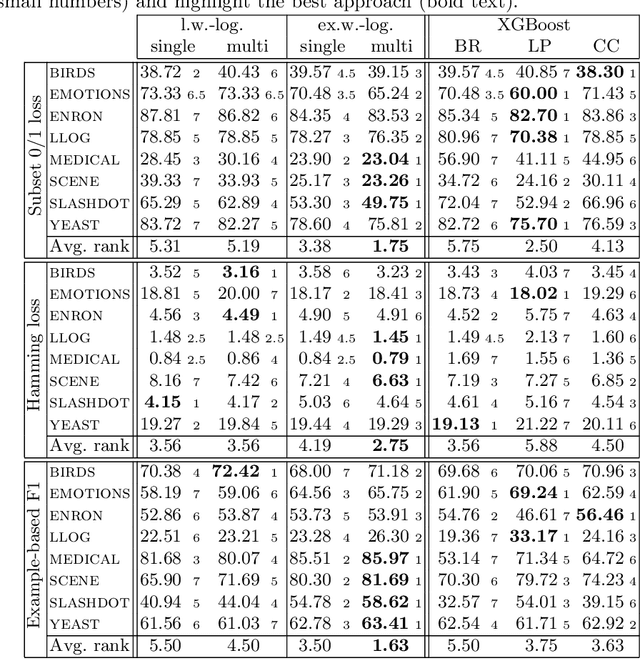
While a variety of ensemble methods for multilabel classification have been proposed in the literature, the question of how to aggregate the predictions of the individual members of the ensemble has received little attention so far. In this paper, we introduce a formal framework of ensemble multilabel classification, in which we distinguish two principal approaches: "predict then combine" (PTC), where the ensemble members first make loss minimizing predictions which are subsequently combined, and "combine then predict" (CTP), which first aggregates information such as marginal label probabilities from the individual ensemble members, and then derives a prediction from this aggregation. While both approaches generalize voting techniques commonly used for multilabel ensembles, they allow to explicitly take the target performance measure into account. Therefore, concrete instantiations of CTP and PTC can be tailored to concrete loss functions. Experimentally, we show that standard voting techniques are indeed outperformed by suitable instantiations of CTP and PTC, and provide some evidence that CTP performs well for decomposable loss functions, whereas PTC is the better choice for non-decomposable losses.

Epistemic Uncertainty Sampling

Various strategies for active learning have been proposed in the machine learning literature. In uncertainty sampling, which is among the most popular approaches, the active learner sequentially queries the label of those instances for which its current prediction is maximally uncertain. The predictions as well as the measures used to quantify the degree of uncertainty, such as entropy, are almost exclusively of a probabilistic nature. In this paper, we advocate a distinction between two different types of uncertainty, referred to as epistemic and aleatoric, in the context of active learning. Roughly speaking, these notions capture the reducible and the irreducible part of the total uncertainty in a prediction, respectively. We conjecture that, in uncertainty sampling, the usefulness of an instance is better reflected by its epistemic than by its aleatoric uncertainty. This leads us to suggest the principle of "epistemic uncertainty sampling", which we instantiate by means of a concrete approach for measuring epistemic and aleatoric uncertainty. In experimental studies, epistemic uncertainty sampling does indeed show promising performance.

Reliable Multi-label Classification: Prediction with Partial Abstention

In contrast to conventional (single-label) classification, the setting of multi-label classification (MLC) allows an instance to belong to several classes simultaneously. Thus, instead of selecting a single class label, predictions take the form of a subset of all labels. In this paper, we study an extension of the setting of MLC, in which the learner is allowed to partially abstain from a prediction, that is, to deliver predictions on some but not necessarily all class labels. We propose a formalization of MLC with abstention in terms of a generalized loss minimization problem and present first results for the case of the Hamming and rank loss, both theoretical and experimental.