Learning Gradient Boosted Multi-label Classification Rules
Paper and Code
Jun 23, 2020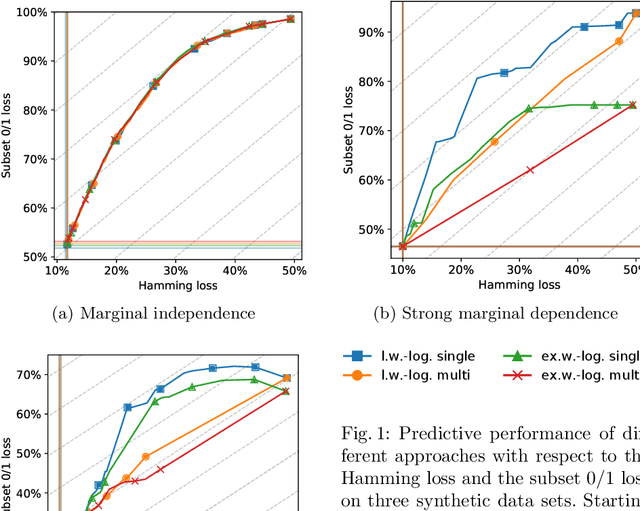
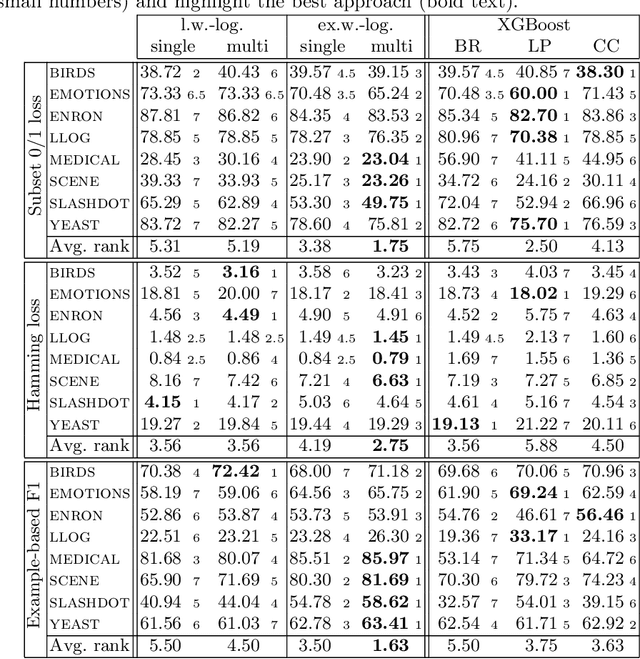
In multi-label classification, where the evaluation of predictions is less straightforward than in single-label classification, various meaningful, though different, loss functions have been proposed. Ideally, the learning algorithm should be customizable towards a specific choice of the performance measure. Modern implementations of boosting, most prominently gradient boosted decision trees, appear to be appealing from this point of view. However, they are mostly limited to single-label classification, and hence not amenable to multi-label losses unless these are label-wise decomposable. In this work, we develop a generalization of the gradient boosting framework to multi-output problems and propose an algorithm for learning multi-label classification rules that is able to minimize decomposable as well as non-decomposable loss functions. Using the well-known Hamming loss and subset 0/1 loss as representatives, we analyze the abilities and limitations of our approach on synthetic data and evaluate its predictive performance on multi-label benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge