What is the Relationship between Tensor Factorizations and Circuits (and How Can We Exploit it)?

This paper establishes a rigorous connection between circuit representations and tensor factorizations, two seemingly distinct yet fundamentally related areas. By connecting these fields, we highlight a series of opportunities that can benefit both communities. Our work generalizes popular tensor factorizations within the circuit language, and unifies various circuit learning algorithms under a single, generalized hierarchical factorization framework. Specifically, we introduce a modular "Lego block" approach to build tensorized circuit architectures. This, in turn, allows us to systematically construct and explore various circuit and tensor factorization models while maintaining tractability. This connection not only clarifies similarities and differences in existing models, but also enables the development of a comprehensive pipeline for building and optimizing new circuit/tensor factorization architectures. We show the effectiveness of our framework through extensive empirical evaluations, and highlight new research opportunities for tensor factorizations in probabilistic modeling.

Scaling Continuous Latent Variable Models as Probabilistic Integral Circuits

Probabilistic integral circuits (PICs) have been recently introduced as probabilistic models enjoying the key ingredient behind expressive generative models: continuous latent variables (LVs). PICs are symbolic computational graphs defining continuous LV models as hierarchies of functions that are summed and multiplied together, or integrated over some LVs. They are tractable if LVs can be analytically integrated out, otherwise they can be approximated by tractable probabilistic circuits (PC) encoding a hierarchical numerical quadrature process, called QPCs. So far, only tree-shaped PICs have been explored, and training them via numerical quadrature requires memory-intensive processing at scale. In this paper, we address these issues, and present: (i) a pipeline for building DAG-shaped PICs out of arbitrary variable decompositions, (ii) a procedure for training PICs using tensorized circuit architectures, and (iii) neural functional sharing techniques to allow scalable training. In extensive experiments, we showcase the effectiveness of functional sharing and the superiority of QPCs over traditional PCs.

Probabilistic Integral Circuits

Continuous latent variables (LVs) are a key ingredient of many generative models, as they allow modelling expressive mixtures with an uncountable number of components. In contrast, probabilistic circuits (PCs) are hierarchical discrete mixtures represented as computational graphs composed of input, sum and product units. Unlike continuous LV models, PCs provide tractable inference but are limited to discrete LVs with categorical (i.e. unordered) states. We bridge these model classes by introducing probabilistic integral circuits (PICs), a new language of computational graphs that extends PCs with integral units representing continuous LVs. In the first place, PICs are symbolic computational graphs and are fully tractable in simple cases where analytical integration is possible. In practice, we parameterise PICs with light-weight neural nets delivering an intractable hierarchical continuous mixture that can be approximated arbitrarily well with large PCs using numerical quadrature. On several distribution estimation benchmarks, we show that such PIC-approximating PCs systematically outperform PCs commonly learned via expectation-maximization or SGD.

Bayesian Structure Scores for Probabilistic Circuits

Probabilistic circuits (PCs) are a prominent representation of probability distributions with tractable inference. While parameter learning in PCs is rigorously studied, structure learning is often more based on heuristics than on principled objectives. In this paper, we develop Bayesian structure scores for deterministic PCs, i.e., the structure likelihood with parameters marginalized out, which are well known as rigorous objectives for structure learning in probabilistic graphical models. When used within a greedy cutset algorithm, our scores effectively protect against overfitting and yield a fast and almost hyper-parameter-free structure learner, distinguishing it from previous approaches. In experiments, we achieve good trade-offs between training time and model fit in terms of log-likelihood. Moreover, the principled nature of Bayesian scores unlocks PCs for accommodating frameworks such as structural expectation-maximization.

E(n)-equivariant Graph Neural Cellular Automata

Cellular automata (CAs) are computational models exhibiting rich dynamics emerging from the local interaction of cells arranged in a regular lattice. Graph CAs (GCAs) generalise standard CAs by allowing for arbitrary graphs rather than regular lattices, similar to how Graph Neural Networks (GNNs) generalise Convolutional NNs. Recently, Graph Neural CAs (GNCAs) have been proposed as models built on top of standard GNNs that can be trained to approximate the transition rule of any arbitrary GCA. Existing GNCAs are anisotropic in the sense that their transition rules are not equivariant to translation, rotation, and reflection of the nodes' spatial locations. However, it is desirable for instances related by such transformations to be treated identically by the model. By replacing standard graph convolutions with E(n)-equivariant ones, we avoid anisotropy by design and propose a class of isotropic automata that we call E(n)-GNCAs. These models are lightweight, but can nevertheless handle large graphs, capture complex dynamics and exhibit emergent self-organising behaviours. We showcase the broad and successful applicability of E(n)-GNCAs on three different tasks: (i) pattern formation, (ii) graph auto-encoding, and (iii) simulation of E(n)-equivariant dynamical systems.

DeeProb-kit: a Python Library for Deep Probabilistic Modelling

DeeProb-kit is a unified library written in Python consisting of a collection of deep probabilistic models (DPMs) that are tractable and exact representations for the modelled probability distributions. The availability of a representative selection of DPMs in a single library makes it possible to combine them in a straightforward manner, a common practice in deep learning research nowadays. In addition, it includes efficiently implemented learning techniques, inference routines, statistical algorithms, and provides high-quality fully-documented APIs. The development of DeeProb-kit will help the community to accelerate research on DPMs as well as to standardise their evaluation and better understand how they are related based on their expressivity.

Continuous Mixtures of Tractable Probabilistic Models

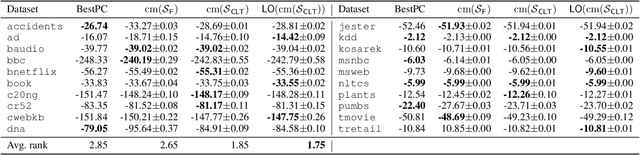
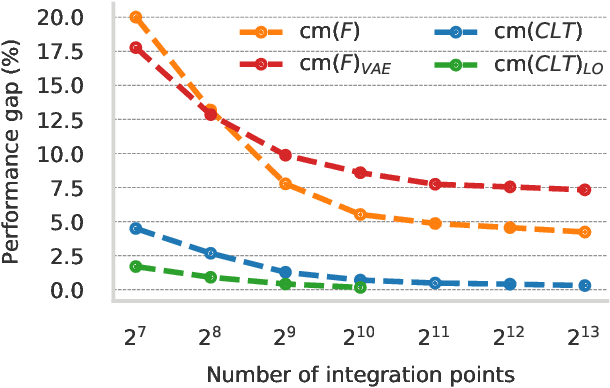
Probabilistic models based on continuous latent spaces, such as variational autoencoders, can be understood as uncountable mixture models where components depend continuously on the latent code. They have proven expressive tools for generative and probabilistic modelling, but are at odds with tractable probabilistic inference, that is, computing marginals and conditionals of the represented probability distribution. Meanwhile, tractable probabilistic models such as probabilistic circuits (PCs) can be understood as hierarchical discrete mixture models, which allows them to perform exact inference, but often they show subpar performance in comparison to continuous latent-space models. In this paper, we investigate a hybrid approach, namely continuous mixtures of tractable models with a small latent dimension. While these models are analytically intractable, they are well amenable to numerical integration schemes based on a finite set of integration points. With a large enough number of integration points the approximation becomes de-facto exact. Moreover, using a finite set of integration points, the approximation method can be compiled into a PC performing `exact inference in an approximate model'. In experiments, we show that this simple scheme proves remarkably effective, as PCs learned this way set new state-of-the-art for tractable models on many standard density estimation benchmarks.