On Faster Marginalization with Squared Circuits via Orthonormalization

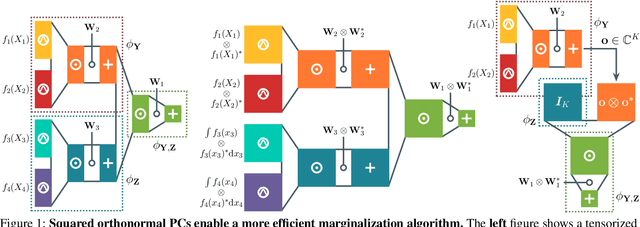
Squared tensor networks (TNs) and their generalization as parameterized computational graphs -- squared circuits -- have been recently used as expressive distribution estimators in high dimensions. However, the squaring operation introduces additional complexity when marginalizing variables or computing the partition function, which hinders their usage in machine learning applications. Canonical forms of popular TNs are parameterized via unitary matrices as to simplify the computation of particular marginals, but cannot be mapped to general circuits since these might not correspond to a known TN. Inspired by TN canonical forms, we show how to parameterize squared circuits to ensure they encode already normalized distributions. We then use this parameterization to devise an algorithm to compute any marginal of squared circuits that is more efficient than a previously known one. We conclude by formally showing the proposed parameterization comes with no expressiveness loss for many circuit classes.

Is Complex Query Answering Really Complex?

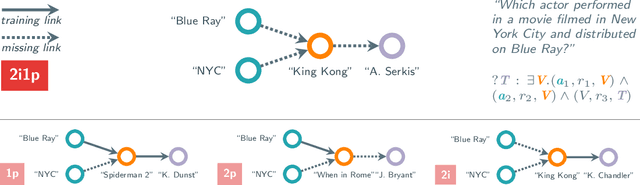
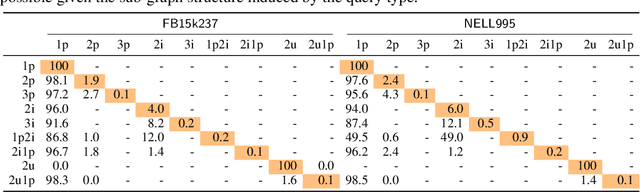
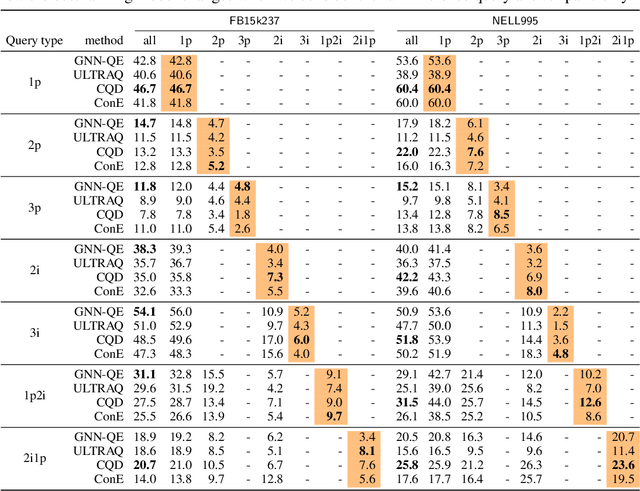
Complex query answering (CQA) on knowledge graphs (KGs) is gaining momentum as a challenging reasoning task. In this paper, we show that the current benchmarks for CQA are not really complex, and the way they are built distorts our perception of progress in this field. For example, we find that in these benchmarks, most queries (up to 98% for some query types) can be reduced to simpler problems, e.g., link prediction, where only one link needs to be predicted. The performance of state-of-the-art CQA models drops significantly when such models are evaluated on queries that cannot be reduced to easier types. Thus, we propose a set of more challenging benchmarks, composed of queries that require models to reason over multiple hops and better reflect the construction of real-world KGs. In a systematic empirical investigation, the new benchmarks show that current methods leave much to be desired from current CQA methods.

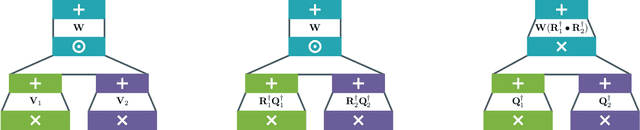
What is the Relationship between Tensor Factorizations and Circuits (and How Can We Exploit it)?

This paper establishes a rigorous connection between circuit representations and tensor factorizations, two seemingly distinct yet fundamentally related areas. By connecting these fields, we highlight a series of opportunities that can benefit both communities. Our work generalizes popular tensor factorizations within the circuit language, and unifies various circuit learning algorithms under a single, generalized hierarchical factorization framework. Specifically, we introduce a modular "Lego block" approach to build tensorized circuit architectures. This, in turn, allows us to systematically construct and explore various circuit and tensor factorization models while maintaining tractability. This connection not only clarifies similarities and differences in existing models, but also enables the development of a comprehensive pipeline for building and optimizing new circuit/tensor factorization architectures. We show the effectiveness of our framework through extensive empirical evaluations, and highlight new research opportunities for tensor factorizations in probabilistic modeling.

Sum of Squares Circuits

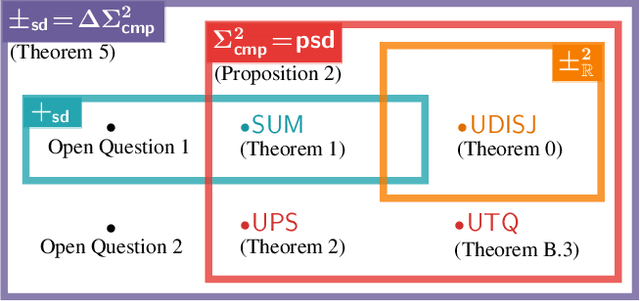
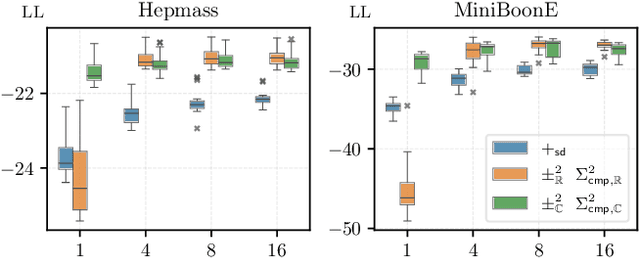
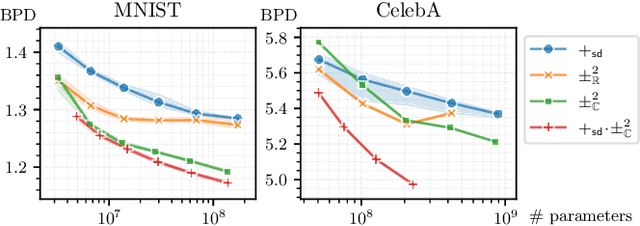
Designing expressive generative models that support exact and efficient inference is a core question in probabilistic ML. Probabilistic circuits (PCs) offer a framework where this tractability-vs-expressiveness trade-off can be analyzed theoretically. Recently, squared PCs encoding subtractive mixtures via negative parameters have emerged as tractable models that can be exponentially more expressive than monotonic PCs, i.e., PCs with positive parameters only. In this paper, we provide a more precise theoretical characterization of the expressiveness relationships among these models. First, we prove that squared PCs can be less expressive than monotonic ones. Second, we formalize a novel class of PCs -- sum of squares PCs -- that can be exponentially more expressive than both squared and monotonic PCs. Around sum of squares PCs, we build an expressiveness hierarchy that allows us to precisely unify and separate different tractable model classes such as Born Machines and PSD models, and other recently introduced tractable probabilistic models by using complex parameters. Finally, we empirically show the effectiveness of sum of squares circuits in performing distribution estimation.

What can Large Language Models Capture about Code Functional Equivalence?

Code-LLMs, LLMs pre-trained on large code corpora, have shown great progress in learning rich representations of the structure and syntax of code, successfully using it to generate or classify code fragments. At the same time, understanding if they are able to do so because they capture code semantics, and how well, is still an open question. In this paper, we tackle this problem by introducing SeqCoBench, a benchmark for systematically assessing how Code-LLMs can capture code functional equivalence. SeqCoBench contains over 20 code transformations that either preserve or alter the semantics of Python programs. We conduct extensive evaluations in different settings, including zero-shot and parameter-efficient finetuning methods on state-of-the-art (Code-)LLMs to see if they can discern semantically equivalent or different pairs of programs in SeqCoBench. We find that the performance gap between these LLMs and classical match-based retrieval scores is minimal, with both approaches showing a concerning lack of depth in understanding code semantics.

A Benchmark Suite for Systematically Evaluating Reasoning Shortcuts

The advent of powerful neural classifiers has increased interest in problems that require both learning and reasoning. These problems are critical for understanding important properties of models, such as trustworthiness, generalization, interpretability, and compliance to safety and structural constraints. However, recent research observed that tasks requiring both learning and reasoning on background knowledge often suffer from reasoning shortcuts (RSs): predictors can solve the downstream reasoning task without associating the correct concepts to the high-dimensional data. To address this issue, we introduce rsbench, a comprehensive benchmark suite designed to systematically evaluate the impact of RSs on models by providing easy access to highly customizable tasks affected by RSs. Furthermore, rsbench implements common metrics for evaluating concept quality and introduces novel formal verification procedures for assessing the presence of RSs in learning tasks. Using rsbench, we highlight that obtaining high quality concepts in both purely neural and neuro-symbolic models is a far-from-solved problem. rsbench is available at: https://unitn-sml.github.io/rsbench.

Scaling Continuous Latent Variable Models as Probabilistic Integral Circuits

Probabilistic integral circuits (PICs) have been recently introduced as probabilistic models enjoying the key ingredient behind expressive generative models: continuous latent variables (LVs). PICs are symbolic computational graphs defining continuous LV models as hierarchies of functions that are summed and multiplied together, or integrated over some LVs. They are tractable if LVs can be analytically integrated out, otherwise they can be approximated by tractable probabilistic circuits (PC) encoding a hierarchical numerical quadrature process, called QPCs. So far, only tree-shaped PICs have been explored, and training them via numerical quadrature requires memory-intensive processing at scale. In this paper, we address these issues, and present: (i) a pipeline for building DAG-shaped PICs out of arbitrary variable decompositions, (ii) a procedure for training PICs using tensorized circuit architectures, and (iii) neural functional sharing techniques to allow scalable training. In extensive experiments, we showcase the effectiveness of functional sharing and the superiority of QPCs over traditional PCs.

Towards Logically Consistent Language Models via Probabilistic Reasoning

Large language models (LLMs) are a promising venue for natural language understanding and generation tasks. However, current LLMs are far from reliable: they are prone to generate non-factual information and, more crucially, to contradict themselves when prompted to reason about beliefs of the world. These problems are currently addressed with large scale fine-tuning or by delegating consistent reasoning to external tools. In this work, we strive for a middle ground and introduce a training objective based on principled probabilistic reasoning that teaches a LLM to be consistent with external knowledge in the form of a set of facts and rules. Fine-tuning with our loss on a limited set of facts enables our LLMs to be more logically consistent than previous baselines and allows them to extrapolate to unseen but semantically similar factual knowledge more systematically.

On the Independence Assumption in Neurosymbolic Learning

State-of-the-art neurosymbolic learning systems use probabilistic reasoning to guide neural networks towards predictions that conform to logical constraints over symbols. Many such systems assume that the probabilities of the considered symbols are conditionally independent given the input to simplify learning and reasoning. We study and criticise this assumption, highlighting how it can hinder optimisation and prevent uncertainty quantification. We prove that loss functions bias conditionally independent neural networks to become overconfident in their predictions. As a result, they are unable to represent uncertainty over multiple valid options. Furthermore, we prove that these loss functions are difficult to optimise: they are non-convex, and their minima are usually highly disconnected. Our theoretical analysis gives the foundation for replacing the conditional independence assumption and designing more expressive neurosymbolic probabilistic models.

BEARS Make Neuro-Symbolic Models Aware of their Reasoning Shortcuts

Neuro-Symbolic (NeSy) predictors that conform to symbolic knowledge - encoding, e.g., safety constraints - can be affected by Reasoning Shortcuts (RSs): They learn concepts consistent with the symbolic knowledge by exploiting unintended semantics. RSs compromise reliability and generalization and, as we show in this paper, they are linked to NeSy models being overconfident about the predicted concepts. Unfortunately, the only trustworthy mitigation strategy requires collecting costly dense supervision over the concepts. Rather than attempting to avoid RSs altogether, we propose to ensure NeSy models are aware of the semantic ambiguity of the concepts they learn, thus enabling their users to identify and distrust low-quality concepts. Starting from three simple desiderata, we derive bears (BE Aware of Reasoning Shortcuts), an ensembling technique that calibrates the model's concept-level confidence without compromising prediction accuracy, thus encouraging NeSy architectures to be uncertain about concepts affected by RSs. We show empirically that bears improves RS-awareness of several state-of-the-art NeSy models, and also facilitates acquiring informative dense annotations for mitigation purposes.