Roberto Sebastiani
A Probabilistic Neuro-symbolic Layer for Algebraic Constraint Satisfaction
Mar 25, 2025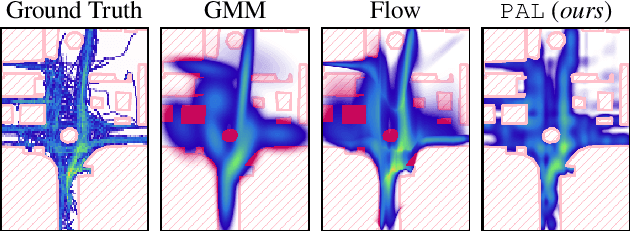
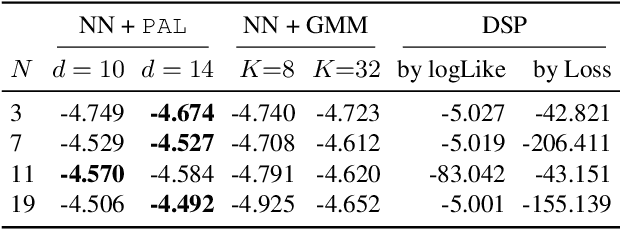
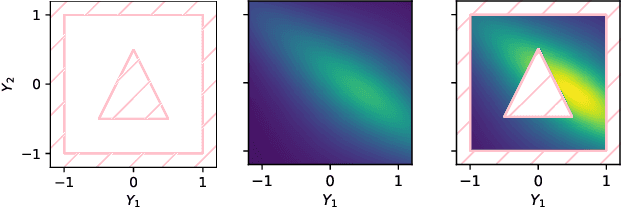
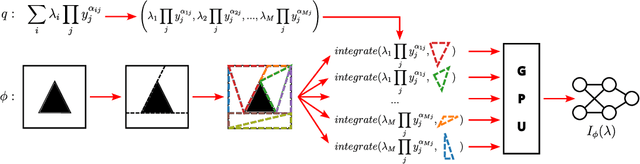
Abstract:In safety-critical applications, guaranteeing the satisfaction of constraints over continuous environments is crucial, e.g., an autonomous agent should never crash into obstacles or go off-road. Neural models struggle in the presence of these constraints, especially when they involve intricate algebraic relationships. To address this, we introduce a differentiable probabilistic layer that guarantees the satisfaction of non-convex algebraic constraints over continuous variables. This probabilistic algebraic layer (PAL) can be seamlessly plugged into any neural architecture and trained via maximum likelihood without requiring approximations. PAL defines a distribution over conjunctions and disjunctions of linear inequalities, parameterized by polynomials. This formulation enables efficient and exact renormalization via symbolic integration, which can be amortized across different data points and easily parallelized on a GPU. We showcase PAL and our integration scheme on a number of benchmarks for algebraic constraint integration and on real-world trajectory data.
Entailment vs. Verification for Partial-assignment Satisfiability and Enumeration
Mar 03, 2025Abstract:Many procedures for SAT-related problems, in particular for those requiring the complete enumeration of satisfying truth assignments, rely their efficiency and effectiveness on the detection of (possibly small) partial assignments satisfying an input formula. Surprisingly, there seems to be no unique universally-agreed definition of formula satisfaction by a partial assignment in the literature. In this paper we analyze in deep the issue of satisfaction by partial assignments, raising a flag about some ambiguities and subtleties of this concept, and investigating their practical consequences. We identify two alternative notions that are implicitly used in the literature, namely verification and entailment, which coincide if applied to CNF formulas but differ and present complementary properties if applied to non-CNF or to existentially-quantified formulas. We show that, although the former is easier to check and as such is implicitly used by most current search procedures, the latter has better theoretical properties, and can improve the efficiency and effectiveness of enumeration procedures.
Canonical Decision Diagrams Modulo Theories
Apr 25, 2024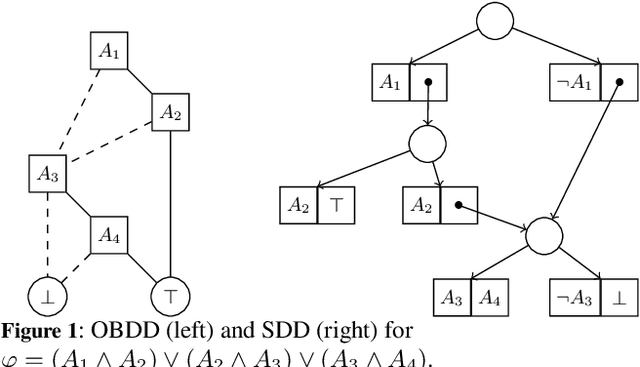
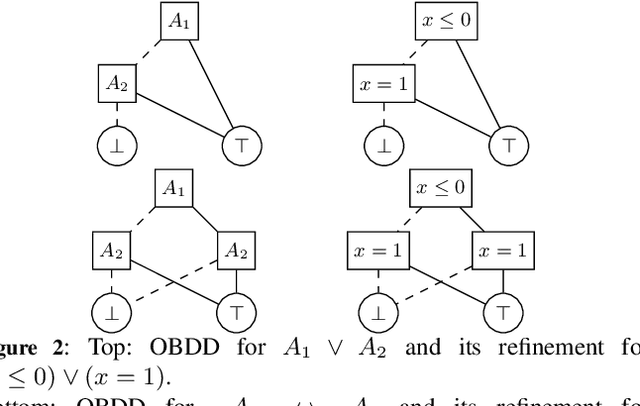
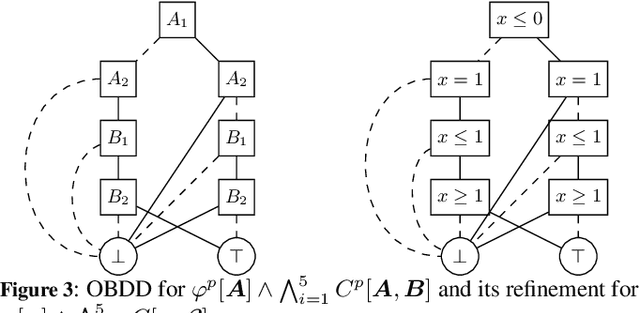
Abstract:Decision diagrams (DDs) are powerful tools to represent effectively propositional formulas, which are largely used in many domains, in particular in formal verification and in knowledge compilation. Some forms of DDs (e.g., OBDDs, SDDs) are canonical, that is, (under given conditions on the atom list) they univocally represent equivalence classes of formulas. Given the limited expressiveness of propositional logic, a few attempts to leverage DDs to SMT level have been presented in the literature. Unfortunately, these techniques still suffer from some limitations: most procedures are theory-specific; some produce theory DDs (T-DDs) which do not univocally represent T-valid formulas or T-inconsistent formulas; none of these techniques provably produces theory-canonical T-DDs, which (under given conditions on the T-atom list) univocally represent T-equivalence classes of formulas. Also, these procedures are not easy to implement, and very few implementations are actually available. In this paper, we present a novel very-general technique to leverage DDs to SMT level, which has several advantages: it is very easy to implement on top of an AllSMT solver and a DD package, which are used as blackboxes; it works for every form of DDs and every theory, or combination thereof, supported by the AllSMT solver; it produces theory-canonical T-DDs if the propositional DD is canonical. We have implemented a prototype tool for both T-OBDDs and T-SDDs on top of OBDD and SDD packages and the MathSAT SMT solver. Some preliminary empirical evaluation supports the effectiveness of the approach.
A Unified Framework for Probabilistic Verification of AI Systems via Weighted Model Integration
Feb 07, 2024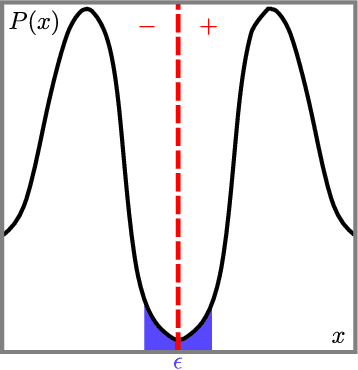

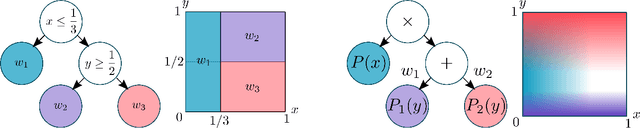
Abstract:The probabilistic formal verification (PFV) of AI systems is in its infancy. So far, approaches have been limited to ad-hoc algorithms for specific classes of models and/or properties. We propose a unifying framework for the PFV of AI systems based onWeighted Model Integration (WMI), which allows to frame the problem in very general terms. Crucially, this reduction enables the verification of many properties of interest, like fairness, robustness or monotonicity, over a wide range of machine learning models, without making strong distributional assumptions. We support the generality of the approach by solving multiple verification tasks with a single, off-the-shelf WMI solver, then discuss the scalability challenges and research directions related to this promising framework.
Enhancing SMT-based Weighted Model Integration by Structure Awareness
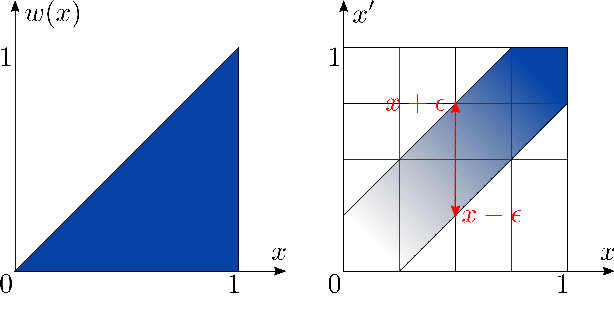
Feb 13, 2023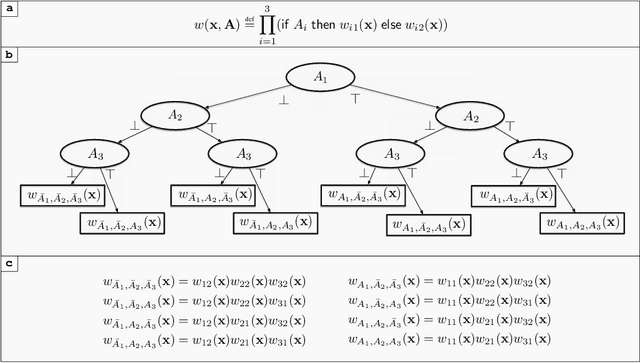

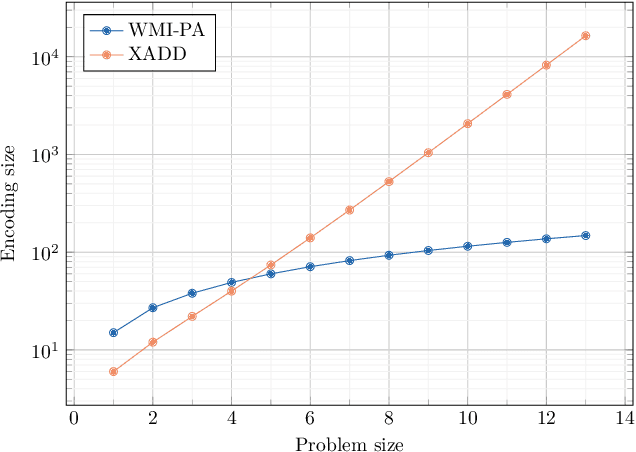
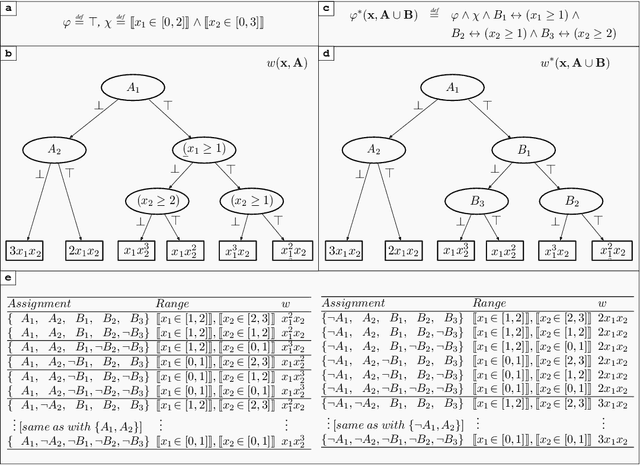
Abstract:The development of efficient exact and approximate algorithms for probabilistic inference is a long-standing goal of artificial intelligence research. Whereas substantial progress has been made in dealing with purely discrete or purely continuous domains, adapting the developed solutions to tackle hybrid domains, characterised by discrete and continuous variables and their relationships, is highly non-trivial. Weighted Model Integration (WMI) recently emerged as a unifying formalism for probabilistic inference in hybrid domains. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in drastic computational savings. Additionally, we show how SMT-based approaches can seamlessly deal with different integration techniques, both exact and approximate, significantly expanding the set of problems that can be tackled by WMI technology. An extensive experimental evaluation on both synthetic and real-world datasets confirms the substantial advantage of the proposed solution over existing alternatives. The application potential of this technology is further showcased on a prototypical task aimed at verifying the fairness of probabilistic programs.
SMT-based Weighted Model Integration with Structure Awareness
Jun 28, 2022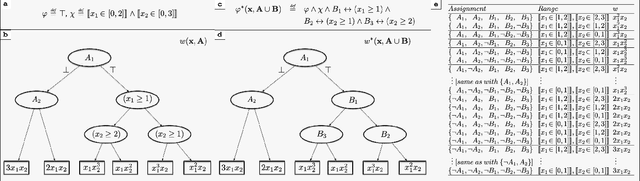
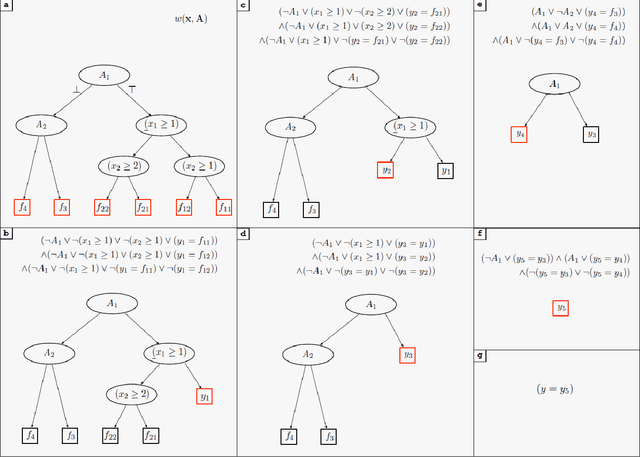


Abstract:Weighted Model Integration (WMI) is a popular formalism aimed at unifying approaches for probabilistic inference in hybrid domains, involving logical and algebraic constraints. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in substantial computational savings. An extensive experimental evaluation on both synthetic and real-world datasets confirms the advantage of the proposed solution over existing alternatives.
Are You Satisfied by This Partial Assignment?
Feb 28, 2020

Abstract:Many procedures for SAT and SAT-related problems -- in particular for those requiring the complete enumeration of satisfying truth assignments -- rely their efficiency on the detection of partial assignments satisfying an input formula. In this paper we analyze the notion of partial-assignment satisfiability -- in particular when dealing with non-CNF and existentially-quantified formulas -- raising a flag about the ambiguities and subtleties of this concept, and investigating their practical consequences. This may drive the development of more effective assignment-enumeration algorithms.
Multi-Object Reasoning with Constrained Goal Models
Nov 25, 2016



Abstract:Goal models have been widely used in Computer Science to represent software requirements, business objectives, and design qualities. Existing goal modelling techniques, however, have shown limitations of expressiveness and/or tractability in coping with complex real-world problems. In this work, we exploit advances in automated reasoning technologies, notably Satisfiability and Optimization Modulo Theories (SMT/OMT), and we propose and formalize: (i) an extended modelling language for goals, namely the Constrained Goal Model (CGM), which makes explicit the notion of goal refinement and of domain assumption, allows for expressing preferences between goals and refinements, and allows for associating numerical attributes to goals and refinements for defining constraints and optimization goals over multiple objective functions, refinements and their numerical attributes; (ii) a novel set of automated reasoning functionalities over CGMs, allowing for automatically generating suitable refinements of input CGMs, under user-specified assumptions and constraints, that also maximize preferences and optimize given objective functions. We have implemented these modelling and reasoning functionalities in a tool, named CGM-Tool, using the OMT solver OptiMathSAT as automated reasoning backend. Moreover, we have conducted an experimental evaluation on large CGMs to support the claim that our proposal scales well for goal models with thousands of elements.
Structured Learning Modulo Theories
Dec 18, 2014



Abstract:Modelling problems containing a mixture of Boolean and numerical variables is a long-standing interest of Artificial Intelligence. However, performing inference and learning in hybrid domains is a particularly daunting task. The ability to model this kind of domains is crucial in "learning to design" tasks, that is, learning applications where the goal is to learn from examples how to perform automatic {\em de novo} design of novel objects. In this paper we present Structured Learning Modulo Theories, a max-margin approach for learning in hybrid domains based on Satisfiability Modulo Theories, which allows to combine Boolean reasoning and optimization over continuous linear arithmetical constraints. The main idea is to leverage a state-of-the-art generalized Satisfiability Modulo Theory solver for implementing the inference and separation oracles of Structured Output SVMs. We validate our method on artificial and real world scenarios.
Hybrid SRL with Optimization Modulo Theories
Feb 18, 2014Abstract:Generally speaking, the goal of constructive learning could be seen as, given an example set of structured objects, to generate novel objects with similar properties. From a statistical-relational learning (SRL) viewpoint, the task can be interpreted as a constraint satisfaction problem, i.e. the generated objects must obey a set of soft constraints, whose weights are estimated from the data. Traditional SRL approaches rely on (finite) First-Order Logic (FOL) as a description language, and on MAX-SAT solvers to perform inference. Alas, FOL is unsuited for con- structive problems where the objects contain a mixture of Boolean and numerical variables. It is in fact difficult to implement, e.g. linear arithmetic constraints within the language of FOL. In this paper we propose a novel class of hybrid SRL methods that rely on Satisfiability Modulo Theories, an alternative class of for- mal languages that allow to describe, and reason over, mixed Boolean-numerical objects and constraints. The resulting methods, which we call Learning Mod- ulo Theories, are formulated within the structured output SVM framework, and employ a weighted SMT solver as an optimization oracle to perform efficient in- ference and discriminative max margin weight learning. We also present a few examples of constructive learning applications enabled by our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge