Canonical Decision Diagrams Modulo Theories

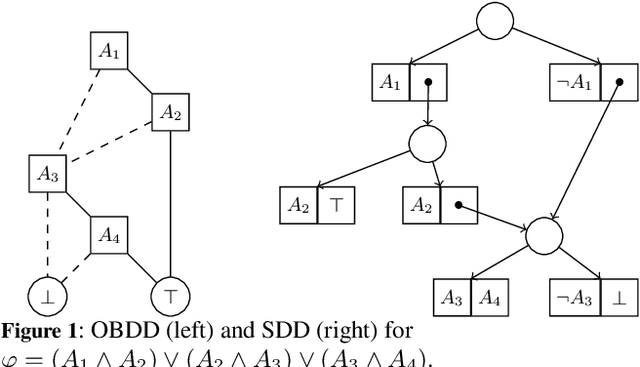
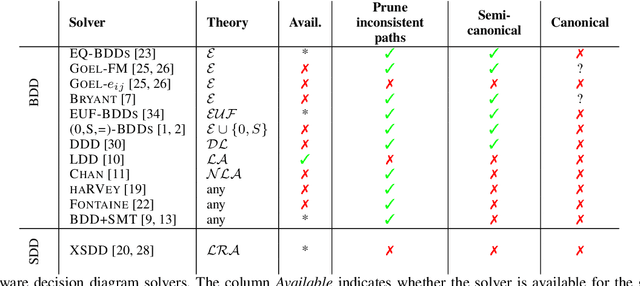
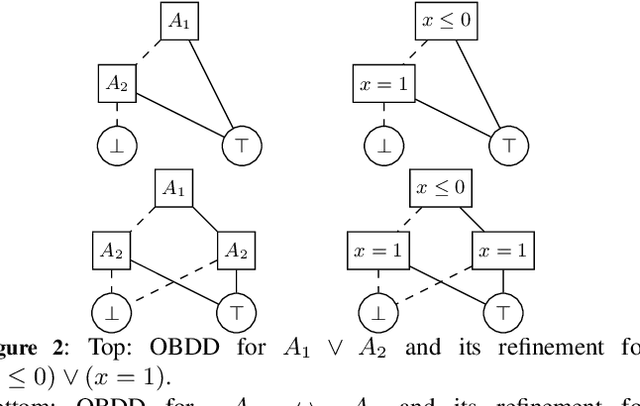
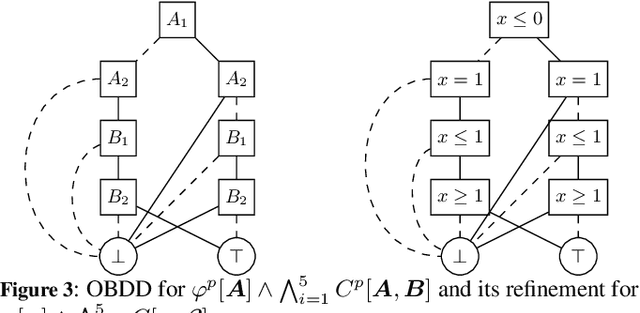
Decision diagrams (DDs) are powerful tools to represent effectively propositional formulas, which are largely used in many domains, in particular in formal verification and in knowledge compilation. Some forms of DDs (e.g., OBDDs, SDDs) are canonical, that is, (under given conditions on the atom list) they univocally represent equivalence classes of formulas. Given the limited expressiveness of propositional logic, a few attempts to leverage DDs to SMT level have been presented in the literature. Unfortunately, these techniques still suffer from some limitations: most procedures are theory-specific; some produce theory DDs (T-DDs) which do not univocally represent T-valid formulas or T-inconsistent formulas; none of these techniques provably produces theory-canonical T-DDs, which (under given conditions on the T-atom list) univocally represent T-equivalence classes of formulas. Also, these procedures are not easy to implement, and very few implementations are actually available. In this paper, we present a novel very-general technique to leverage DDs to SMT level, which has several advantages: it is very easy to implement on top of an AllSMT solver and a DD package, which are used as blackboxes; it works for every form of DDs and every theory, or combination thereof, supported by the AllSMT solver; it produces theory-canonical T-DDs if the propositional DD is canonical. We have implemented a prototype tool for both T-OBDDs and T-SDDs on top of OBDD and SDD packages and the MathSAT SMT solver. Some preliminary empirical evaluation supports the effectiveness of the approach.

Enhancing SMT-based Weighted Model Integration by Structure Awareness

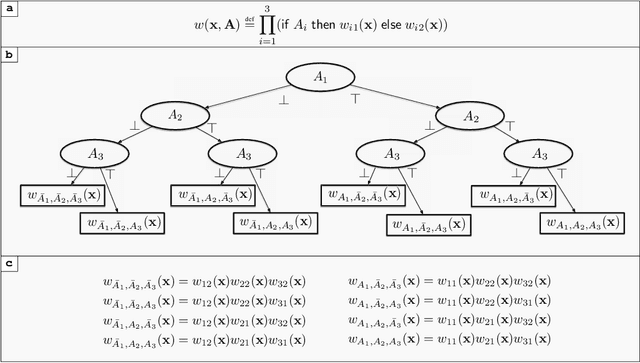
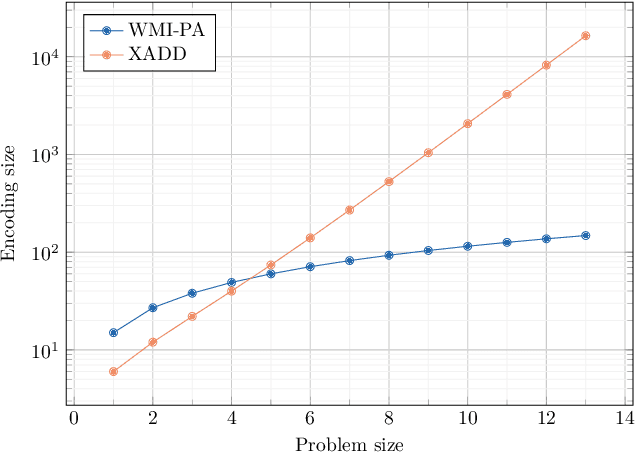
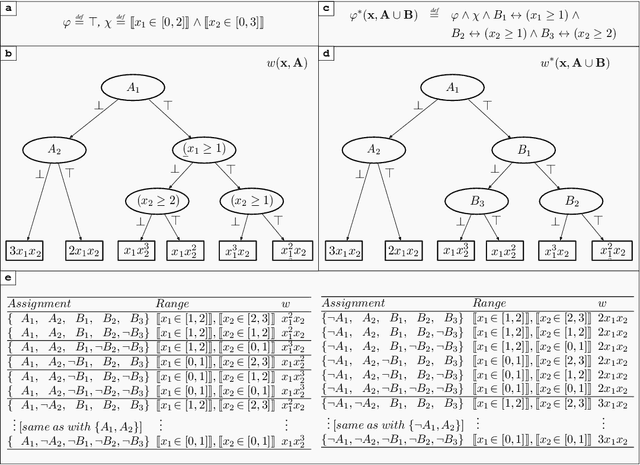
The development of efficient exact and approximate algorithms for probabilistic inference is a long-standing goal of artificial intelligence research. Whereas substantial progress has been made in dealing with purely discrete or purely continuous domains, adapting the developed solutions to tackle hybrid domains, characterised by discrete and continuous variables and their relationships, is highly non-trivial. Weighted Model Integration (WMI) recently emerged as a unifying formalism for probabilistic inference in hybrid domains. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in drastic computational savings. Additionally, we show how SMT-based approaches can seamlessly deal with different integration techniques, both exact and approximate, significantly expanding the set of problems that can be tackled by WMI technology. An extensive experimental evaluation on both synthetic and real-world datasets confirms the substantial advantage of the proposed solution over existing alternatives. The application potential of this technology is further showcased on a prototypical task aimed at verifying the fairness of probabilistic programs.

SMT-based Weighted Model Integration with Structure Awareness

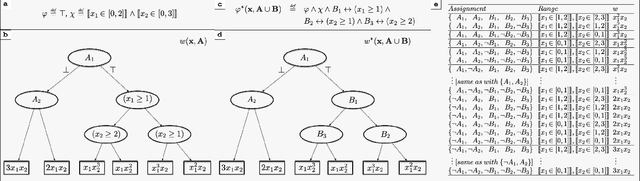
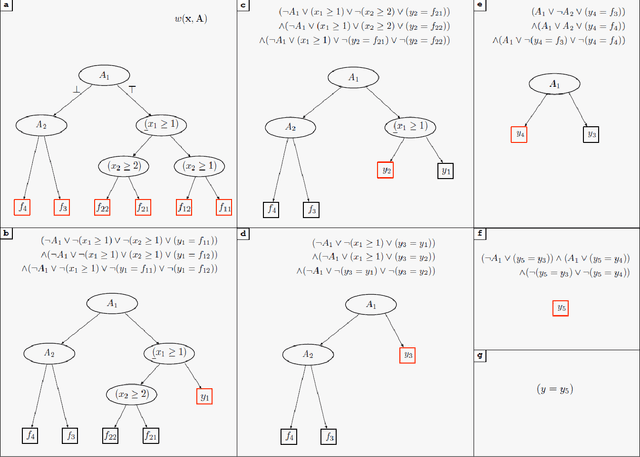
Weighted Model Integration (WMI) is a popular formalism aimed at unifying approaches for probabilistic inference in hybrid domains, involving logical and algebraic constraints. Despite a considerable amount of recent work, allowing WMI algorithms to scale with the complexity of the hybrid problem is still a challenge. In this paper we highlight some substantial limitations of existing state-of-the-art solutions, and develop an algorithm that combines SMT-based enumeration, an efficient technique in formal verification, with an effective encoding of the problem structure. This allows our algorithm to avoid generating redundant models, resulting in substantial computational savings. An extensive experimental evaluation on both synthetic and real-world datasets confirms the advantage of the proposed solution over existing alternatives.