On Faster Marginalization with Squared Circuits via Orthonormalization

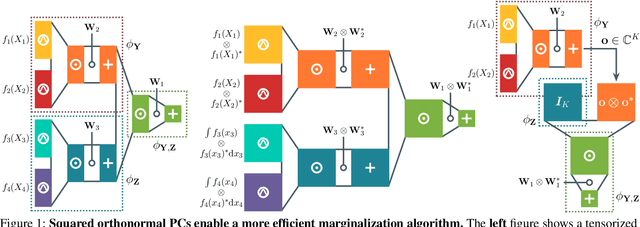
Squared tensor networks (TNs) and their generalization as parameterized computational graphs -- squared circuits -- have been recently used as expressive distribution estimators in high dimensions. However, the squaring operation introduces additional complexity when marginalizing variables or computing the partition function, which hinders their usage in machine learning applications. Canonical forms of popular TNs are parameterized via unitary matrices as to simplify the computation of particular marginals, but cannot be mapped to general circuits since these might not correspond to a known TN. Inspired by TN canonical forms, we show how to parameterize squared circuits to ensure they encode already normalized distributions. We then use this parameterization to devise an algorithm to compute any marginal of squared circuits that is more efficient than a previously known one. We conclude by formally showing the proposed parameterization comes with no expressiveness loss for many circuit classes.

Is Complex Query Answering Really Complex?

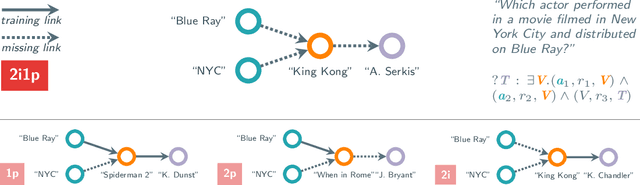
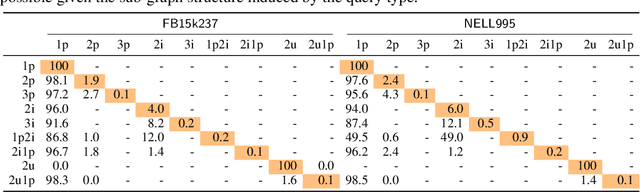
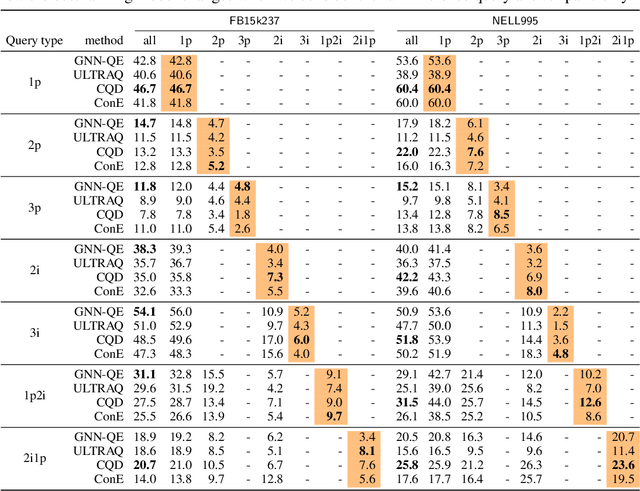
Complex query answering (CQA) on knowledge graphs (KGs) is gaining momentum as a challenging reasoning task. In this paper, we show that the current benchmarks for CQA are not really complex, and the way they are built distorts our perception of progress in this field. For example, we find that in these benchmarks, most queries (up to 98% for some query types) can be reduced to simpler problems, e.g., link prediction, where only one link needs to be predicted. The performance of state-of-the-art CQA models drops significantly when such models are evaluated on queries that cannot be reduced to easier types. Thus, we propose a set of more challenging benchmarks, composed of queries that require models to reason over multiple hops and better reflect the construction of real-world KGs. In a systematic empirical investigation, the new benchmarks show that current methods leave much to be desired from current CQA methods.

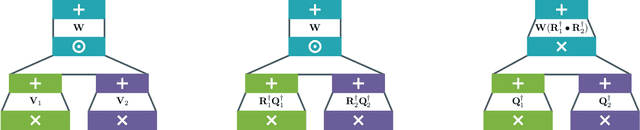
What is the Relationship between Tensor Factorizations and Circuits (and How Can We Exploit it)?

This paper establishes a rigorous connection between circuit representations and tensor factorizations, two seemingly distinct yet fundamentally related areas. By connecting these fields, we highlight a series of opportunities that can benefit both communities. Our work generalizes popular tensor factorizations within the circuit language, and unifies various circuit learning algorithms under a single, generalized hierarchical factorization framework. Specifically, we introduce a modular "Lego block" approach to build tensorized circuit architectures. This, in turn, allows us to systematically construct and explore various circuit and tensor factorization models while maintaining tractability. This connection not only clarifies similarities and differences in existing models, but also enables the development of a comprehensive pipeline for building and optimizing new circuit/tensor factorization architectures. We show the effectiveness of our framework through extensive empirical evaluations, and highlight new research opportunities for tensor factorizations in probabilistic modeling.

Sum of Squares Circuits

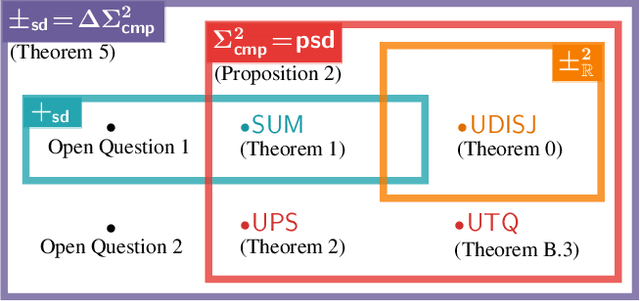
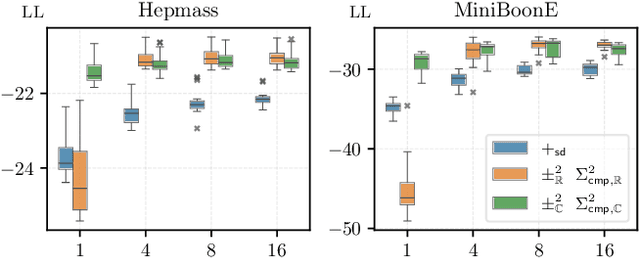
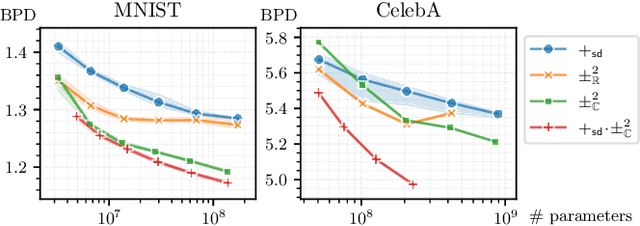
Designing expressive generative models that support exact and efficient inference is a core question in probabilistic ML. Probabilistic circuits (PCs) offer a framework where this tractability-vs-expressiveness trade-off can be analyzed theoretically. Recently, squared PCs encoding subtractive mixtures via negative parameters have emerged as tractable models that can be exponentially more expressive than monotonic PCs, i.e., PCs with positive parameters only. In this paper, we provide a more precise theoretical characterization of the expressiveness relationships among these models. First, we prove that squared PCs can be less expressive than monotonic ones. Second, we formalize a novel class of PCs -- sum of squares PCs -- that can be exponentially more expressive than both squared and monotonic PCs. Around sum of squares PCs, we build an expressiveness hierarchy that allows us to precisely unify and separate different tractable model classes such as Born Machines and PSD models, and other recently introduced tractable probabilistic models by using complex parameters. Finally, we empirically show the effectiveness of sum of squares circuits in performing distribution estimation.

Subtractive Mixture Models via Squaring: Representation and Learning

Mixture models are traditionally represented and learned by adding several distributions as components. Allowing mixtures to subtract probability mass or density can drastically reduce the number of components needed to model complex distributions. However, learning such subtractive mixtures while ensuring they still encode a non-negative function is challenging. We investigate how to learn and perform inference on deep subtractive mixtures by squaring them. We do this in the framework of probabilistic circuits, which enable us to represent tensorized mixtures and generalize several other subtractive models. We theoretically prove that the class of squared circuits allowing subtractions can be exponentially more expressive than traditional additive mixtures; and, we empirically show this increased expressiveness on a series of real-world distribution estimation tasks.

How to Turn Your Knowledge Graph Embeddings into Generative Models via Probabilistic Circuits

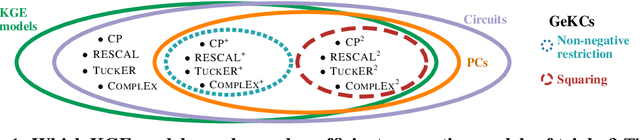
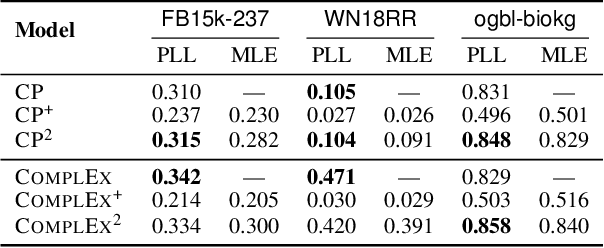
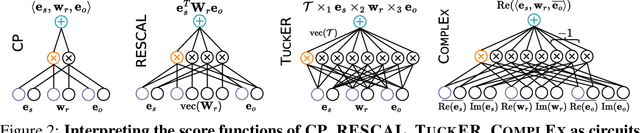
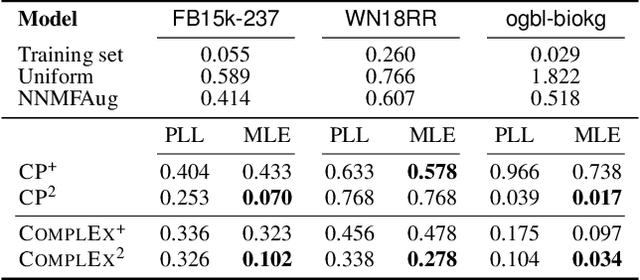
Some of the most successful knowledge graph embedding (KGE) models for link prediction -- CP, RESCAL, TuckER, ComplEx -- can be interpreted as energy-based models. Under this perspective they are not amenable for exact maximum-likelihood estimation (MLE), sampling and struggle to integrate logical constraints. This work re-interprets the score functions of these KGEs as circuits -- constrained computational graphs allowing efficient marginalisation. Then, we design two recipes to obtain efficient generative circuit models by either restricting their activations to be non-negative or squaring their outputs. Our interpretation comes with little or no loss of performance for link prediction, while the circuits framework unlocks exact learning by MLE, efficient sampling of new triples, and guarantee that logical constraints are satisfied by design. Furthermore, our models scale more gracefully than the original KGEs on graphs with millions of entities.

DeeProb-kit: a Python Library for Deep Probabilistic Modelling

DeeProb-kit is a unified library written in Python consisting of a collection of deep probabilistic models (DPMs) that are tractable and exact representations for the modelled probability distributions. The availability of a representative selection of DPMs in a single library makes it possible to combine them in a straightforward manner, a common practice in deep learning research nowadays. In addition, it includes efficiently implemented learning techniques, inference routines, statistical algorithms, and provides high-quality fully-documented APIs. The development of DeeProb-kit will help the community to accelerate research on DPMs as well as to standardise their evaluation and better understand how they are related based on their expressivity.