On the Robustness of the Successive Projection Algorithm

The successive projection algorithm (SPA) is a workhorse algorithm to learn the $r$ vertices of the convex hull of a set of $(r-1)$-dimensional data points, a.k.a. a latent simplex, which has numerous applications in data science. In this paper, we revisit the robustness to noise of SPA and several of its variants. In particular, when $r \geq 3$, we prove the tightness of the existing error bounds for SPA and for two more robust preconditioned variants of SPA. We also provide significantly improved error bounds for SPA, by a factor proportional to the conditioning of the $r$ vertices, in two special cases: for the first extracted vertex, and when $r \leq 2$. We then provide further improvements for the error bounds of a translated version of SPA proposed by Arora et al. (''A practical algorithm for topic modeling with provable guarantees'', ICML, 2013) in two special cases: for the first two extracted vertices, and when $r \leq 3$. Finally, we propose a new more robust variant of SPA that first shifts and lifts the data points in order to minimize the conditioning of the problem. We illustrate our results on synthetic data.

Orthogonal Nonnegative Matrix Factorization with the Kullback-Leibler divergence

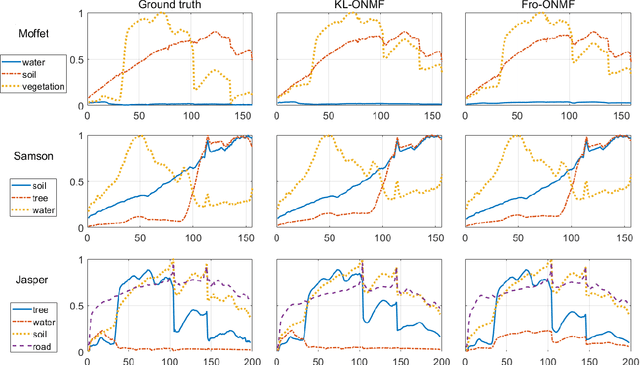
Orthogonal nonnegative matrix factorization (ONMF) has become a standard approach for clustering. As far as we know, most works on ONMF rely on the Frobenius norm to assess the quality of the approximation. This paper presents a new model and algorithm for ONMF that minimizes the Kullback-Leibler (KL) divergence. As opposed to the Frobenius norm which assumes Gaussian noise, the KL divergence is the maximum likelihood estimator for Poisson-distributed data, which can model better vectors of word counts in document data sets and photo counting processes in imaging. We have developed an algorithm based on alternating optimization, KL-ONMF, and show that it performs favorably with the Frobenius-norm based ONMF for document classification and hyperspectral image unmixing.

Dual Simplex Volume Maximization for Simplex-Structured Matrix Factorization

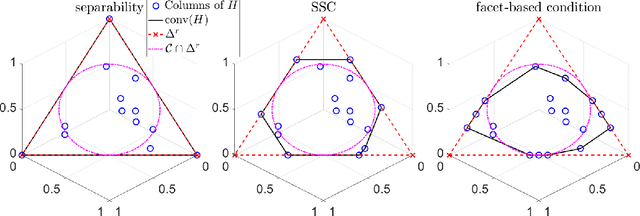
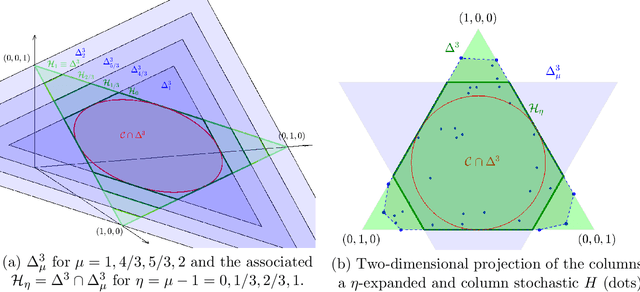
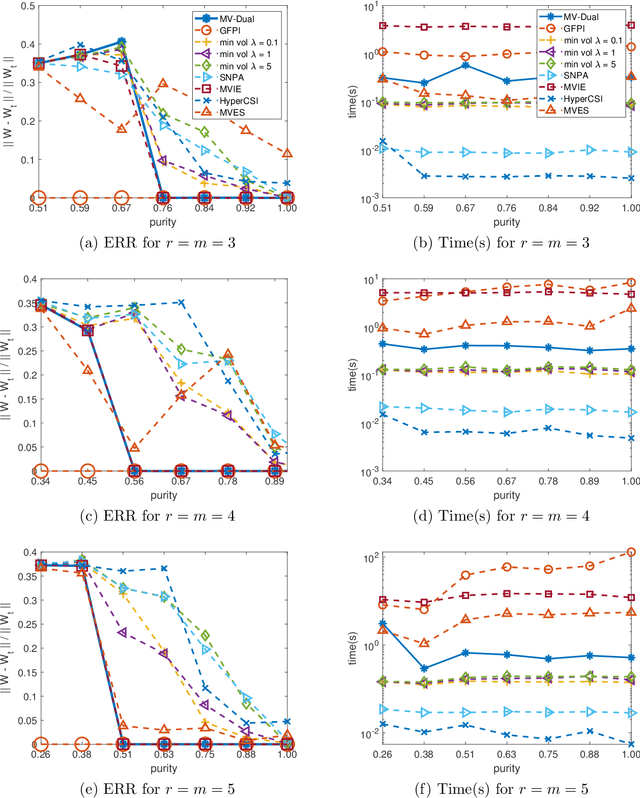
Simplex-structured matrix factorization (SSMF) is a generalization of nonnegative matrix factorization, a fundamental interpretable data analysis model, and has applications in hyperspectral unmixing and topic modeling. To obtain identifiable solutions, a standard approach is to find minimum-volume solutions. By taking advantage of the duality/polarity concept for polytopes, we convert minimum-volume SSMF in the primal space to a maximum-volume problem in the dual space. We first prove the identifiability of this maximum-volume dual problem. Then, we use this dual formulation to provide a novel optimization approach which bridges the gap between two existing families of algorithms for SSMF, namely volume minimization and facet identification. Numerical experiments show that the proposed approach performs favorably compared to the state-of-the-art SSMF algorithms.

Checking the Sufficiently Scattered Condition using a Global Non-Convex Optimization Software

The sufficiently scattered condition (SSC) is a key condition in the study of identifiability of various matrix factorization problems, including nonnegative, minimum-volume, symmetric, simplex-structured, and polytopic matrix factorizations. The SSC allows one to guarantee that the computed matrix factorization is unique/identifiable, up to trivial ambiguities. However, this condition is NP-hard to check in general. In this paper, we show that it can however be checked in a reasonable amount of time in realistic scenarios, when the factorization rank is not too large. This is achieved by formulating the problem as a non-convex quadratic optimization problem over a bounded set. We use the global non-convex optimization software Gurobi, and showcase the usefulness of this code on synthetic data sets and on real-world hyperspectral images.

Block Majorization Minimization with Extrapolation and Application to $β$-NMF

We propose a Block Majorization Minimization method with Extrapolation (BMMe) for solving a class of multi-convex optimization problems. The extrapolation parameters of BMMe are updated using a novel adaptive update rule. By showing that block majorization minimization can be reformulated as a block mirror descent method, with the Bregman divergence adaptively updated at each iteration, we establish subsequential convergence for BMMe. We use this method to design efficient algorithms to tackle nonnegative matrix factorization problems with the $\beta$-divergences ($\beta$-NMF) for $\beta\in [1,2]$. These algorithms, which are multiplicative updates with extrapolation, benefit from our novel results that offer convergence guarantees. We also empirically illustrate the significant acceleration of BMMe for $\beta$-NMF through extensive experiments.

Subtractive Mixture Models via Squaring: Representation and Learning

Mixture models are traditionally represented and learned by adding several distributions as components. Allowing mixtures to subtract probability mass or density can drastically reduce the number of components needed to model complex distributions. However, learning such subtractive mixtures while ensuring they still encode a non-negative function is challenging. We investigate how to learn and perform inference on deep subtractive mixtures by squaring them. We do this in the framework of probabilistic circuits, which enable us to represent tensorized mixtures and generalize several other subtractive models. We theoretically prove that the class of squared circuits allowing subtractions can be exponentially more expressive than traditional additive mixtures; and, we empirically show this increased expressiveness on a series of real-world distribution estimation tasks.

Deep Nonnegative Matrix Factorization with Beta Divergences

Deep Nonnegative Matrix Factorization (deep NMF) has recently emerged as a valuable technique for extracting multiple layers of features across different scales. However, all existing deep NMF models and algorithms have primarily centered their evaluation on the least squares error, which may not be the most appropriate metric for assessing the quality of approximations on diverse datasets. For instance, when dealing with data types such as audio signals and documents, it is widely acknowledged that $\beta$-divergences offer a more suitable alternative. In this paper, we develop new models and algorithms for deep NMF using $\beta$-divergences. Subsequently, we apply these techniques to the extraction of facial features, the identification of topics within document collections, and the identification of materials within hyperspectral images.

Algorithms for Boolean Matrix Factorization using Integer Programming

Boolean matrix factorization (BMF) approximates a given binary input matrix as the product of two smaller binary factors. As opposed to binary matrix factorization which uses standard arithmetic, BMF uses the Boolean OR and Boolean AND operations to perform matrix products, which leads to lower reconstruction errors. BMF is an NP-hard problem. In this paper, we first propose an alternating optimization (AO) strategy that solves the subproblem in one factor matrix in BMF using an integer program (IP). We also provide two ways to initialize the factors within AO. Then, we show how several solutions of BMF can be combined optimally using another IP. This allows us to come up with a new algorithm: it generates several solutions using AO and then combines them in an optimal way. Experiments show that our algorithms (available on gitlab) outperform the state of the art on medium-scale problems.

Accelerated Algorithms for Nonlinear Matrix Decomposition with the ReLU function

In this paper, we study the following nonlinear matrix decomposition (NMD) problem: given a sparse nonnegative matrix $X$, find a low-rank matrix $\Theta$ such that $X \approx f(\Theta)$, where $f$ is an element-wise nonlinear function. We focus on the case where $f(\cdot) = \max(0, \cdot)$, the rectified unit (ReLU) non-linear activation. We refer to the corresponding problem as ReLU-NMD. We first provide a brief overview of the existing approaches that were developed to tackle ReLU-NMD. Then we introduce two new algorithms: (1) aggressive accelerated NMD (A-NMD) which uses an adaptive Nesterov extrapolation to accelerate an existing algorithm, and (2) three-block NMD (3B-NMD) which parametrizes $\Theta = WH$ and leads to a significant reduction in the computational cost. We also propose an effective initialization strategy based on the nuclear norm as a proxy for the rank function. We illustrate the effectiveness of the proposed algorithms (available on gitlab) on synthetic and real-world data sets.

Bounded Simplex-Structured Matrix Factorization

In this paper, we propose a new low-rank matrix factorization model dubbed bounded simplex-structured matrix factorization (BSSMF). Given an input matrix $X$ and a factorization rank $r$, BSSMF looks for a matrix $W$ with $r$ columns and a matrix $H$ with $r$ rows such that $X \approx WH$ where the entries in each column of $W$ are bounded, that is, they belong to given intervals, and the columns of $H$ belong to the probability simplex, that is, $H$ is column stochastic. BSSMF generalizes nonnegative matrix factorization (NMF), and simplex-structured matrix factorization (SSMF). BSSMF is particularly well suited when the entries of the input matrix $X$ belong to a given interval; for example when the rows of $X$ represent images, or $X$ is a rating matrix such as in the Netflix and MovieLens data sets where the entries of $X$ belong to the interval $[1,5]$. The simplex-structured matrix $H$ not only leads to an easily understandable decomposition providing a soft clustering of the columns of $X$, but implies that the entries of each column of $WH$ belong to the same intervals as the columns of $W$. In this paper, we first propose a fast algorithm for BSSMF, even in the presence of missing data in $X$. Then we provide identifiability conditions for BSSMF, that is, we provide conditions under which BSSMF admits a unique decomposition, up to trivial ambiguities. Finally, we illustrate the effectiveness of BSSMF on two applications: extraction of features in a set of images, and the matrix completion problem for recommender systems.