Dual Simplex Volume Maximization for Simplex-Structured Matrix Factorization
Paper and Code
Mar 29, 2024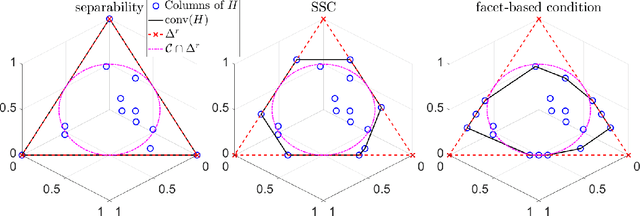
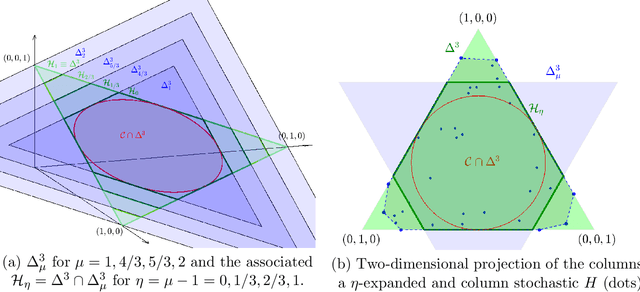
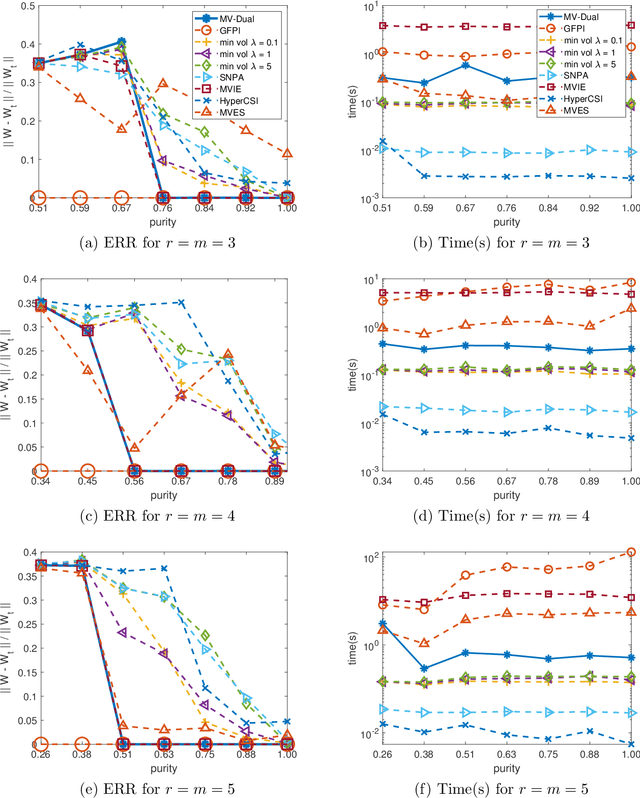
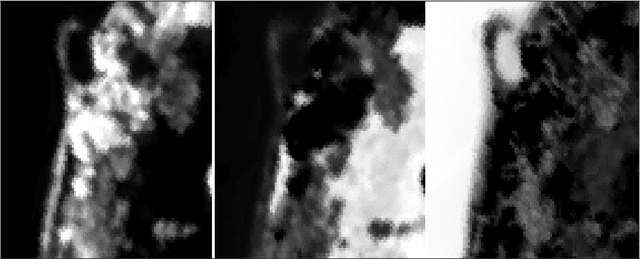
Simplex-structured matrix factorization (SSMF) is a generalization of nonnegative matrix factorization, a fundamental interpretable data analysis model, and has applications in hyperspectral unmixing and topic modeling. To obtain identifiable solutions, a standard approach is to find minimum-volume solutions. By taking advantage of the duality/polarity concept for polytopes, we convert minimum-volume SSMF in the primal space to a maximum-volume problem in the dual space. We first prove the identifiability of this maximum-volume dual problem. Then, we use this dual formulation to provide a novel optimization approach which bridges the gap between two existing families of algorithms for SSMF, namely volume minimization and facet identification. Numerical experiments show that the proposed approach performs favorably compared to the state-of-the-art SSMF algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge