Giovanni Barbarino
Robustness of Minimum-Volume Nonnegative Matrix Factorization under an Expanded Sufficiently Scattered Condition
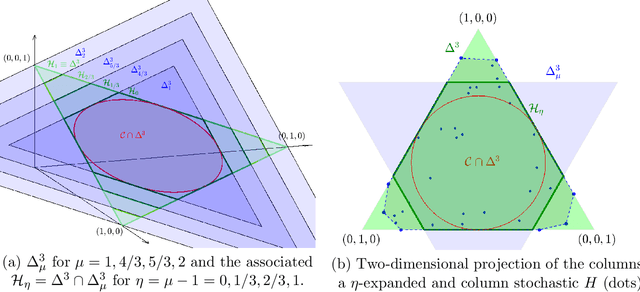
Nov 06, 2025Abstract:Minimum-volume nonnegative matrix factorization (min-vol NMF) has been used successfully in many applications, such as hyperspectral imaging, chemical kinetics, spectroscopy, topic modeling, and audio source separation. However, its robustness to noise has been a long-standing open problem. In this paper, we prove that min-vol NMF identifies the groundtruth factors in the presence of noise under a condition referred to as the expanded sufficiently scattered condition which requires the data points to be sufficiently well scattered in the latent simplex generated by the basis vectors.
Identifiability of Nonnegative Tucker Decompositions -- Part I: Theory
May 19, 2025


Abstract:Tensor decompositions have become a central tool in data science, with applications in areas such as data analysis, signal processing, and machine learning. A key property of many tensor decompositions, such as the canonical polyadic decomposition, is identifiability: the factors are unique, up to trivial scaling and permutation ambiguities. This allows one to recover the groundtruth sources that generated the data. The Tucker decomposition (TD) is a central and widely used tensor decomposition model. However, it is in general not identifiable. In this paper, we study the identifiability of the nonnegative TD (nTD). By adapting and extending identifiability results of nonnegative matrix factorization (NMF), we provide uniqueness results for nTD. Our results require the nonnegative matrix factors to have some degree of sparsity (namely, satisfy the separability condition, or the sufficiently scattered condition), while the core tensor only needs to have some slices (or linear combinations of them) or unfoldings with full column rank (but does not need to be nonnegative). Under such conditions, we derive several procedures, using either unfoldings or slices of the input tensor, to obtain identifiable nTDs by minimizing the volume of unfoldings or slices of the core tensor.
On the Robustness of the Successive Projection Algorithm
Nov 25, 2024



Abstract:The successive projection algorithm (SPA) is a workhorse algorithm to learn the $r$ vertices of the convex hull of a set of $(r-1)$-dimensional data points, a.k.a. a latent simplex, which has numerous applications in data science. In this paper, we revisit the robustness to noise of SPA and several of its variants. In particular, when $r \geq 3$, we prove the tightness of the existing error bounds for SPA and for two more robust preconditioned variants of SPA. We also provide significantly improved error bounds for SPA, by a factor proportional to the conditioning of the $r$ vertices, in two special cases: for the first extracted vertex, and when $r \leq 2$. We then provide further improvements for the error bounds of a translated version of SPA proposed by Arora et al. (''A practical algorithm for topic modeling with provable guarantees'', ICML, 2013) in two special cases: for the first two extracted vertices, and when $r \leq 3$. Finally, we propose a new more robust variant of SPA that first shifts and lifts the data points in order to minimize the conditioning of the problem. We illustrate our results on synthetic data.
Dual Simplex Volume Maximization for Simplex-Structured Matrix Factorization
Mar 29, 2024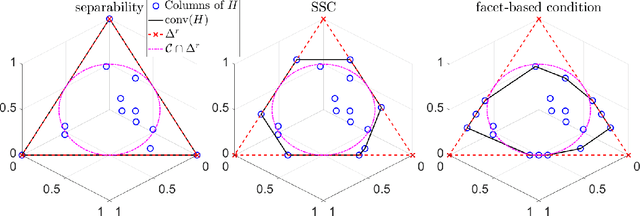
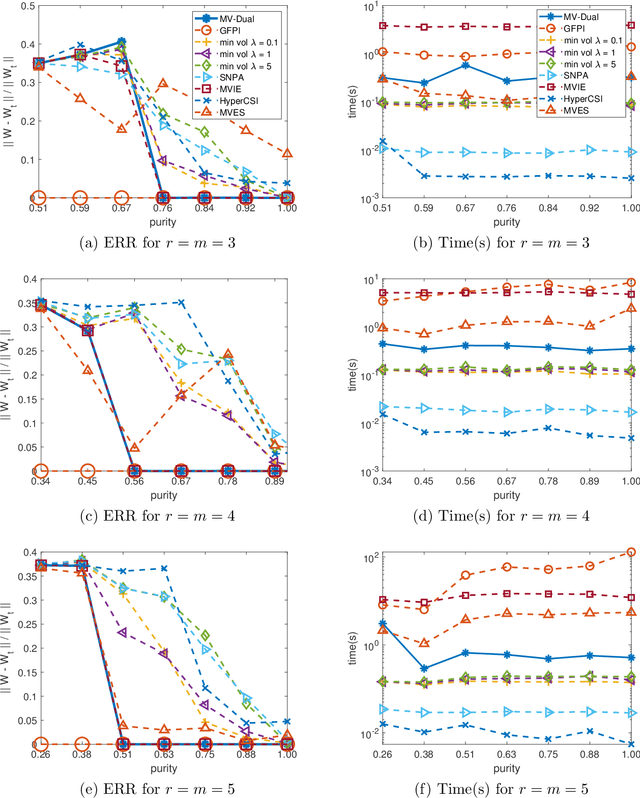
Abstract:Simplex-structured matrix factorization (SSMF) is a generalization of nonnegative matrix factorization, a fundamental interpretable data analysis model, and has applications in hyperspectral unmixing and topic modeling. To obtain identifiable solutions, a standard approach is to find minimum-volume solutions. By taking advantage of the duality/polarity concept for polytopes, we convert minimum-volume SSMF in the primal space to a maximum-volume problem in the dual space. We first prove the identifiability of this maximum-volume dual problem. Then, we use this dual formulation to provide a novel optimization approach which bridges the gap between two existing families of algorithms for SSMF, namely volume minimization and facet identification. Numerical experiments show that the proposed approach performs favorably compared to the state-of-the-art SSMF algorithms.
Permutation NMF
Aug 03, 2016

Abstract:Nonnegative Matrix Factorization(NMF) is a common used technique in machine learning to extract features out of data such as text documents and images thanks to its natural clustering properties. In particular, it is popular in image processing since it can decompose several pictures and recognize common parts if they're located in the same position over the photos. This paper's aim is to present a way to add the translation invariance to the classical NMF, that is, the algorithms presented are able to detect common features, even when they're shifted, in different original images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge