Dual Simplex Volume Maximization for Simplex-Structured Matrix Factorization

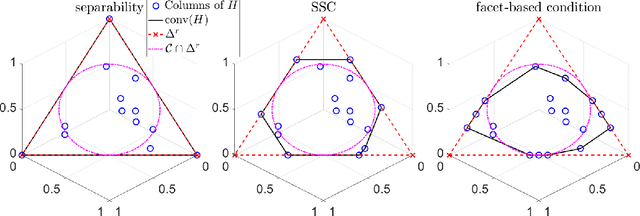
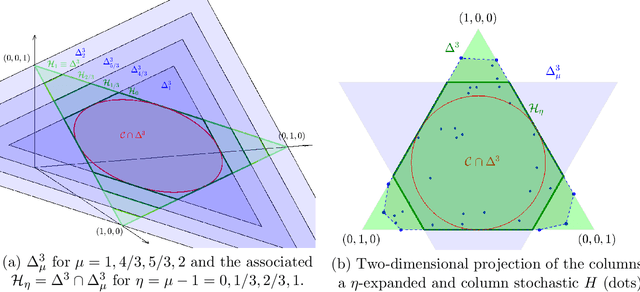
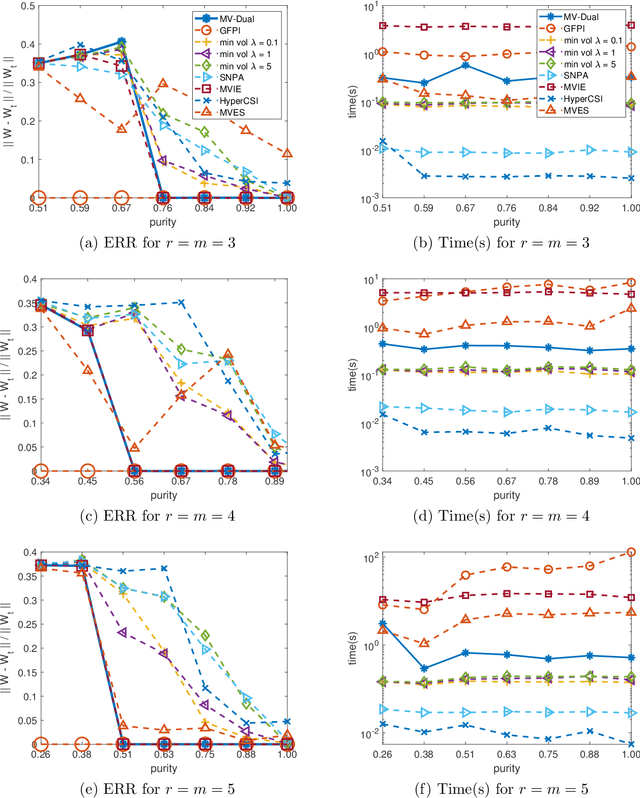
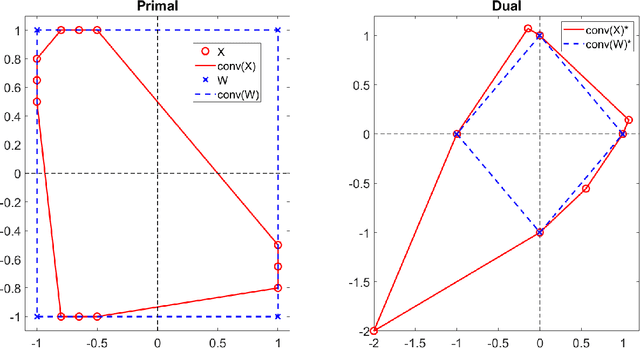
Simplex-structured matrix factorization (SSMF) is a generalization of nonnegative matrix factorization, a fundamental interpretable data analysis model, and has applications in hyperspectral unmixing and topic modeling. To obtain identifiable solutions, a standard approach is to find minimum-volume solutions. By taking advantage of the duality/polarity concept for polytopes, we convert minimum-volume SSMF in the primal space to a maximum-volume problem in the dual space. We first prove the identifiability of this maximum-volume dual problem. Then, we use this dual formulation to provide a novel optimization approach which bridges the gap between two existing families of algorithms for SSMF, namely volume minimization and facet identification. Numerical experiments show that the proposed approach performs favorably compared to the state-of-the-art SSMF algorithms.

Revisiting data augmentation for subspace clustering

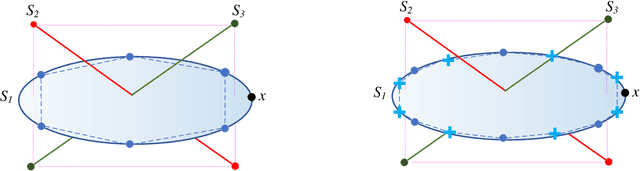
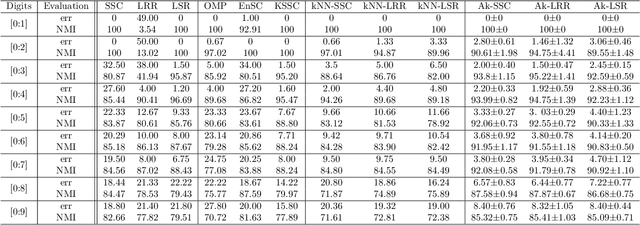
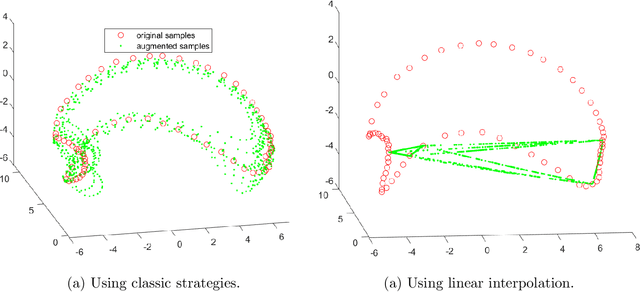
Subspace clustering is the classical problem of clustering a collection of data samples that approximately lie around several low-dimensional subspaces. The current state-of-the-art approaches for this problem are based on the self-expressive model which represents the samples as linear combination of other samples. However, these approaches require sufficiently well-spread samples for accurate representation which might not be necessarily accessible in many applications. In this paper, we shed light on this commonly neglected issue and argue that data distribution within each subspace plays a critical role in the success of self-expressive models. Our proposed solution to tackle this issue is motivated by the central role of data augmentation in the generalization power of deep neural networks. We propose two subspace clustering frameworks for both unsupervised and semi-supervised settings that use augmented samples as an enlarged dictionary to improve the quality of the self-expressive representation. We present an automatic augmentation strategy using a few labeled samples for the semi-supervised problem relying on the fact that the data samples lie in the union of multiple linear subspaces. Experimental results confirm the effectiveness of data augmentation, as it significantly improves the performance of general self-expressive models.

Beyond Linear Subspace Clustering: A Comparative Study of Nonlinear Manifold Clustering Algorithms

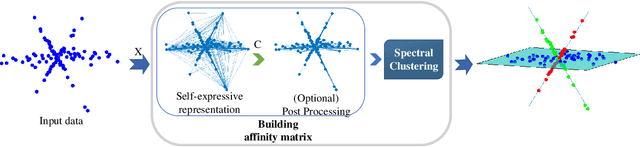
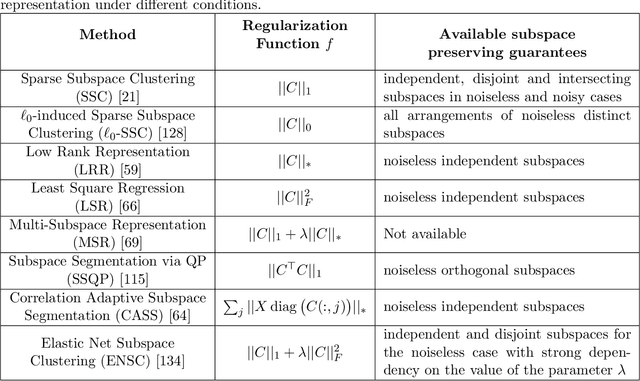
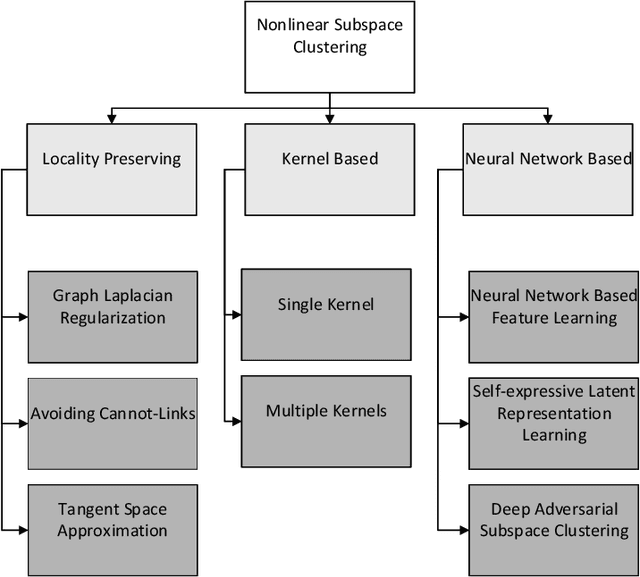
Subspace clustering is an important unsupervised clustering approach. It is based on the assumption that the high-dimensional data points are approximately distributed around several low-dimensional linear subspaces. The majority of the prominent subspace clustering algorithms rely on the representation of the data points as linear combinations of other data points, which is known as a self-expressive representation. To overcome the restrictive linearity assumption, numerous nonlinear approaches were proposed to extend successful subspace clustering approaches to data on a union of nonlinear manifolds. In this comparative study, we provide a comprehensive overview of nonlinear subspace clustering approaches proposed in the last decade. We introduce a new taxonomy to classify the state-of-the-art approaches into three categories, namely locality preserving, kernel based, and neural network based. The major representative algorithms within each category are extensively compared on carefully designed synthetic and real-world data sets. The detailed analysis of these approaches unfolds potential research directions and unsolved challenges in this field.

Simplex-Structured Matrix Factorization: Sparsity-based Identifiability and Provably Correct Algorithms

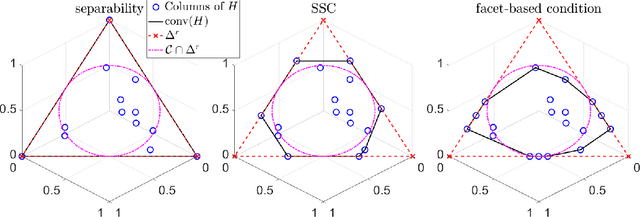
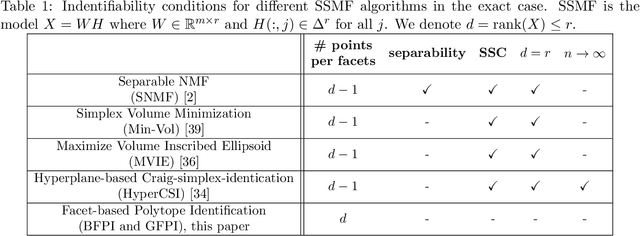
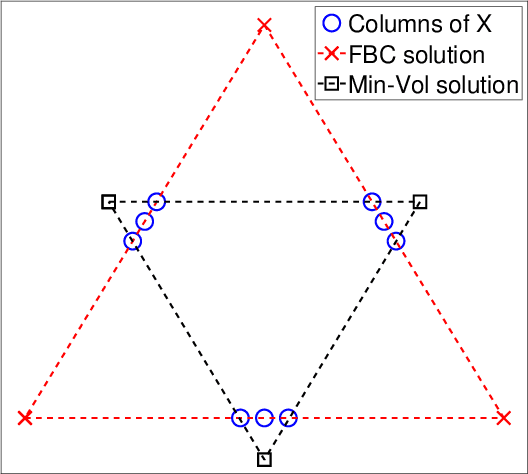
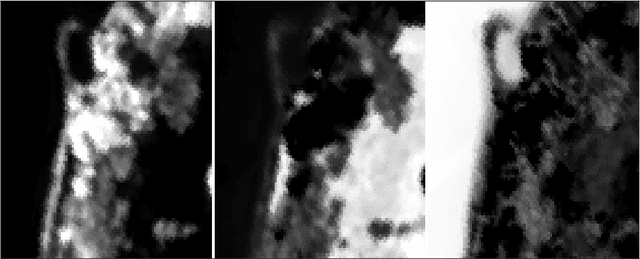
In this paper, we provide novel algorithms with identifiability guarantees for simplex-structured matrix factorization (SSMF), a generalization of nonnegative matrix factorization. Current state-of-the-art algorithms that provide identifiability results for SSMF rely on the sufficiently scattered condition (SSC) which requires the data points to be well spread within the convex hull of the basis vectors. The conditions under which our proposed algorithms recover the unique decomposition is in most cases much weaker than the SSC. We only require to have $d$ points on each facet of the convex hull of the basis vectors whose dimension is $d-1$. The key idea is based on extracting facets containing the largest number of points. We illustrate the effectiveness of our approach on synthetic data sets and hyperspectral images, showing that it outperforms state-of-the-art SSMF algorithms as it is able to handle higher noise levels, rank deficient matrices, outliers, and input data that highly violates the SSC.

Neither Global Nor Local: A Hierarchical Robust Subspace Clustering For Image Data

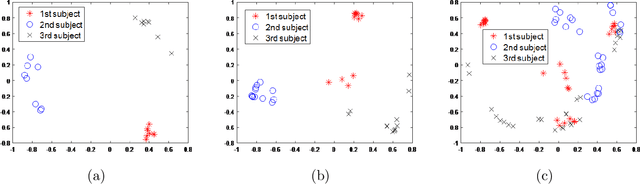
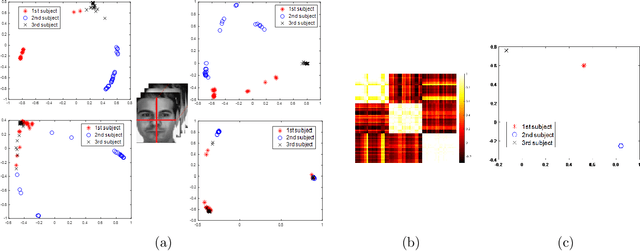
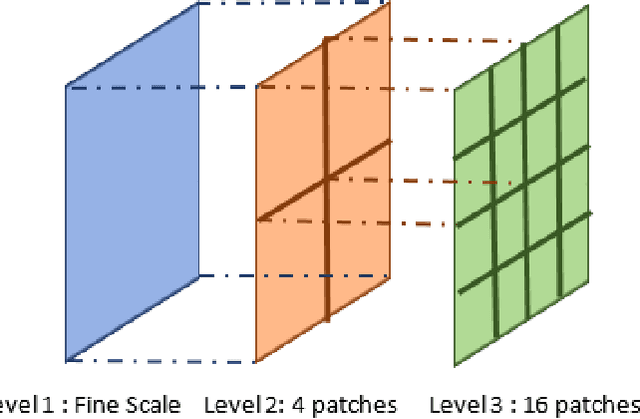
In this paper, we consider the problem of subspace clustering in presence of contiguous noise, occlusion and disguise. We argue that self-expressive representation of data in current state-of-the-art approaches is severely sensitive to occlusions and complex real-world noises. To alleviate this problem, we propose a hierarchical framework that brings robustness of local patches-based representations and discriminant property of global representations together. This approach consists of 1) a top-down stage, in which the input data is subject to repeated division to smaller patches and 2) a bottom-up stage, in which the low rank embedding of local patches in field of view of a corresponding patch in upper level are merged on a Grassmann manifold. This summarized information provides two key information for the corresponding patch on the upper level: cannot-links and recommended-links. This information is employed for computing a self-expressive representation of each patch at upper levels using a weighted sparse group lasso optimization problem. Numerical results on several real data sets confirm the efficiency of our approach.

Scalable and Robust Sparse Subspace Clustering Using Randomized Clustering and Multilayer Graphs

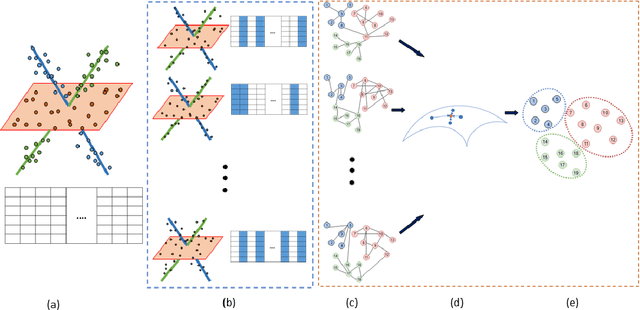
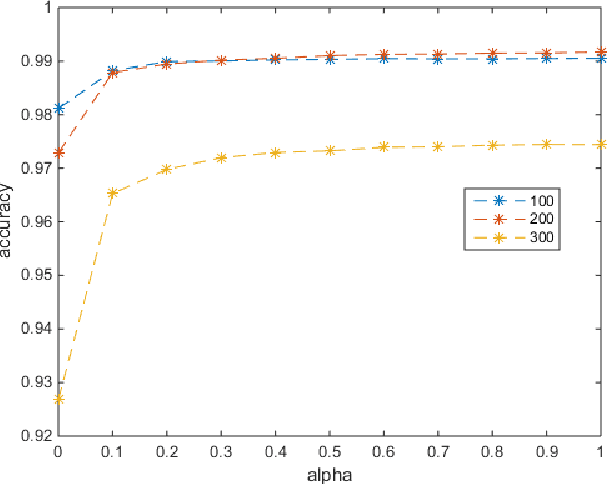
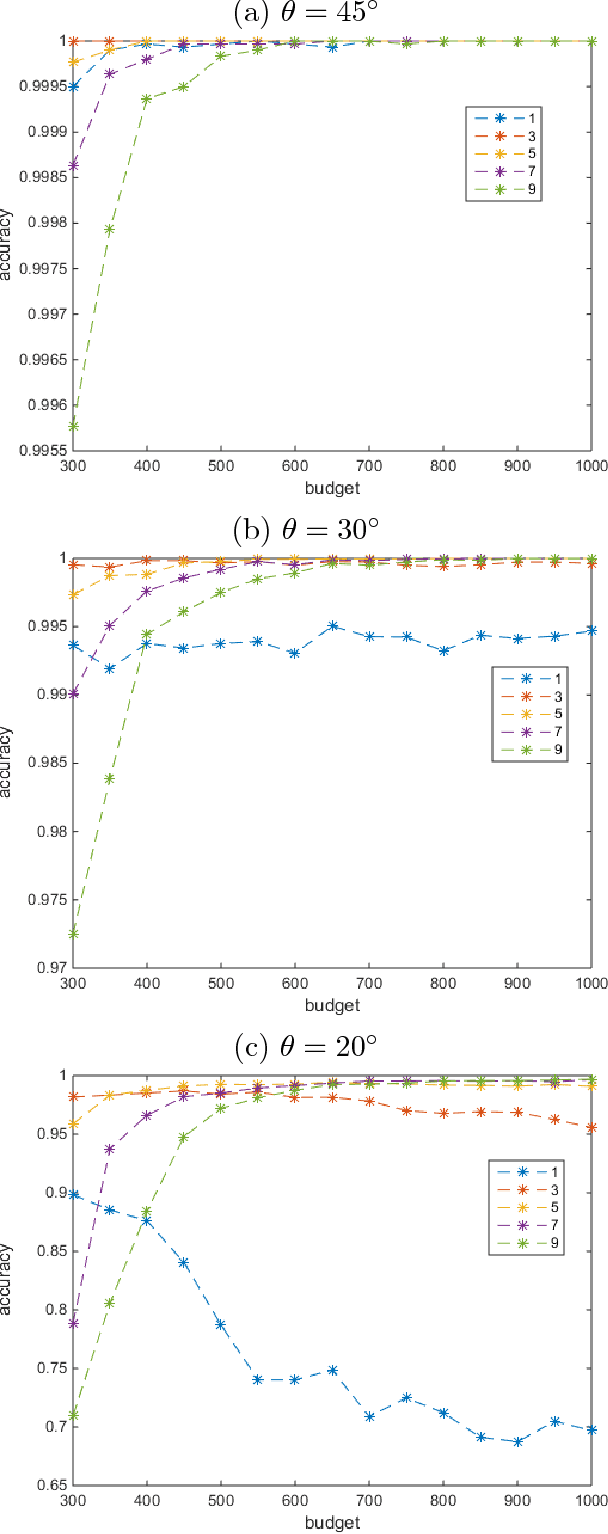
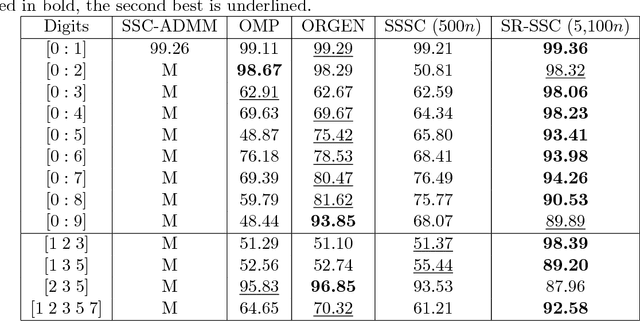
Sparse subspace clustering (SSC) is one of the current state-of-the-art methods for partitioning data points into the union of subspaces, with strong theoretical guarantees. However, it is not practical for large data sets as it requires solving a LASSO problem for each data point, where the number of variables in each LASSO problem is the number of data points. To improve the scalability of SSC, we propose to select a few sets of anchor points using a randomized hierarchical clustering method, and, for each set of anchor points, solve the LASSO problems for each data point allowing only anchor points to have a non-zero weight (this reduces drastically the number of variables). This generates a multilayer graph where each layer corresponds to a different set of anchor points. Using the Grassmann manifold of orthogonal matrices, the shared connectivity among the layers is summarized within a single subspace. Finally, we use $k$-means clustering within that subspace to cluster the data points, similarly as done by spectral clustering in SSC. We show on both synthetic and real-world data sets that the proposed method not only allows SSC to scale to large-scale data sets, but that it is also much more robust as it performs significantly better on noisy data and on data with close susbspaces and outliers, while it is not prone to oversegmentation.