Simplex-Structured Matrix Factorization: Sparsity-based Identifiability and Provably Correct Algorithms
Paper and Code
Jul 22, 2020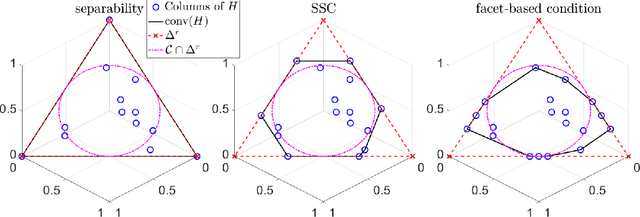
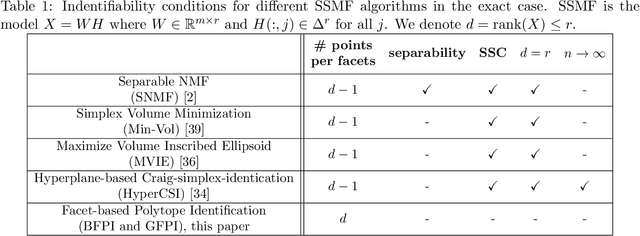
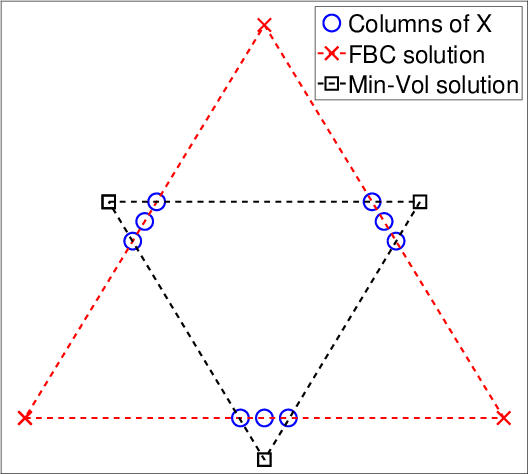
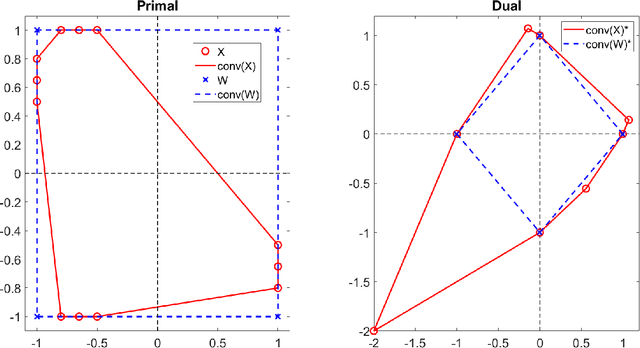
In this paper, we provide novel algorithms with identifiability guarantees for simplex-structured matrix factorization (SSMF), a generalization of nonnegative matrix factorization. Current state-of-the-art algorithms that provide identifiability results for SSMF rely on the sufficiently scattered condition (SSC) which requires the data points to be well spread within the convex hull of the basis vectors. The conditions under which our proposed algorithms recover the unique decomposition is in most cases much weaker than the SSC. We only require to have $d$ points on each facet of the convex hull of the basis vectors whose dimension is $d-1$. The key idea is based on extracting facets containing the largest number of points. We illustrate the effectiveness of our approach on synthetic data sets and hyperspectral images, showing that it outperforms state-of-the-art SSMF algorithms as it is able to handle higher noise levels, rank deficient matrices, outliers, and input data that highly violates the SSC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge