Scalable and Robust Sparse Subspace Clustering Using Randomized Clustering and Multilayer Graphs
Paper and Code
Feb 23, 2018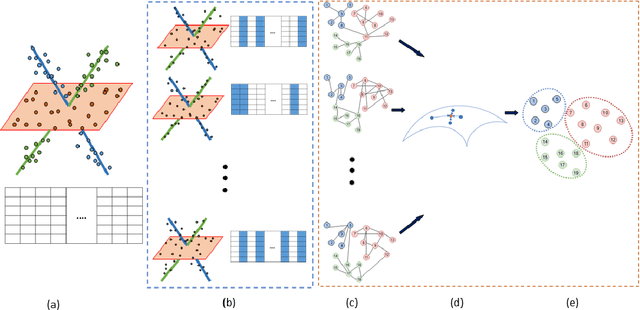
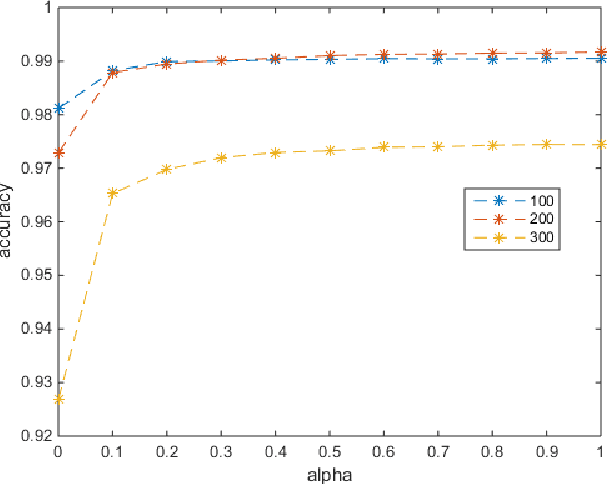
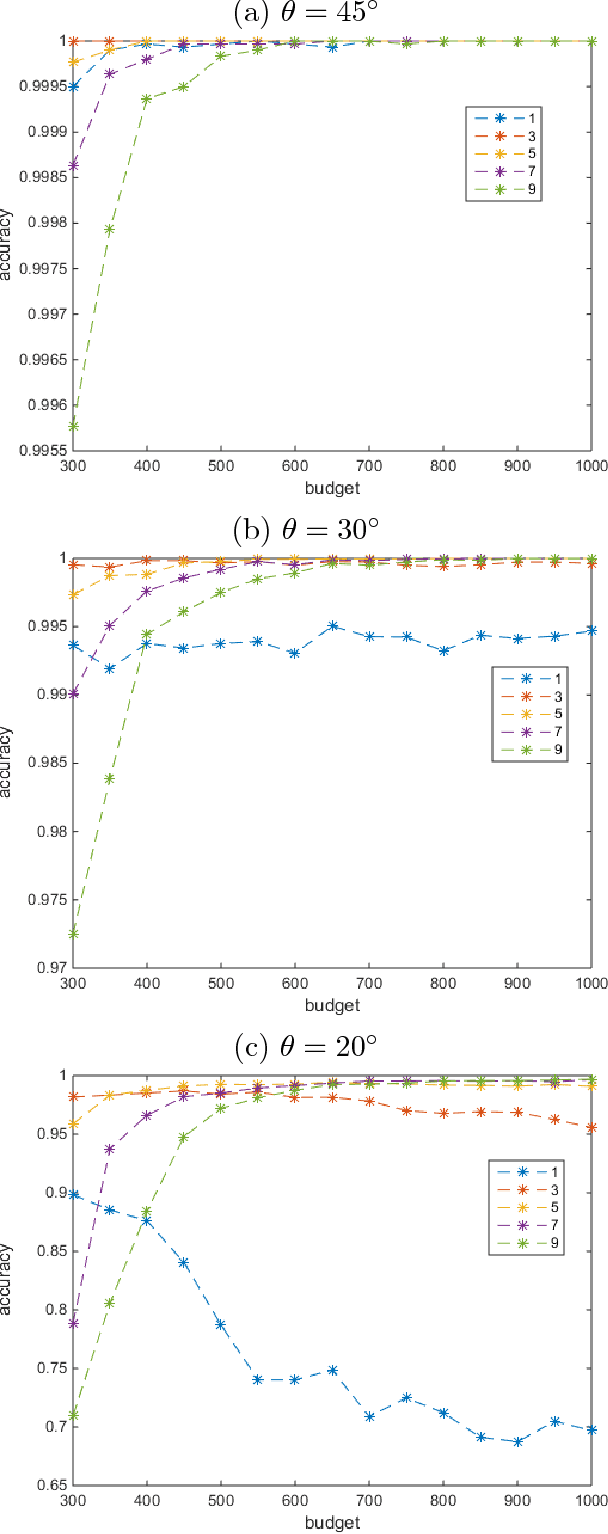
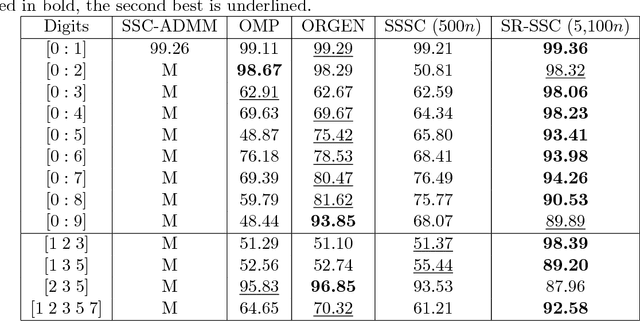
Sparse subspace clustering (SSC) is one of the current state-of-the-art methods for partitioning data points into the union of subspaces, with strong theoretical guarantees. However, it is not practical for large data sets as it requires solving a LASSO problem for each data point, where the number of variables in each LASSO problem is the number of data points. To improve the scalability of SSC, we propose to select a few sets of anchor points using a randomized hierarchical clustering method, and, for each set of anchor points, solve the LASSO problems for each data point allowing only anchor points to have a non-zero weight (this reduces drastically the number of variables). This generates a multilayer graph where each layer corresponds to a different set of anchor points. Using the Grassmann manifold of orthogonal matrices, the shared connectivity among the layers is summarized within a single subspace. Finally, we use $k$-means clustering within that subspace to cluster the data points, similarly as done by spectral clustering in SSC. We show on both synthetic and real-world data sets that the proposed method not only allows SSC to scale to large-scale data sets, but that it is also much more robust as it performs significantly better on noisy data and on data with close susbspaces and outliers, while it is not prone to oversegmentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge