Orthogonal Nonnegative Matrix Factorization with the Kullback-Leibler divergence
Paper and Code
Oct 10, 2024
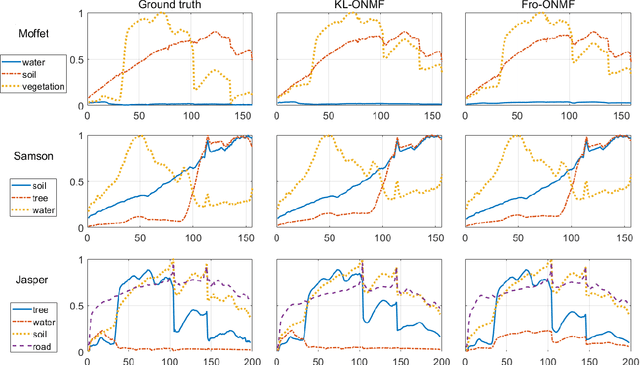


Orthogonal nonnegative matrix factorization (ONMF) has become a standard approach for clustering. As far as we know, most works on ONMF rely on the Frobenius norm to assess the quality of the approximation. This paper presents a new model and algorithm for ONMF that minimizes the Kullback-Leibler (KL) divergence. As opposed to the Frobenius norm which assumes Gaussian noise, the KL divergence is the maximum likelihood estimator for Poisson-distributed data, which can model better vectors of word counts in document data sets and photo counting processes in imaging. We have developed an algorithm based on alternating optimization, KL-ONMF, and show that it performs favorably with the Frobenius-norm based ONMF for document classification and hyperspectral image unmixing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge