Deep learning methods for inverse problems using connections between proximal operators and Hamilton-Jacobi equations

Inverse problems are important mathematical problems that seek to recover model parameters from noisy data. Since inverse problems are often ill-posed, they require regularization or incorporation of prior information about the underlying model or unknown variables. Proximal operators, ubiquitous in nonsmooth optimization, are central to this because they provide a flexible and convenient way to encode priors and build efficient iterative algorithms. They have also recently become key to modern machine learning methods, e.g., for plug-and-play methods for learned denoisers and deep neural architectures for learning priors of proximal operators. The latter was developed partly due to recent work characterizing proximal operators of nonconvex priors as subdifferential of convex potentials. In this work, we propose to leverage connections between proximal operators and Hamilton-Jacobi partial differential equations (HJ PDEs) to develop novel deep learning architectures for learning the prior. In contrast to other existing methods, we learn the prior directly without recourse to inverting the prior after training. We present several numerical results that demonstrate the efficiency of the proposed method in high dimensions.

Momentum-based minimization of the Ginzburg-Landau functional on Euclidean spaces and graphs

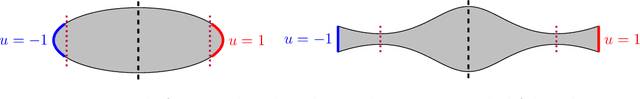
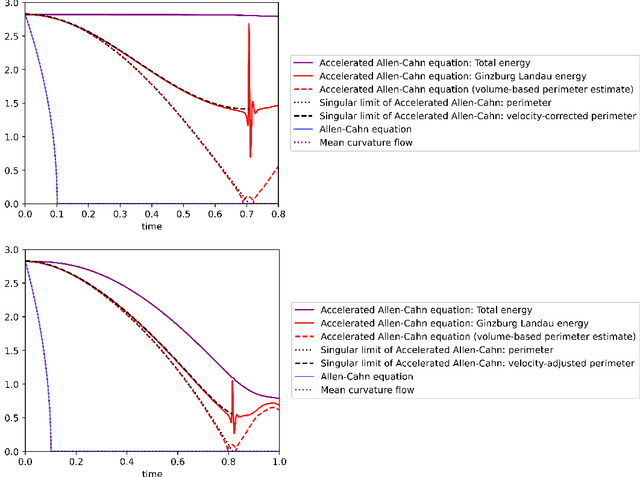
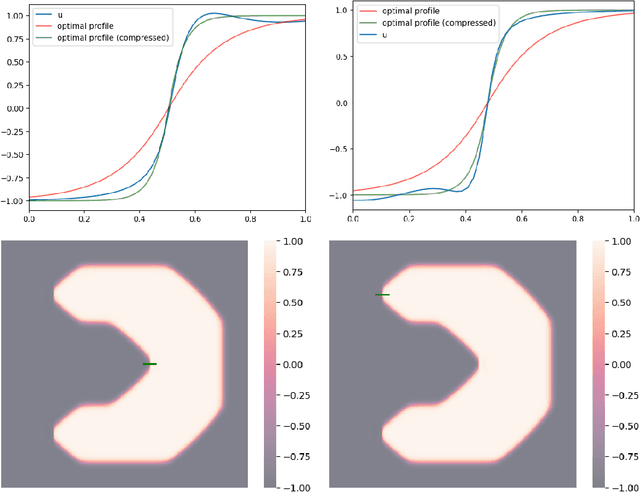
We study the momentum-based minimization of a diffuse perimeter functional on Euclidean spaces and on graphs with applications to semi-supervised classification tasks in machine learning. While the gradient flow in the task at hand is a parabolic partial differential equation, the momentum-method corresponds to a damped hyperbolic PDE, leading to qualitatively and quantitatively different trajectories. Using a convex-concave splitting-based FISTA-type time discretization, we demonstrate empirically that momentum can lead to faster convergence if the time step size is large but not too large. With large time steps, the PDE analysis offers only limited insight into the geometric behavior of solutions and typical hyperbolic phenomena like loss of regularity are not be observed in sample simulations.

Deep Nonnegative Matrix Factorization with Beta Divergences

Deep Nonnegative Matrix Factorization (deep NMF) has recently emerged as a valuable technique for extracting multiple layers of features across different scales. However, all existing deep NMF models and algorithms have primarily centered their evaluation on the least squares error, which may not be the most appropriate metric for assessing the quality of approximations on diverse datasets. For instance, when dealing with data types such as audio signals and documents, it is widely acknowledged that $\beta$-divergences offer a more suitable alternative. In this paper, we develop new models and algorithms for deep NMF using $\beta$-divergences. Subsequently, we apply these techniques to the extraction of facial features, the identification of topics within document collections, and the identification of materials within hyperspectral images.

Novel Deep neural networks for solving Bayesian statistical inverse

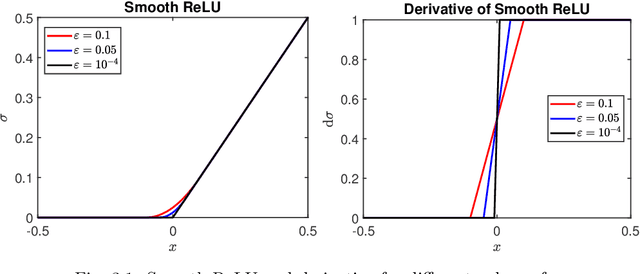
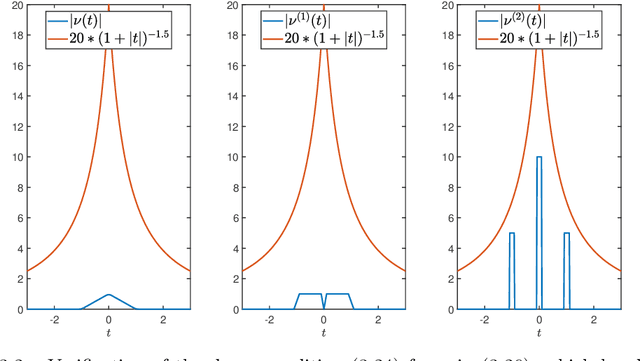
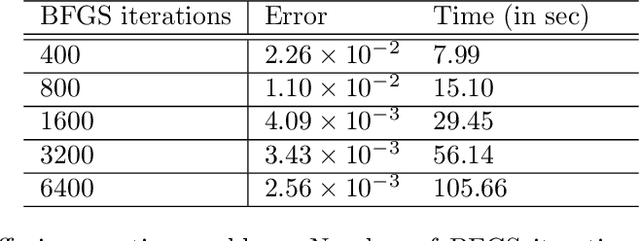
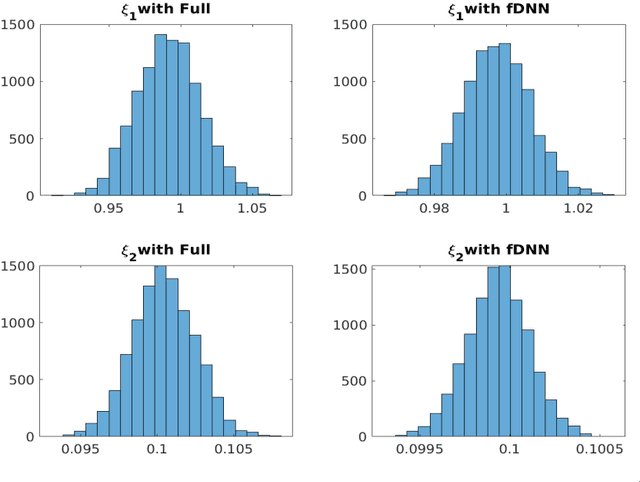
We consider the simulation of Bayesian statistical inverse problems governed by large-scale linear and nonlinear partial differential equations (PDEs). Markov chain Monte Carlo (MCMC) algorithms are standard techniques to solve such problems. However, MCMC techniques are computationally challenging as they require several thousands of forward PDE solves. The goal of this paper is to introduce a fractional deep neural network based approach for the forward solves within an MCMC routine. Moreover, we discuss some approximation error estimates and illustrate the efficiency of our approach via several numerical examples.