Block Majorization Minimization with Extrapolation and Application to $β$-NMF

We propose a Block Majorization Minimization method with Extrapolation (BMMe) for solving a class of multi-convex optimization problems. The extrapolation parameters of BMMe are updated using a novel adaptive update rule. By showing that block majorization minimization can be reformulated as a block mirror descent method, with the Bregman divergence adaptively updated at each iteration, we establish subsequential convergence for BMMe. We use this method to design efficient algorithms to tackle nonnegative matrix factorization problems with the $\beta$-divergences ($\beta$-NMF) for $\beta\in [1,2]$. These algorithms, which are multiplicative updates with extrapolation, benefit from our novel results that offer convergence guarantees. We also empirically illustrate the significant acceleration of BMMe for $\beta$-NMF through extensive experiments.

Deep Nonnegative Matrix Factorization with Beta Divergences

Deep Nonnegative Matrix Factorization (deep NMF) has recently emerged as a valuable technique for extracting multiple layers of features across different scales. However, all existing deep NMF models and algorithms have primarily centered their evaluation on the least squares error, which may not be the most appropriate metric for assessing the quality of approximations on diverse datasets. For instance, when dealing with data types such as audio signals and documents, it is widely acknowledged that $\beta$-divergences offer a more suitable alternative. In this paper, we develop new models and algorithms for deep NMF using $\beta$-divergences. Subsequently, we apply these techniques to the extraction of facial features, the identification of topics within document collections, and the identification of materials within hyperspectral images.

Anomaly detection with semi-supervised classification based on risk estimators

A significant limitation of one-class classification anomaly detection methods is their reliance on the assumption that unlabeled training data only contains normal instances. To overcome this impractical assumption, we propose two novel classification-based anomaly detection methods. Firstly, we introduce a semi-supervised shallow anomaly detection method based on an unbiased risk estimator. Secondly, we present a semi-supervised deep anomaly detection method utilizing a nonnegative (biased) risk estimator. We establish estimation error bounds and excess risk bounds for both risk minimizers. Additionally, we propose techniques to select appropriate regularization parameters that ensure the nonnegativity of the empirical risk in the shallow model under specific loss functions. Our extensive experiments provide strong evidence of the effectiveness of the risk-based anomaly detection methods.

Multiblock ADMM for nonsmooth nonconvex optimization with nonlinear coupling constraints

This paper considers a multiblock nonsmooth nonconvex optimization problem with nonlinear coupling constraints. By developing the idea of using the information zone and adaptive regime proposed in [J. Bolte, S. Sabach and M. Teboulle, Nonconvex Lagrangian-based optimization: Monitoring schemes and global convergence, Mathematics of Operations Research, 43: 1210--1232, 2018], we propose a multiblock alternating direction method of multipliers for solving this problem. We specify the update of the primal variables by employing a majorization minimization procedure in each block update. An independent convergence analysis is conducted to prove subsequential as well as global convergence of the generated sequence to a critical point of the augmented Lagrangian. We also establish iteration complexity and provide preliminary numerical results for the proposed algorithm.

Block Alternating Bregman Majorization Minimization with Extrapolation

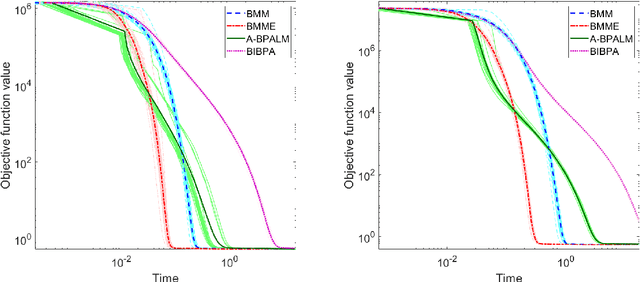
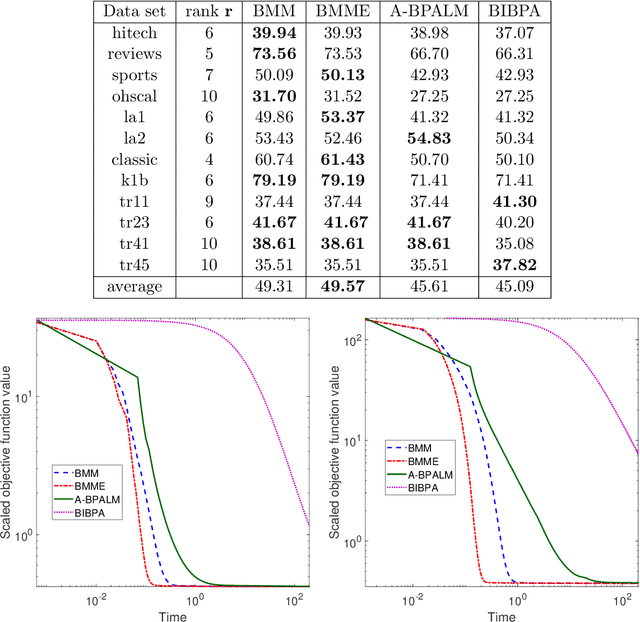
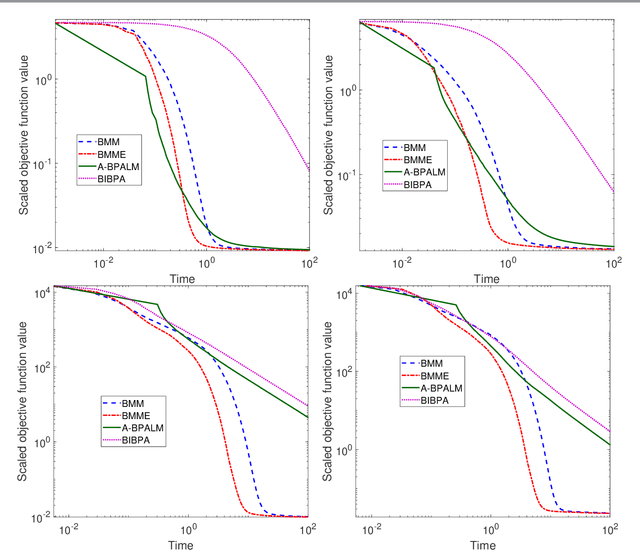
In this paper, we consider a class of nonsmooth nonconvex optimization problems whose objective is the sum of a block relative smooth function and a proper and lower semicontinuous block separable function. Although the analysis of block proximal gradient (BPG) methods for the class of block $L$-smooth functions have been successfully extended to Bregman BPG methods that deal with the class of block relative smooth functions, accelerated Bregman BPG methods are scarce and challenging to design. Taking our inspiration from Nesterov-type acceleration and the majorization-minimization scheme, we propose a block alternating Bregman Majorization-Minimization framework with Extrapolation (BMME). We prove subsequential convergence of BMME to a first-order stationary point under mild assumptions, and study its global convergence under stronger conditions. We illustrate the effectiveness of BMME on the penalized orthogonal nonnegative matrix factorization problem.

A Framework of Inertial Alternating Direction Method of Multipliers for Non-Convex Non-Smooth Optimization

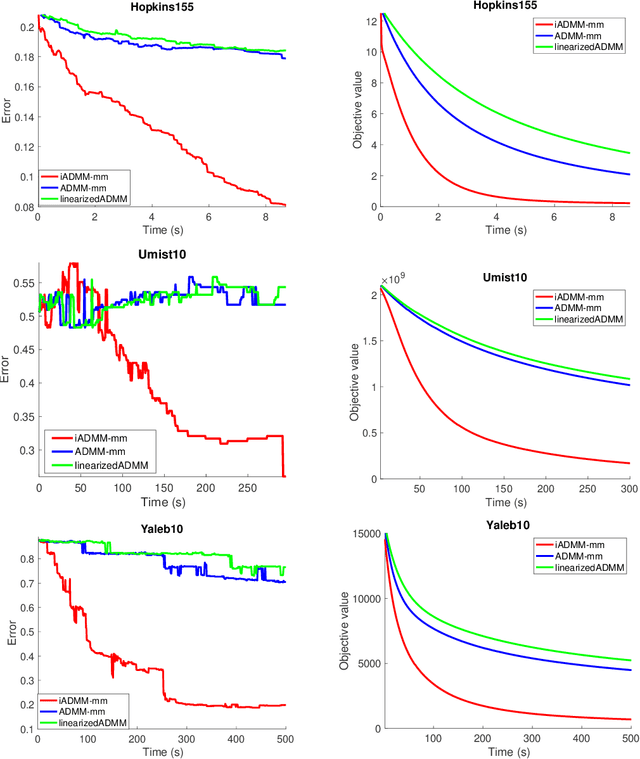
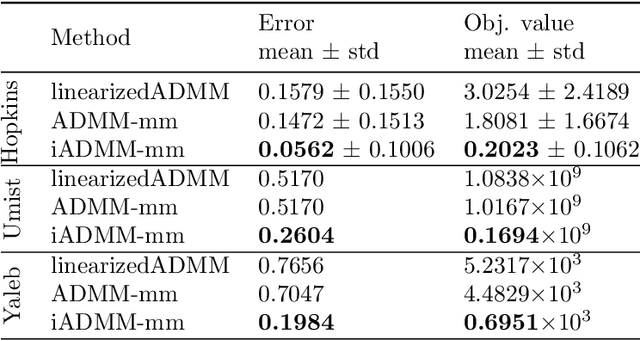
In this paper, we propose an algorithmic framework dubbed inertial alternating direction methods of multipliers (iADMM), for solving a class of nonconvex nonsmooth multiblock composite optimization problems with linear constraints. Our framework employs the general minimization-majorization (MM) principle to update each block of variables so as to not only unify the convergence analysis of previous ADMM that use specific surrogate functions in the MM step, but also lead to new efficient ADMM schemes. To the best of our knowledge, in the \emph{nonconvex nonsmooth} setting, ADMM used in combination with the MM principle to update each block of variables, and ADMM combined with inertial terms for the primal variables have not been studied in the literature. Under standard assumptions, we prove the subsequential convergence and global convergence for the generated sequence of iterates. We illustrate the effectiveness of iADMM on a class of nonconvex low-rank representation problems.

An Inertial Block Majorization Minimization Framework for Nonsmooth Nonconvex Optimization

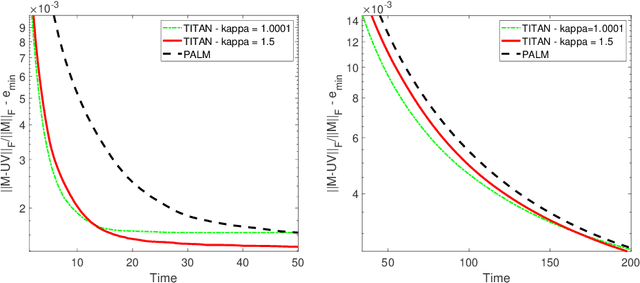
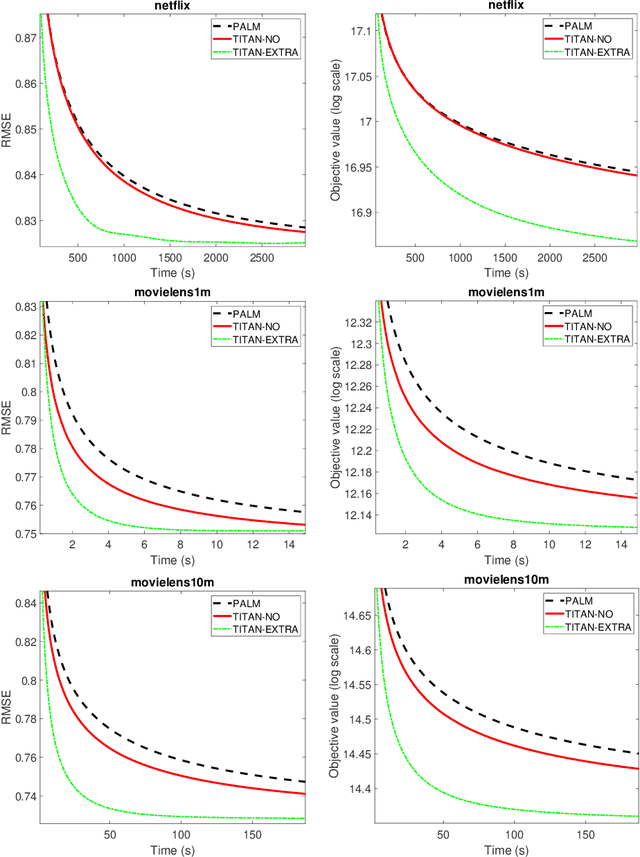
In this paper, we introduce TITAN, a novel inerTial block majorIzation minimization framework for non-smooth non-convex opTimizAtioN problems. TITAN is a block coordinate method (BCM) that embeds inertial force to each majorization-minimization step of the block updates. The inertial force is obtained via an extrapolation operator that subsumes heavy-ball and Nesterov-type accelerations for block proximal gradient methods as special cases. By choosing various surrogate functions, such as proximal, Lipschitz gradient, Bregman, quadratic, and composite surrogate functions, and by varying the extrapolation operator, TITAN produces a rich set of inertial BCMs. We study sub-sequential convergence as well as global convergence for the generated sequence of TITAN. We illustrate the effectiveness of TITAN on two important machine learning problems, namely sparse non-negative matrix factorization and matrix completion.

Algorithms for Nonnegative Matrix Factorization with the Kullback-Leibler Divergence

Nonnegative matrix factorization (NMF) is a standard linear dimensionality reduction technique for nonnegative data sets. In order to measure the discrepancy between the input data and the low-rank approximation, the Kullback-Leibler (KL) divergence is one of the most widely used objective function for NMF. It corresponds to the maximum likehood estimator when the underlying statistics of the observed data sample follows a Poisson distribution, and KL NMF is particularly meaningful for count data sets, such as documents or images. In this paper, we first collect important properties of the KL objective function that are essential to study the convergence of KL NMF algorithms. Second, together with reviewing existing algorithms for solving KL NMF, we propose three new algorithms that guarantee the non-increasingness of the objective function. We also provide a global convergence guarantee for one of our proposed algorithms. Finally, we conduct extensive numerical experiments to provide a comprehensive picture of the performances of the KL NMF algorithms.

Accelerating Block Coordinate Descent for Nonnegative Tensor Factorization

This paper is concerned with improving the empirical convergence speed of block-coordinate descent algorithms for approximate nonnegative tensor factorization (NTF). We propose an extrapolation strategy in-between block updates, referred to as heuristic extrapolation with restarts (HER). HER significantly accelerates the empirical convergence speed of most existing block-coordinate algorithms for dense NTF, in particular for challenging computational scenarios, while requiring a negligible additional computational budget.

Inertial Block Mirror Descent Method for Non-Convex Non-Smooth Optimization

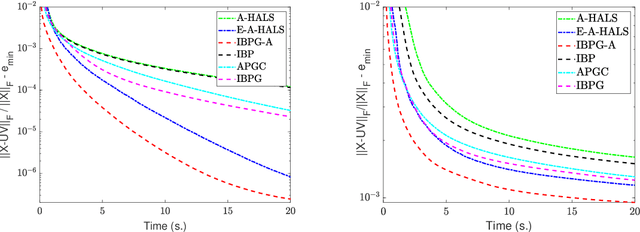
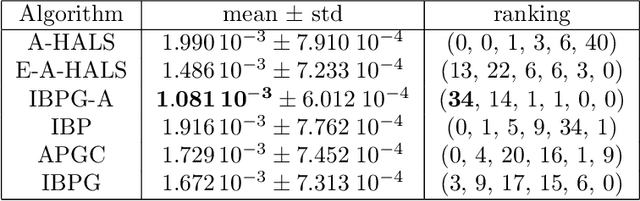
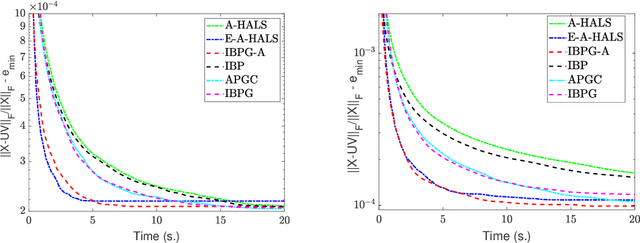
In this paper, we propose inertial versions of block coordinate descent methods for solving non-convex non-smooth composite optimization problems. We use the general framework of Bregman distance functions to compute the proximal maps. Our method not only allows using two different extrapolation points to evaluate gradients and adding the inertial force, but also takes advantage of randomly picking the block of variables to update. Moreover, our method does not require a restarting step, and as such, it is not a monotonically decreasing method. To prove the convergence of the whole generated sequence to a critical point, we modify the convergence proof recipe of Bolte, Sabach and Teboulle (Proximal alternating linearized minimization for non-convex and non-smooth problems, Math. Prog. 146(1):459--494, 2014), and combine it with auxiliary functions. We deploy the proposed methods to solve non-negative matrix factorization (NMF) problems and show that they compete favourably with the state-of-the-art NMF algorithms.