Matrix Completion via Nonsmooth Regularization of Fully Connected Neural Networks

Conventional matrix completion methods approximate the missing values by assuming the matrix to be low-rank, which leads to a linear approximation of missing values. It has been shown that enhanced performance could be attained by using nonlinear estimators such as deep neural networks. Deep fully connected neural networks (FCNNs), one of the most suitable architectures for matrix completion, suffer from over-fitting due to their high capacity, which leads to low generalizability. In this paper, we control over-fitting by regularizing the FCNN model in terms of the $\ell_{1}$ norm of intermediate representations and nuclear norm of weight matrices. As such, the resulting regularized objective function becomes nonsmooth and nonconvex, i.e., existing gradient-based methods cannot be applied to our model. We propose a variant of the proximal gradient method and investigate its convergence to a critical point. In the initial epochs of FCNN training, the regularization terms are ignored, and through epochs, the effect of that increases. The gradual addition of nonsmooth regularization terms is the main reason for the better performance of the deep neural network with nonsmooth regularization terms (DNN-NSR) algorithm. Our simulations indicate the superiority of the proposed algorithm in comparison with existing linear and nonlinear algorithms.

Block Alternating Bregman Majorization Minimization with Extrapolation

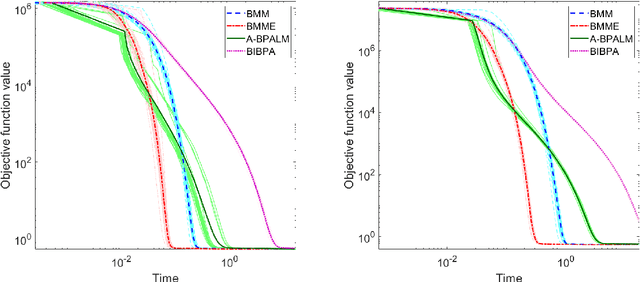
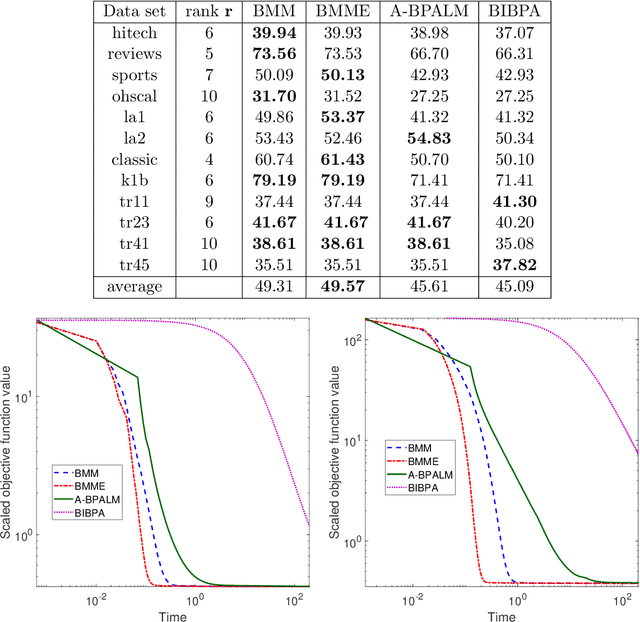
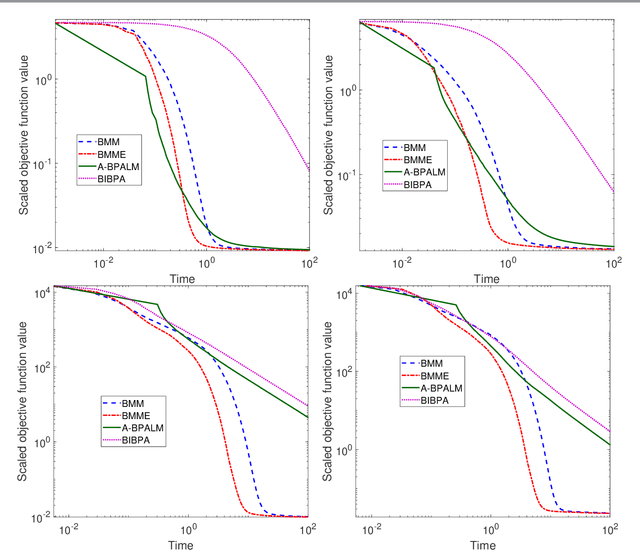
In this paper, we consider a class of nonsmooth nonconvex optimization problems whose objective is the sum of a block relative smooth function and a proper and lower semicontinuous block separable function. Although the analysis of block proximal gradient (BPG) methods for the class of block $L$-smooth functions have been successfully extended to Bregman BPG methods that deal with the class of block relative smooth functions, accelerated Bregman BPG methods are scarce and challenging to design. Taking our inspiration from Nesterov-type acceleration and the majorization-minimization scheme, we propose a block alternating Bregman Majorization-Minimization framework with Extrapolation (BMME). We prove subsequential convergence of BMME to a first-order stationary point under mild assumptions, and study its global convergence under stronger conditions. We illustrate the effectiveness of BMME on the penalized orthogonal nonnegative matrix factorization problem.