Scalable AI Framework for Defect Detection in Metal Additive Manufacturing

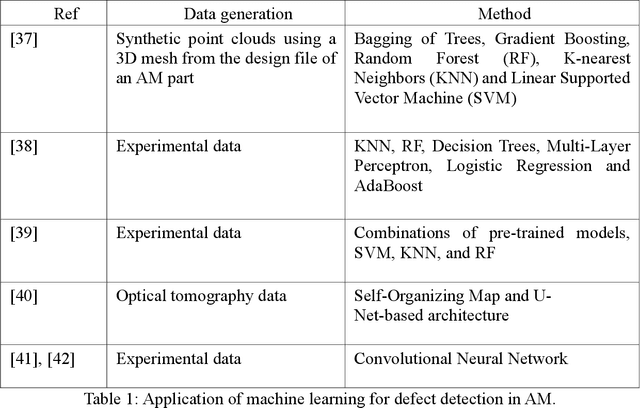
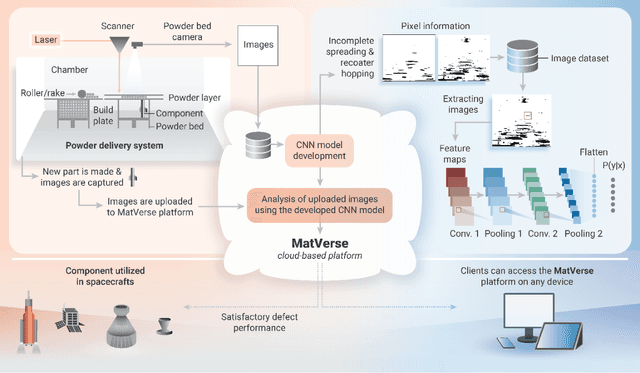
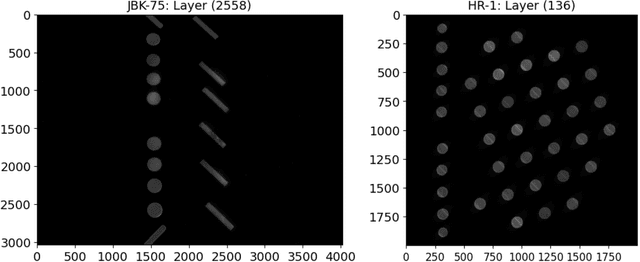
Additive Manufacturing (AM) is transforming the manufacturing sector by enabling efficient production of intricately designed products and small-batch components. However, metal parts produced via AM can include flaws that cause inferior mechanical properties, including reduced fatigue response, yield strength, and fracture toughness. To address this issue, we leverage convolutional neural networks (CNN) to analyze thermal images of printed layers, automatically identifying anomalies that impact these properties. We also investigate various synthetic data generation techniques to address limited and imbalanced AM training data. Our models' defect detection capabilities were assessed using images of Nickel alloy 718 layers produced on a laser powder bed fusion AM machine and synthetic datasets with and without added noise. Our results show significant accuracy improvements with synthetic data, emphasizing the importance of expanding training sets for reliable defect detection. Specifically, Generative Adversarial Networks (GAN)-generated datasets streamlined data preparation by eliminating human intervention while maintaining high performance, thereby enhancing defect detection capabilities. Additionally, our denoising approach effectively improves image quality, ensuring reliable defect detection. Finally, our work integrates these models in the CLoud ADditive MAnufacturing (CLADMA) module, a user-friendly interface, to enhance their accessibility and practicality for AM applications. This integration supports broader adoption and practical implementation of advanced defect detection in AM processes.

Learning in Cooperative Multiagent Systems Using Cognitive and Machine Models

Developing effective Multi-Agent Systems (MAS) is critical for many applications requiring collaboration and coordination with humans. Despite the rapid advance of Multi-Agent Deep Reinforcement Learning (MADRL) in cooperative MAS, one major challenge is the simultaneous learning and interaction of independent agents in dynamic environments in the presence of stochastic rewards. State-of-the-art MADRL models struggle to perform well in Coordinated Multi-agent Object Transportation Problems (CMOTPs), wherein agents must coordinate with each other and learn from stochastic rewards. In contrast, humans often learn rapidly to adapt to nonstationary environments that require coordination among people. In this paper, motivated by the demonstrated ability of cognitive models based on Instance-Based Learning Theory (IBLT) to capture human decisions in many dynamic decision making tasks, we propose three variants of Multi-Agent IBL models (MAIBL). The idea of these MAIBL algorithms is to combine the cognitive mechanisms of IBLT and the techniques of MADRL models to deal with coordination MAS in stochastic environments from the perspective of independent learners. We demonstrate that the MAIBL models exhibit faster learning and achieve better coordination in a dynamic CMOTP task with various settings of stochastic rewards compared to current MADRL models. We discuss the benefits of integrating cognitive insights into MADRL models.

SpeedyIBL: A Solution to the Curse of Exponential Growth in Instance-Based Learning Models of Decisions from Experience

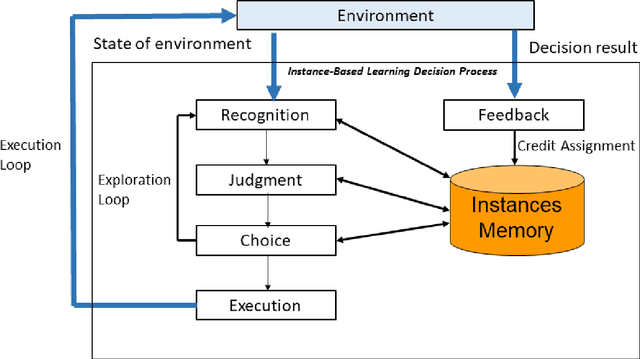
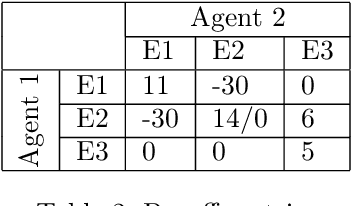
Computational cognitive modeling is a useful methodology to explore and validate theories of human cognitive processes. Often cognitive models are used to simulate the process by which humans perform a task or solve a problem and to make predictions about human behavior. Cognitive models based on Instance-Based Learning (IBL) Theory rely on a formal computational algorithm for dynamic decision making and on a memory mechanism from a well-known cognitive architecture, ACT-R. To advance the computational theory of human decision making and to demonstrate the usefulness of cognitive models in diverse domains, we must address a practical computational problem, the curse of exponential growth, that emerges from memory-based tabular computations. When more observations accumulate, there is an exponential growth of the memory of instances that leads directly to an exponential slow down of the computational time. In this paper, we propose a new Speedy IBL implementation that innovates the mathematics of vectorization and parallel computation over the traditional loop-based approach. Through the implementation of IBL models in many decision games of increasing complexity, we demonstrate the applicability of the regular IBL models and the advantages of their Speedy implementation. Decision games vary in their complexity of decision features and in the number of agents involved in the decision process. The results clearly illustrate that Speedy IBL addresses the curse of exponential growth of memory, reducing the computational time significantly, while maintaining the same level of performance than the traditional implementation of IBL models.

Block Alternating Bregman Majorization Minimization with Extrapolation

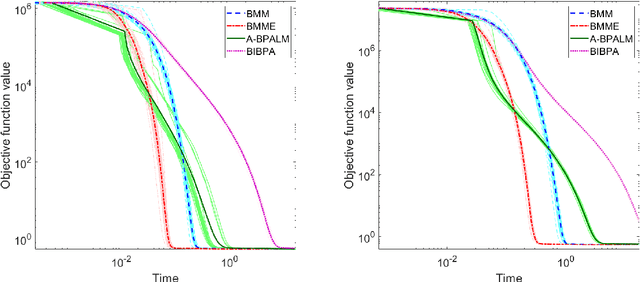
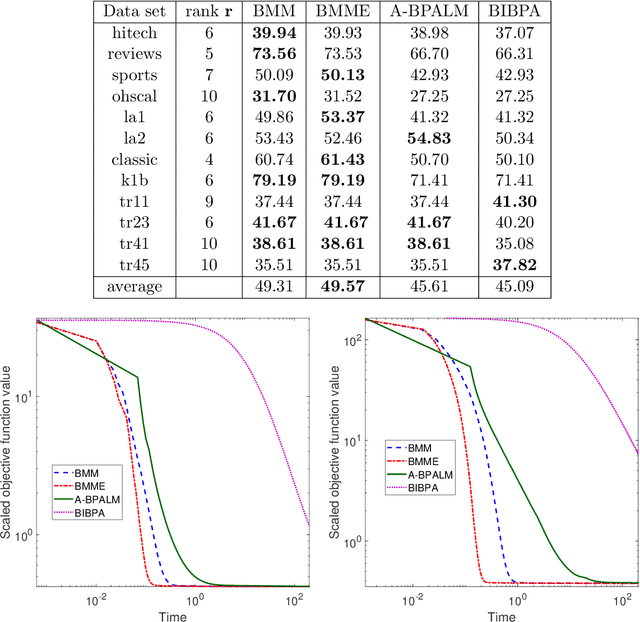
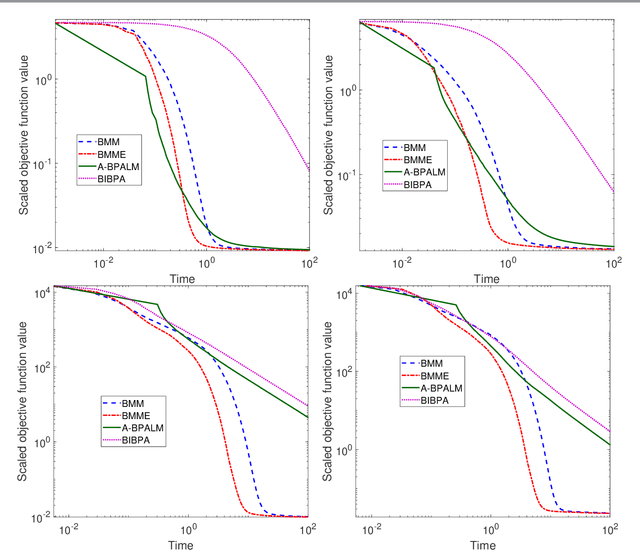
In this paper, we consider a class of nonsmooth nonconvex optimization problems whose objective is the sum of a block relative smooth function and a proper and lower semicontinuous block separable function. Although the analysis of block proximal gradient (BPG) methods for the class of block $L$-smooth functions have been successfully extended to Bregman BPG methods that deal with the class of block relative smooth functions, accelerated Bregman BPG methods are scarce and challenging to design. Taking our inspiration from Nesterov-type acceleration and the majorization-minimization scheme, we propose a block alternating Bregman Majorization-Minimization framework with Extrapolation (BMME). We prove subsequential convergence of BMME to a first-order stationary point under mild assumptions, and study its global convergence under stronger conditions. We illustrate the effectiveness of BMME on the penalized orthogonal nonnegative matrix factorization problem.

A Framework of Inertial Alternating Direction Method of Multipliers for Non-Convex Non-Smooth Optimization

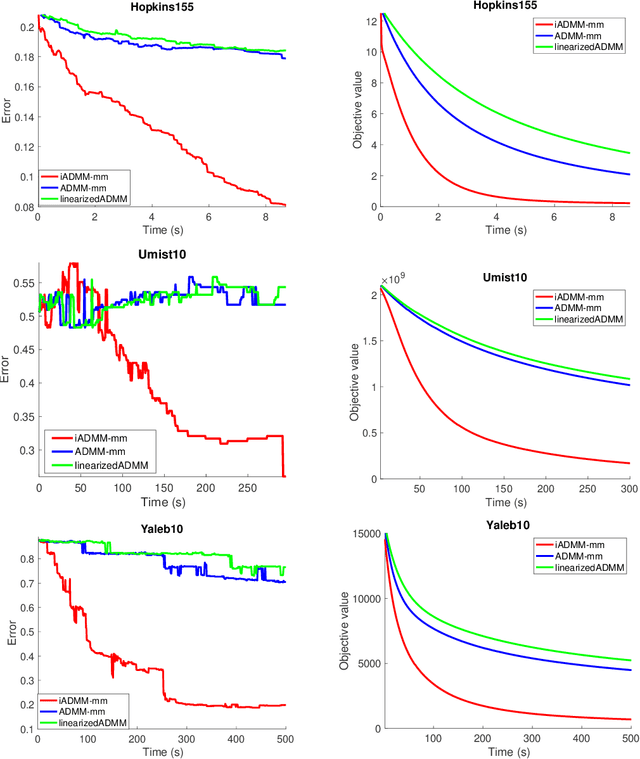
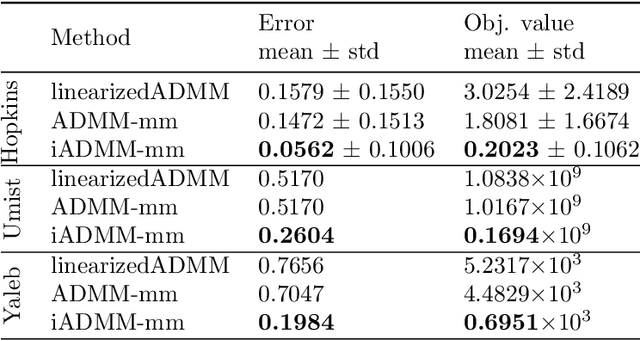
In this paper, we propose an algorithmic framework dubbed inertial alternating direction methods of multipliers (iADMM), for solving a class of nonconvex nonsmooth multiblock composite optimization problems with linear constraints. Our framework employs the general minimization-majorization (MM) principle to update each block of variables so as to not only unify the convergence analysis of previous ADMM that use specific surrogate functions in the MM step, but also lead to new efficient ADMM schemes. To the best of our knowledge, in the \emph{nonconvex nonsmooth} setting, ADMM used in combination with the MM principle to update each block of variables, and ADMM combined with inertial terms for the primal variables have not been studied in the literature. Under standard assumptions, we prove the subsequential convergence and global convergence for the generated sequence of iterates. We illustrate the effectiveness of iADMM on a class of nonconvex low-rank representation problems.

An Inertial Block Majorization Minimization Framework for Nonsmooth Nonconvex Optimization

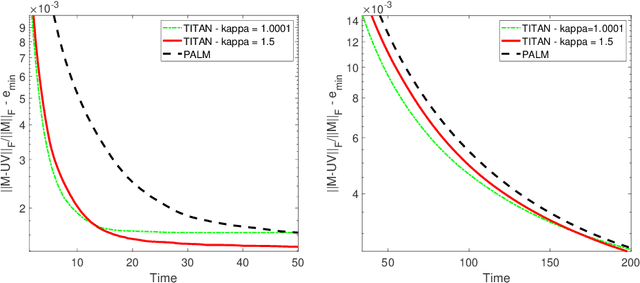
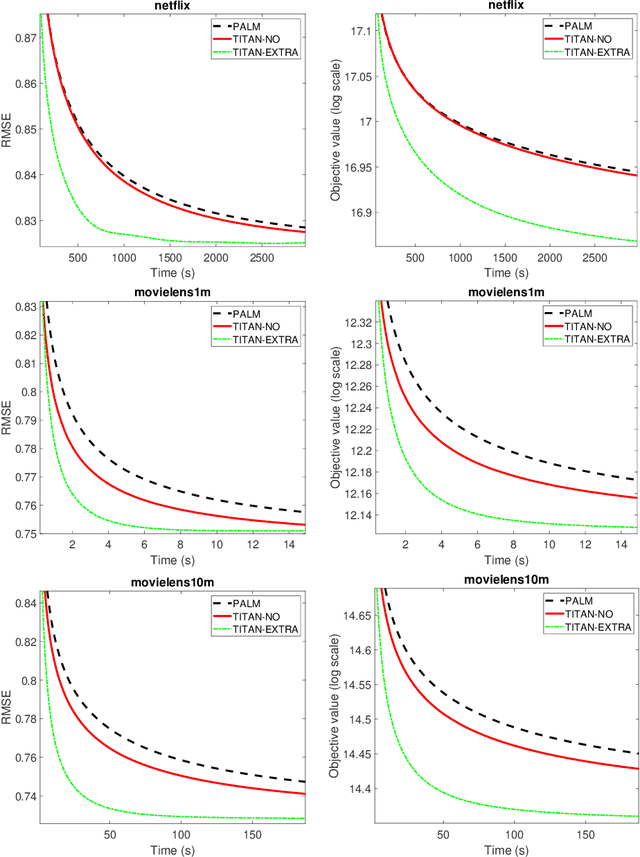
In this paper, we introduce TITAN, a novel inerTial block majorIzation minimization framework for non-smooth non-convex opTimizAtioN problems. TITAN is a block coordinate method (BCM) that embeds inertial force to each majorization-minimization step of the block updates. The inertial force is obtained via an extrapolation operator that subsumes heavy-ball and Nesterov-type accelerations for block proximal gradient methods as special cases. By choosing various surrogate functions, such as proximal, Lipschitz gradient, Bregman, quadratic, and composite surrogate functions, and by varying the extrapolation operator, TITAN produces a rich set of inertial BCMs. We study sub-sequential convergence as well as global convergence for the generated sequence of TITAN. We illustrate the effectiveness of TITAN on two important machine learning problems, namely sparse non-negative matrix factorization and matrix completion.

Stochastic DCA for minimizing a large sum of DC functions with application to Multi-class Logistic Regression

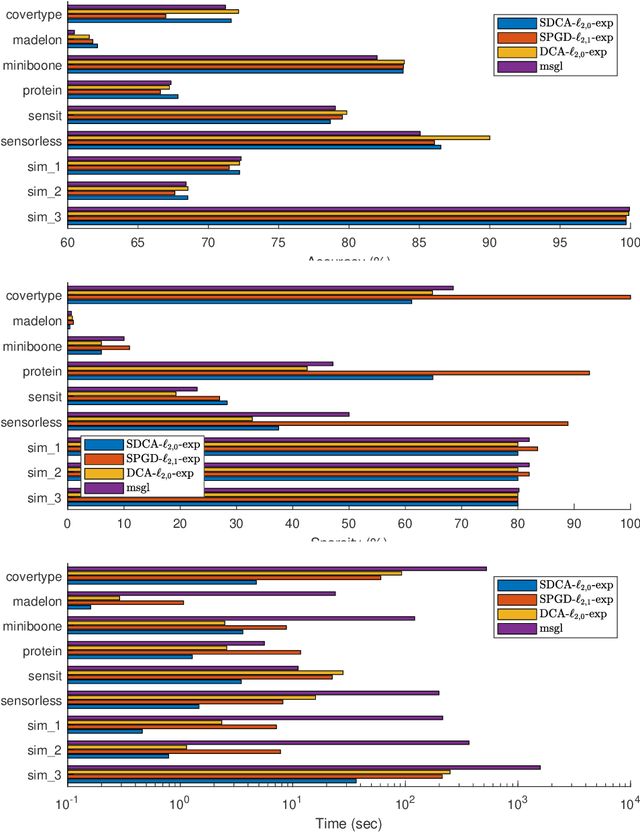
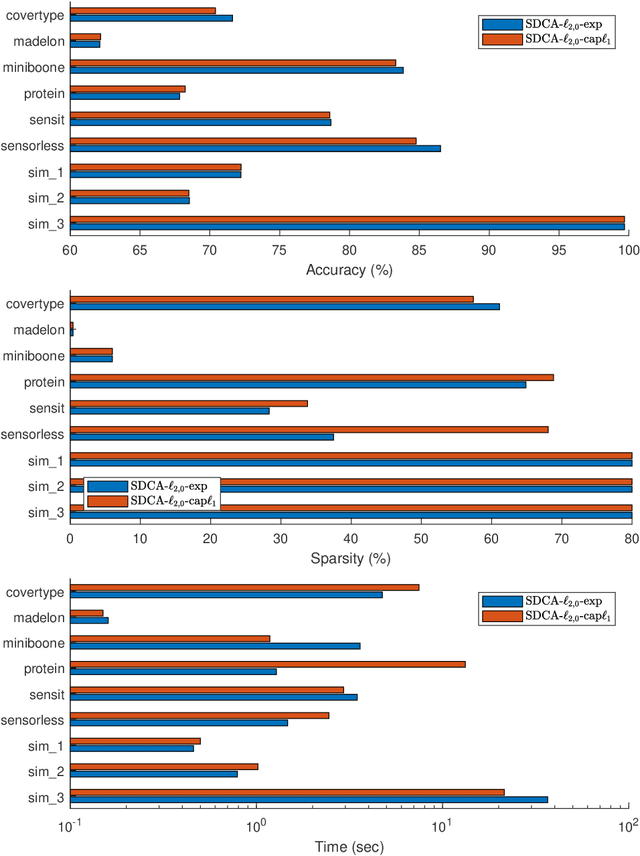
We consider the large sum of DC (Difference of Convex) functions minimization problem which appear in several different areas, especially in stochastic optimization and machine learning. Two DCA (DC Algorithm) based algorithms are proposed: stochastic DCA and inexact stochastic DCA. We prove that the convergence of both algorithms to a critical point is guaranteed with probability one. Furthermore, we develop our stochastic DCA for solving an important problem in multi-task learning, namely group variables selection in multi class logistic regression. The corresponding stochastic DCA is very inexpensive, all computations are explicit. Numerical experiments on several benchmark datasets and synthetic datasets illustrate the efficiency of our algorithms and their superiority over existing methods, with respect to classification accuracy, sparsity of solution as well as running time.

A DCA-Like Algorithm and its Accelerated Version with Application in Data Visualization

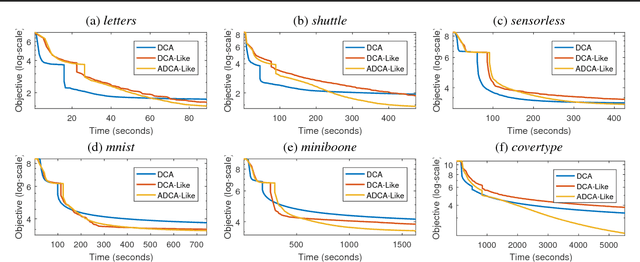
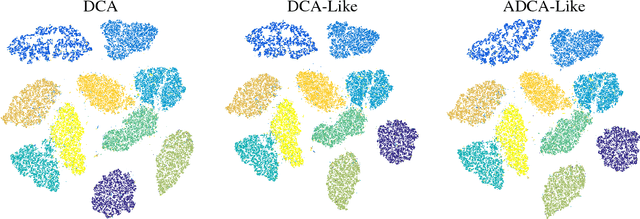
In this paper, we present two variants of DCA (Different of Convex functions Algorithm) to solve the constrained sum of differentiable function and composite functions minimization problem, with the aim of increasing the convergence speed of DCA. In the first variant, DCA-Like, we introduce a new technique to iteratively modify the decomposition of the objective function. This successive decomposition could lead to a better majorization and consequently a better convergence speed than the basic DCA. We then incorporate the Nesterov's acceleration technique into DCA-Like to give rise to the second variant, named Accelerated DCA-Like. The convergence properties and the convergence rate under Kudyka-Lojasiewicz assumption of both variants are rigorously studied. As an application, we investigate our algorithms for the t-distributed stochastic neighbor embedding. Numerical experiments on several benchmark datasets illustrate the efficiency of our algorithms.