A DCA-Like Algorithm and its Accelerated Version with Application in Data Visualization
Paper and Code
Jun 25, 2018
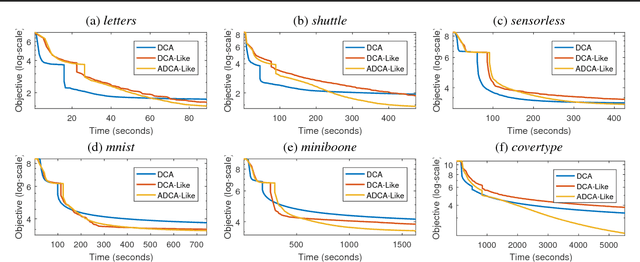
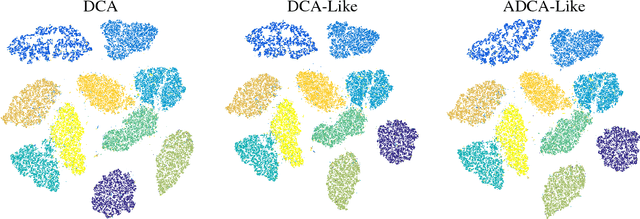
In this paper, we present two variants of DCA (Different of Convex functions Algorithm) to solve the constrained sum of differentiable function and composite functions minimization problem, with the aim of increasing the convergence speed of DCA. In the first variant, DCA-Like, we introduce a new technique to iteratively modify the decomposition of the objective function. This successive decomposition could lead to a better majorization and consequently a better convergence speed than the basic DCA. We then incorporate the Nesterov's acceleration technique into DCA-Like to give rise to the second variant, named Accelerated DCA-Like. The convergence properties and the convergence rate under Kudyka-Lojasiewicz assumption of both variants are rigorously studied. As an application, we investigate our algorithms for the t-distributed stochastic neighbor embedding. Numerical experiments on several benchmark datasets illustrate the efficiency of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge