Hoai An Le Thi
Stochastic DCA for minimizing a large sum of DC functions with application to Multi-class Logistic Regression
Nov 10, 2019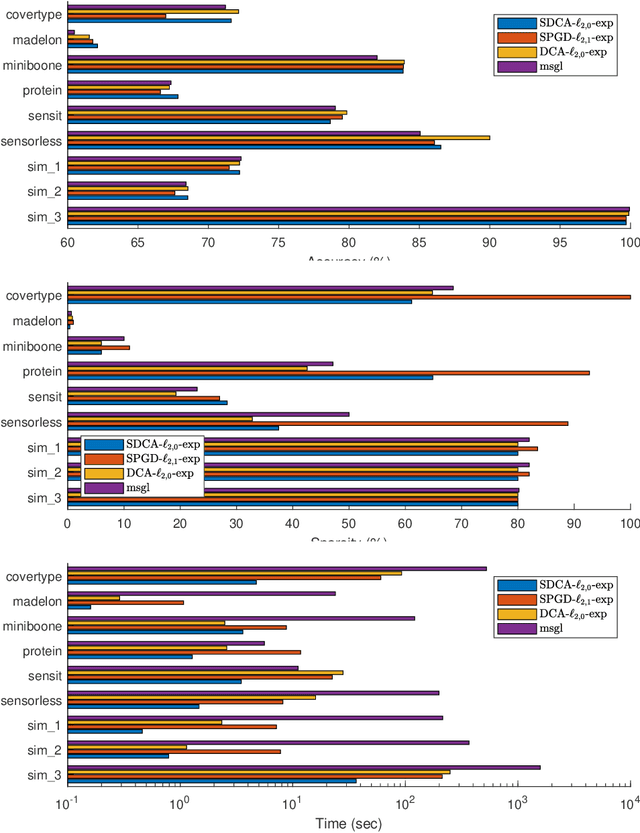


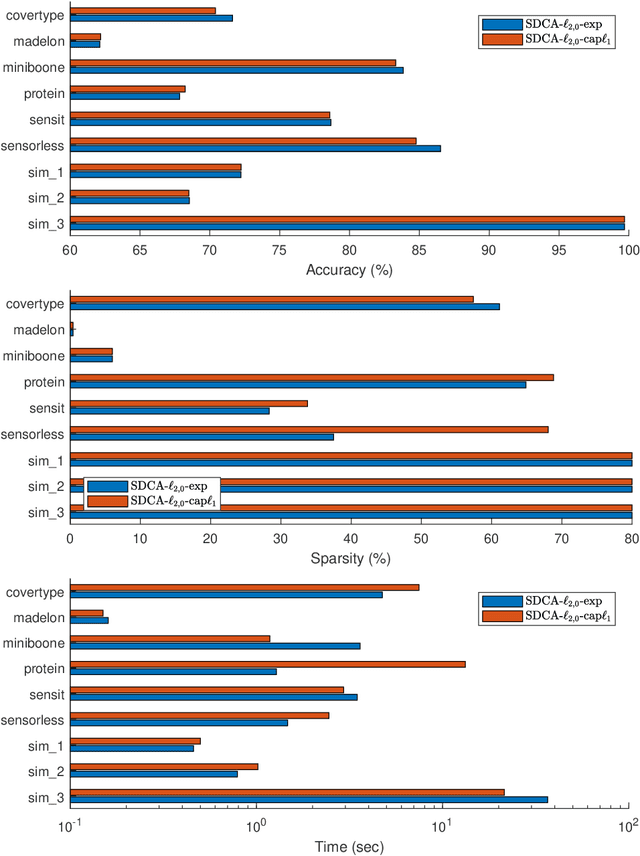
Abstract:We consider the large sum of DC (Difference of Convex) functions minimization problem which appear in several different areas, especially in stochastic optimization and machine learning. Two DCA (DC Algorithm) based algorithms are proposed: stochastic DCA and inexact stochastic DCA. We prove that the convergence of both algorithms to a critical point is guaranteed with probability one. Furthermore, we develop our stochastic DCA for solving an important problem in multi-task learning, namely group variables selection in multi class logistic regression. The corresponding stochastic DCA is very inexpensive, all computations are explicit. Numerical experiments on several benchmark datasets and synthetic datasets illustrate the efficiency of our algorithms and their superiority over existing methods, with respect to classification accuracy, sparsity of solution as well as running time.
A DCA-Like Algorithm and its Accelerated Version with Application in Data Visualization
Jun 25, 2018
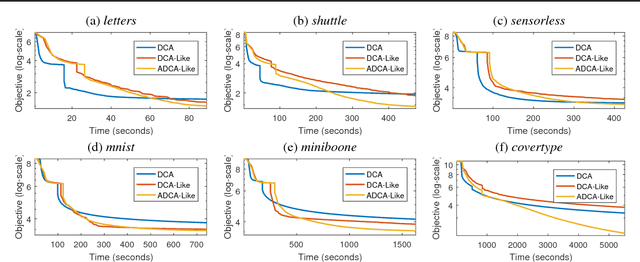
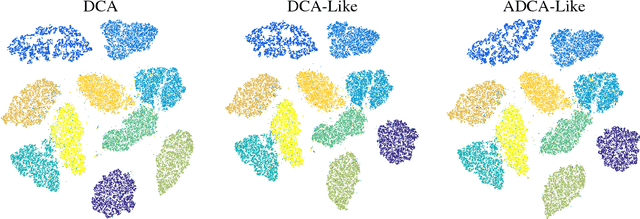
Abstract:In this paper, we present two variants of DCA (Different of Convex functions Algorithm) to solve the constrained sum of differentiable function and composite functions minimization problem, with the aim of increasing the convergence speed of DCA. In the first variant, DCA-Like, we introduce a new technique to iteratively modify the decomposition of the objective function. This successive decomposition could lead to a better majorization and consequently a better convergence speed than the basic DCA. We then incorporate the Nesterov's acceleration technique into DCA-Like to give rise to the second variant, named Accelerated DCA-Like. The convergence properties and the convergence rate under Kudyka-Lojasiewicz assumption of both variants are rigorously studied. As an application, we investigate our algorithms for the t-distributed stochastic neighbor embedding. Numerical experiments on several benchmark datasets illustrate the efficiency of our algorithms.
DC approximation approaches for sparse optimization
Jul 02, 2014



Abstract:Sparse optimization refers to an optimization problem involving the zero-norm in objective or constraints. In this paper, nonconvex approximation approaches for sparse optimization have been studied with a unifying point of view in DC (Difference of Convex functions) programming framework. Considering a common DC approximation of the zero-norm including all standard sparse inducing penalty functions, we studied the consistency between global minimums (resp. local minimums) of approximate and original problems. We showed that, in several cases, some global minimizers (resp. local minimizers) of the approximate problem are also those of the original problem. Using exact penalty techniques in DC programming, we proved stronger results for some particular approximations, namely, the approximate problem, with suitable parameters, is equivalent to the original problem. The efficiency of several sparse inducing penalty functions have been fully analyzed. Four DCA (DC Algorithm) schemes were developed that cover all standard algorithms in nonconvex sparse approximation approaches as special versions. They can be viewed as, an $\ell _{1}$-perturbed algorithm / reweighted-$\ell _{1}$ algorithm / reweighted-$\ell _{1}$ algorithm. We offer a unifying nonconvex approximation approach, with solid theoretical tools as well as efficient algorithms based on DC programming and DCA, to tackle the zero-norm and sparse optimization. As an application, we implemented our methods for the feature selection in SVM (Support Vector Machine) problem and performed empirical comparative numerical experiments on the proposed algorithms with various approximation functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge