Self-Supervised Learning with Multi-View Rendering for 3D Point Cloud Analysis

Recently, great progress has been made in 3D deep learning with the emergence of deep neural networks specifically designed for 3D point clouds. These networks are often trained from scratch or from pre-trained models learned purely from point cloud data. Inspired by the success of deep learning in the image domain, we devise a novel pre-training technique for better model initialization by utilizing the multi-view rendering of the 3D data. Our pre-training is self-supervised by a local pixel/point level correspondence loss computed from perspective projection and a global image/point cloud level loss based on knowledge distillation, thus effectively improving upon popular point cloud networks, including PointNet, DGCNN and SR-UNet. These improved models outperform existing state-of-the-art methods on various datasets and downstream tasks. We also analyze the benefits of synthetic and real data for pre-training, and observe that pre-training on synthetic data is also useful for high-level downstream tasks. Code and pre-trained models are available at https://github.com/VinAIResearch/selfsup_pcd.

Bag of biterms modeling for short texts

Analyzing texts from social media encounters many challenges due to their unique characteristics of shortness, massiveness, and dynamic. Short texts do not provide enough context information, causing the failure of the traditional statistical models. Furthermore, many applications often face with massive and dynamic short texts, causing various computational challenges to the current batch learning algorithms. This paper presents a novel framework, namely Bag of Biterms Modeling (BBM), for modeling massive, dynamic, and short text collections. BBM comprises of two main ingredients: (1) the concept of Bag of Biterms (BoB) for representing documents, and (2) a simple way to help statistical models to include BoB. Our framework can be easily deployed for a large class of probabilistic models, and we demonstrate its usefulness with two well-known models: Latent Dirichlet Allocation (LDA) and Hierarchical Dirichlet Process (HDP). By exploiting both terms (words) and biterms (pairs of words), the major advantages of BBM are: (1) it enhances the length of the documents and makes the context more coherent by emphasizing the word connotation and co-occurrence via Bag of Biterms, (2) it inherits inference and learning algorithms from the primitive to make it straightforward to design online and streaming algorithms for short texts. Extensive experiments suggest that BBM outperforms several state-of-the-art models. We also point out that the BoB representation performs better than the traditional representations (e.g, Bag of Words, tf-idf) even for normal texts.

Stochastic DCA for minimizing a large sum of DC functions with application to Multi-class Logistic Regression

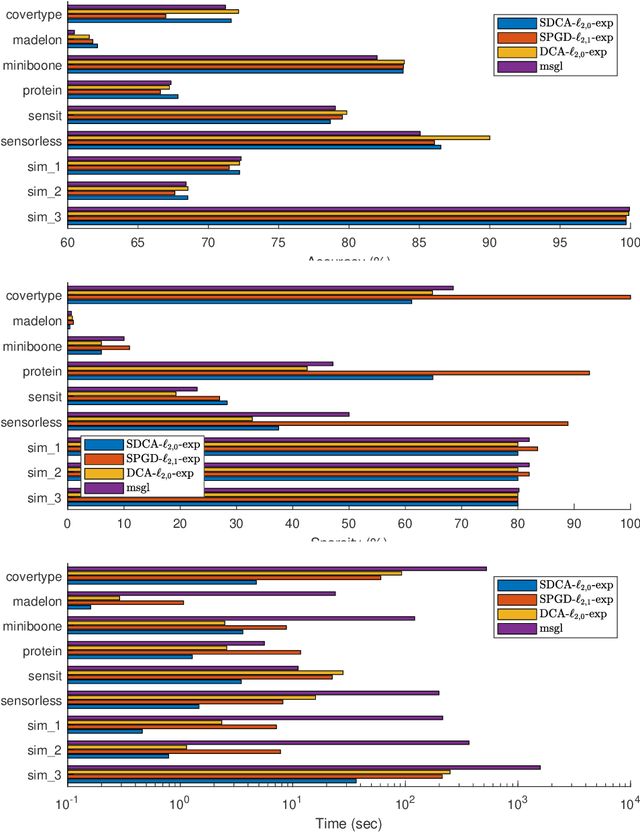
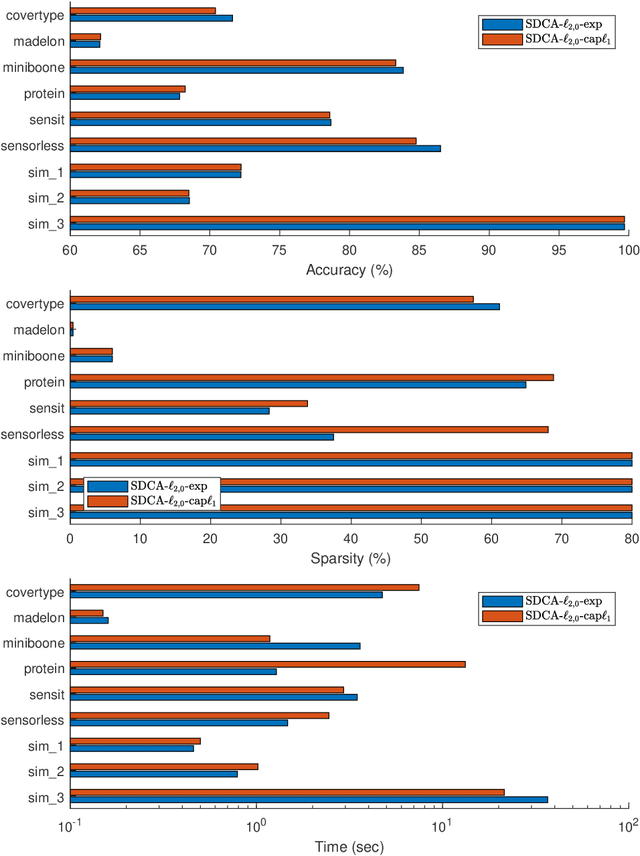
We consider the large sum of DC (Difference of Convex) functions minimization problem which appear in several different areas, especially in stochastic optimization and machine learning. Two DCA (DC Algorithm) based algorithms are proposed: stochastic DCA and inexact stochastic DCA. We prove that the convergence of both algorithms to a critical point is guaranteed with probability one. Furthermore, we develop our stochastic DCA for solving an important problem in multi-task learning, namely group variables selection in multi class logistic regression. The corresponding stochastic DCA is very inexpensive, all computations are explicit. Numerical experiments on several benchmark datasets and synthetic datasets illustrate the efficiency of our algorithms and their superiority over existing methods, with respect to classification accuracy, sparsity of solution as well as running time.

A DCA-Like Algorithm and its Accelerated Version with Application in Data Visualization

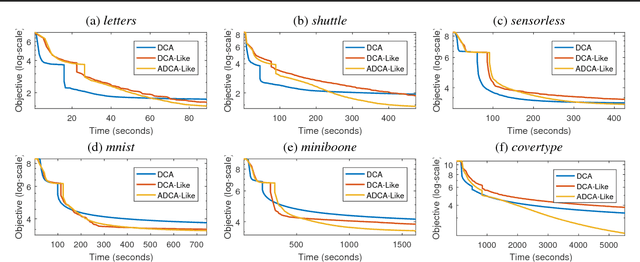
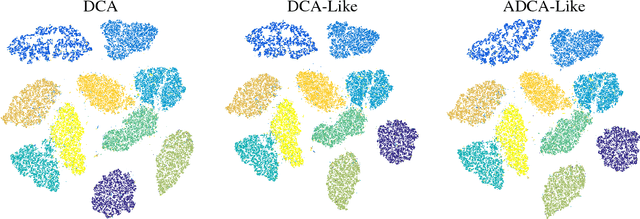
In this paper, we present two variants of DCA (Different of Convex functions Algorithm) to solve the constrained sum of differentiable function and composite functions minimization problem, with the aim of increasing the convergence speed of DCA. In the first variant, DCA-Like, we introduce a new technique to iteratively modify the decomposition of the objective function. This successive decomposition could lead to a better majorization and consequently a better convergence speed than the basic DCA. We then incorporate the Nesterov's acceleration technique into DCA-Like to give rise to the second variant, named Accelerated DCA-Like. The convergence properties and the convergence rate under Kudyka-Lojasiewicz assumption of both variants are rigorously studied. As an application, we investigate our algorithms for the t-distributed stochastic neighbor embedding. Numerical experiments on several benchmark datasets illustrate the efficiency of our algorithms.