Imitation Learning from Observations: An Autoregressive Mixture of Experts Approach

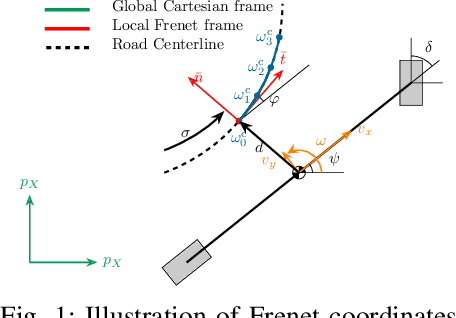
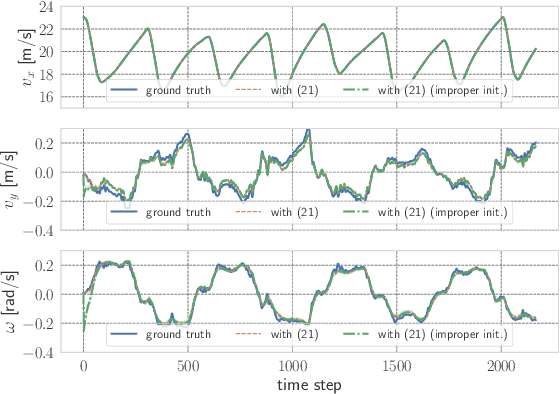
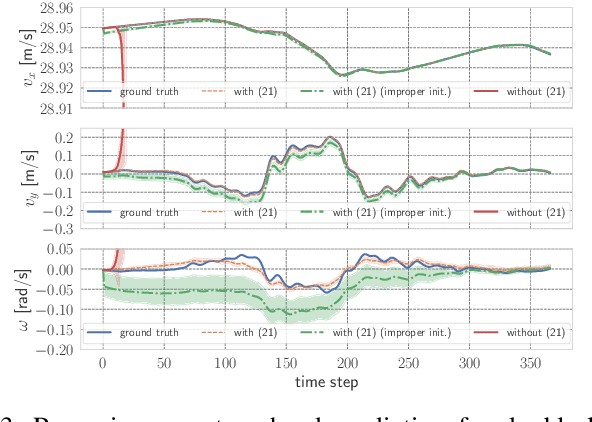
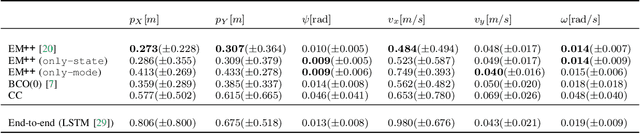
This paper presents a novel approach to imitation learning from observations, where an autoregressive mixture of experts model is deployed to fit the underlying policy. The parameters of the model are learned via a two-stage framework. By leveraging the existing dynamics knowledge, the first stage of the framework estimates the control input sequences and hence reduces the problem complexity. At the second stage, the policy is learned by solving a regularized maximum-likelihood estimation problem using the estimated control input sequences. We further extend the learning procedure by incorporating a Lyapunov stability constraint to ensure asymptotic stability of the identified model, for accurate multi-step predictions. The effectiveness of the proposed framework is validated using two autonomous driving datasets collected from human demonstrations, demonstrating its practical applicability in modelling complex nonlinear dynamics.

The inexact power augmented Lagrangian method for constrained nonconvex optimization

This work introduces an unconventional inexact augmented Lagrangian method, where the augmenting term is a Euclidean norm raised to a power between one and two. The proposed algorithm is applicable to a broad class of constrained nonconvex minimization problems, that involve nonlinear equality constraints over a convex set under a mild regularity condition. First, we conduct a full complexity analysis of the method, leveraging an accelerated first-order algorithm for solving the H\"older-smooth subproblems. Next, we present an inexact proximal point method to tackle these subproblems, demonstrating that it achieves an improved convergence rate. Notably, this rate reduces to the best-known convergence rate for first-order methods when the augmenting term is a squared Euclidean norm. Our worst-case complexity results further show that using lower powers for the augmenting term leads to faster constraint satisfaction, albeit with a slower decrease in the dual residual. Numerical experiments support our theoretical findings, illustrating that this trade-off between constraint satisfaction and cost minimization is advantageous for certain practical problems.

Stability of Primal-Dual Gradient Flow Dynamics for Multi-Block Convex Optimization Problems

We examine stability properties of primal-dual gradient flow dynamics for composite convex optimization problems with multiple, possibly nonsmooth, terms in the objective function under the generalized consensus constraint. The proposed dynamics are based on the proximal augmented Lagrangian and they provide a viable alternative to ADMM which faces significant challenges from both analysis and implementation viewpoints in large-scale multi-block scenarios. In contrast to customized algorithms with individualized convergence guarantees, we provide a systematic approach for solving a broad class of challenging composite optimization problems. We leverage various structural properties to establish global (exponential) convergence guarantees for the proposed dynamics. Our assumptions are much weaker than those required to prove (exponential) stability of various primal-dual dynamics as well as (linear) convergence of discrete-time methods, e.g., standard two-block and multi-block ADMM and EXTRA algorithms. Finally, we show necessity of some of our structural assumptions for exponential stability and provide computational experiments to demonstrate the convenience of the proposed dynamics for parallel and distributed computing applications.

Quantization-free Lossy Image Compression Using Integer Matrix Factorization

Lossy image compression is essential for efficient transmission and storage. Traditional compression methods mainly rely on discrete cosine transform (DCT) or singular value decomposition (SVD), both of which represent image data in continuous domains and therefore necessitate carefully designed quantizers. Notably, SVD-based methods are more sensitive to quantization errors than DCT-based methods like JPEG. To address this issue, we introduce a variant of integer matrix factorization (IMF) to develop a novel quantization-free lossy image compression method. IMF provides a low-rank representation of the image data as a product of two smaller factor matrices with bounded integer elements, thereby eliminating the need for quantization. We propose an efficient, provably convergent iterative algorithm for IMF using a block coordinate descent (BCD) scheme, with subproblems having closed-form solutions. Our experiments on the Kodak and CLIC 2024 datasets demonstrate that our IMF compression method consistently outperforms JPEG at low bit rates below 0.25 bits per pixel (bpp) and remains comparable at higher bit rates. We also assessed our method's capability to preserve visual semantics by evaluating an ImageNet pre-trained classifier on compressed images. Remarkably, our method improved top-1 accuracy by over 5 percentage points compared to JPEG at bit rates under 0.25 bpp. The project is available at https://github.com/pashtari/lrf .

Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

Learning Based NMPC Adaptation for Autonomous Driving using Parallelized Digital Twin

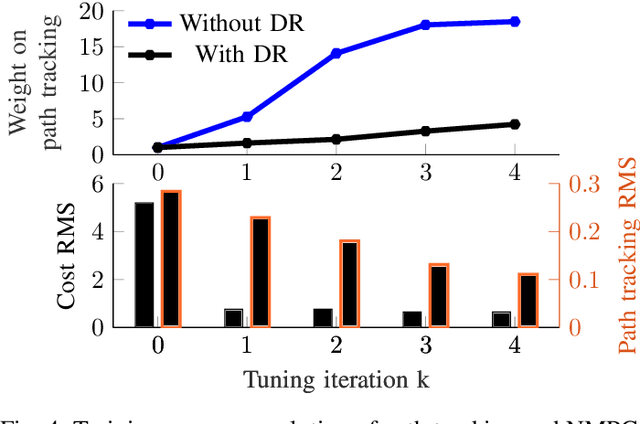
In this work, we address the problem of transferring an autonomous driving (AD) module from one domain to another, in particular from simulation to the real world (Sim2Real). We propose a data-efficient method for online and on-the-fly learning based adaptation for parametrizable control architectures such that the target closed-loop performance is optimized under several uncertainty sources such as model mismatches, environment changes and task choice. The novelty of the work resides in leveraging black-box optimization enabled by executable digital twins, with data-driven hyper-parameter tuning through derivative-free methods to directly adapt in real-time the AD module. Our proposed method requires a minimal amount of interaction with the real-world in the randomization and online training phase. Specifically, we validate our approach in real-world experiments and show the ability to transfer and safely tune a nonlinear model predictive controller in less than 10 minutes, eliminating the need of day-long manual tuning and hours-long machine learning training phases. Our results show that the online adapted NMPC directly compensates for disturbances, avoids overtuning in simulation and for one specific task, and it generalizes for less than 15cm of tracking accuracy over a multitude of trajectories, and leads to 83% tracking improvement.

Adaptive proximal gradient methods are universal without approximation

We show that adaptive proximal gradient methods for convex problems are not restricted to traditional Lipschitzian assumptions. Our analysis reveals that a class of linesearch-free methods is still convergent under mere local H\"older gradient continuity, covering in particular continuously differentiable semi-algebraic functions. To mitigate the lack of local Lipschitz continuity, popular approaches revolve around $\varepsilon$-oracles and/or linesearch procedures. In contrast, we exploit plain H\"older inequalities not entailing any approximation, all while retaining the linesearch-free nature of adaptive schemes. Furthermore, we prove full sequence convergence without prior knowledge of local H\"older constants nor of the order of H\"older continuity. In numerical experiments we present comparisons to baseline methods on diverse tasks from machine learning covering both the locally and the globally H\"older setting.

Convergence of the Chambolle-Pock Algorithm in the Absence of Monotonicity

The Chambolle-Pock algorithm (CPA), also known as the primal-dual hybrid gradient method (PDHG), has surged in popularity in the last decade due to its success in solving convex/monotone structured problems. This work provides convergence results for problems with varying degrees of (non)monotonicity, quantified through a so-called oblique weak Minty condition on the associated primal-dual operator. Our results reveal novel stepsize and relaxation parameter ranges which do not only depend on the norm of the linear mapping, but also on its other singular values. In particular, in nonmonotone settings, in addition to the classical stepsize conditions for CPA, extra bounds on the stepsizes and relaxation parameters are required. On the other hand, in the strongly monotone setting, the relaxation parameter is allowed to exceed the classical upper bound of two. Moreover, sufficient convergence conditions are obtained when the individual operators belong to the recently introduced class of semimonotone operators. Since this class of operators encompasses many traditional operator classes including (hypo)- and co(hypo)monotone operators, this analysis recovers and extends existing results for CPA. Several examples are provided for the aforementioned problem classes to demonstrate and establish tightness of the proposed stepsize ranges.

On the convergence of adaptive first order methods: proximal gradient and alternating minimization algorithms

Building upon recent works on linesearch-free adaptive proximal gradient methods, this paper proposes AdaPG$^{\pi,r}$, a framework that unifies and extends existing results by providing larger stepsize policies and improved lower bounds. Different choices of the parameters $\pi$ and $r$ are discussed and the efficacy of the resulting methods is demonstrated through numerical simulations. In an attempt to better understand the underlying theory, its convergence is established in a more general setting that allows for time-varying parameters. Finally, an adaptive alternating minimization algorithm is presented by exploring the dual setting. This algorithm not only incorporates additional adaptivity, but also expands its applicability beyond standard strongly convex settings.

A Deep Learning Based Resource Allocator for Communication Systems with Dynamic User Utility Demands

Deep learning (DL) based resource allocation (RA) has recently gained a lot of attention due to its performance efficiency. However, most of the related studies assume an ideal case where the number of users and their utility demands, e.g., data rate constraints, are fixed and the designed DL based RA scheme exploits a policy trained only for these fixed parameters. A computationally complex policy retraining is required whenever these parameters change. Therefore, in this paper, a DL based resource allocator (ALCOR) is introduced, which allows users to freely adjust their utility demands based on, e.g., their application layer. ALCOR employs deep neural networks (DNNs), as the policy, in an iterative optimization algorithm. The optimization algorithm aims to optimize the on-off status of users in a time-sharing problem to satisfy their utility demands in expectation. The policy performs unconstrained RA (URA) -- RA without taking into account user utility demands -- among active users to maximize the sum utility (SU) at each time instant. Based on the chosen URA scheme, ALCOR can perform RA in a model-based or model-free manner and in a centralized or distributed scenario. Derived convergence analyses provide guarantees for the convergence of ALCOR, and numerical experiments corroborate its effectiveness.