Chameleon: A Flexible Data-mixing Framework for Language Model Pretraining and Finetuning

Training data mixtures greatly impact the generalization performance of large language models. Existing domain reweighting methods often rely on costly weight computations and require retraining when new data is introduced. To this end, we introduce a flexible and efficient data mixing framework, Chameleon, that employs leverage scores to quantify domain importance within a learned embedding space. We first construct a domain affinity matrix over domain embeddings. The induced leverage scores determine a mixture that upweights domains sharing common representations in embedding space. This formulation allows direct transfer to new data by computing the new domain embeddings. In experiments, we demonstrate improvements over three key scenarios: (i) our computed weights improve performance on pretraining domains with a fraction of the compute of existing methods; (ii) Chameleon can adapt to data changes without proxy retraining, boosting few-shot reasoning accuracies when transferred to new data; (iii) our method enables efficient domain reweighting in finetuning, consistently improving test perplexity on all finetuning domains over uniform mixture. Our code is available at https://github.com/LIONS-EPFL/Chameleon.

Efficient Large Language Model Inference with Neural Block Linearization

The high inference demands of transformer-based Large Language Models (LLMs) pose substantial challenges in their deployment. To this end, we introduce Neural Block Linearization (NBL), a novel framework for accelerating transformer model inference by replacing self-attention layers with linear approximations derived from Linear Minimum Mean Squared Error estimators. NBL leverages Canonical Correlation Analysis to compute a theoretical upper bound on the approximation error. Then, we use this bound as a criterion for substitution, selecting the LLM layers with the lowest linearization error. NBL can be efficiently applied to pre-trained LLMs without the need for fine-tuning. In experiments, NBL achieves notable computational speed-ups while preserving competitive accuracy on multiple reasoning benchmarks. For instance, applying NBL to 12 self-attention layers in DeepSeek-R1-Distill-Llama-8B increases the inference speed by 32% with less than 1% accuracy trade-off, making it a flexible and promising solution to improve the inference efficiency of LLMs.

Quantum-PEFT: Ultra parameter-efficient fine-tuning

This paper introduces Quantum-PEFT that leverages quantum computations for parameter-efficient fine-tuning (PEFT). Unlike other additive PEFT methods, such as low-rank adaptation (LoRA), Quantum-PEFT exploits an underlying full-rank yet surprisingly parameter efficient quantum unitary parameterization. With the use of Pauli parameterization, the number of trainable parameters grows only logarithmically with the ambient dimension, as opposed to linearly as in LoRA-based PEFT methods. Quantum-PEFT achieves vanishingly smaller number of trainable parameters than the lowest-rank LoRA as dimensions grow, enhancing parameter efficiency while maintaining a competitive performance. We apply Quantum-PEFT to several transfer learning benchmarks in language and vision, demonstrating significant advantages in parameter efficiency.

Linear Attention for Efficient Bidirectional Sequence Modeling

Transformers with linear attention enable fast and parallel training. Moreover, they can be formulated as Recurrent Neural Networks (RNNs), for efficient linear-time inference. While extensively evaluated in causal sequence modeling, they have yet to be extended to the bidirectional setting. This work introduces the LION framework, establishing new theoretical foundations for linear transformers in bidirectional sequence modeling. LION constructs a bidirectional RNN equivalent to full Linear Attention. This extends the benefits of linear transformers: parallel training, and efficient inference, into the bidirectional setting. Using LION, we cast three linear transformers to their bidirectional form: LION-LIT, the bidirectional variant corresponding to (Katharopoulos et al., 2020); LION-D, extending RetNet (Sun et al., 2023); and LION-S, a linear transformer with a stable selective mask inspired by selectivity of SSMs (Dao & Gu, 2024). Replacing the attention block with LION (-LIT, -D, -S) achieves performance on bidirectional tasks that approaches that of Transformers and State-Space Models (SSMs), while delivering significant improvements in training speed. Our implementation is available in http://github.com/LIONS-EPFL/LION.

Membership Inference Attacks against Large Vision-Language Models

Large vision-language models (VLLMs) exhibit promising capabilities for processing multi-modal tasks across various application scenarios. However, their emergence also raises significant data security concerns, given the potential inclusion of sensitive information, such as private photos and medical records, in their training datasets. Detecting inappropriately used data in VLLMs remains a critical and unresolved issue, mainly due to the lack of standardized datasets and suitable methodologies. In this study, we introduce the first membership inference attack (MIA) benchmark tailored for various VLLMs to facilitate training data detection. Then, we propose a novel MIA pipeline specifically designed for token-level image detection. Lastly, we present a new metric called MaxR\'enyi-K%, which is based on the confidence of the model output and applies to both text and image data. We believe that our work can deepen the understanding and methodology of MIAs in the context of VLLMs. Our code and datasets are available at https://github.com/LIONS-EPFL/VL-MIA.

Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

HeNCler: Node Clustering in Heterophilous Graphs through Learned Asymmetric Similarity

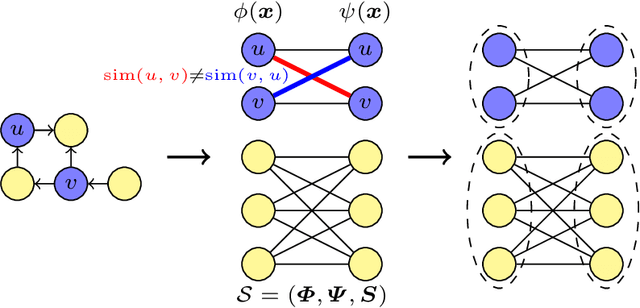
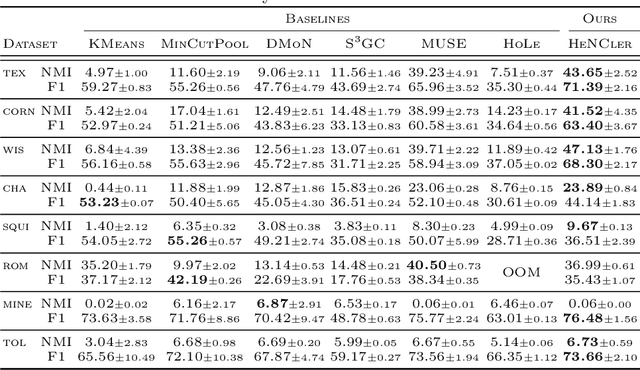
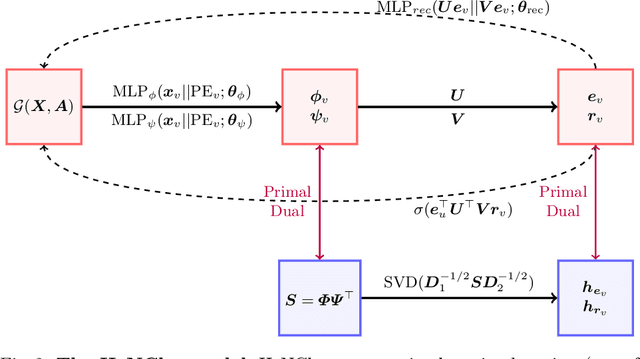
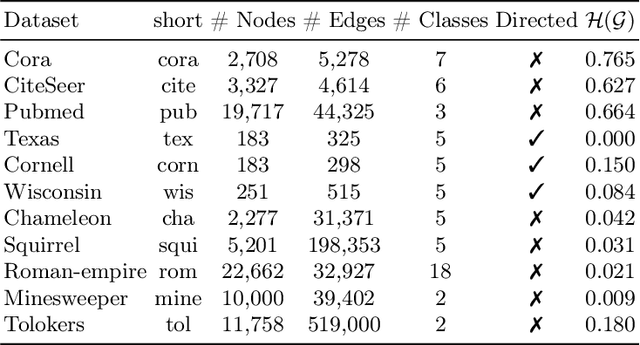
Clustering nodes in heterophilous graphs presents unique challenges due to the asymmetric relationships often overlooked by traditional methods, which moreover assume that good clustering corresponds to high intra-cluster and low inter-cluster connectivity. To address these issues, we introduce HeNCler - a novel approach for Heterophilous Node Clustering. Our method begins by defining a weighted kernel singular value decomposition to create an asymmetric similarity graph, applicable to both directed and undirected graphs. We further establish that the dual problem of this formulation aligns with asymmetric kernel spectral clustering, interpreting learned graph similarities without relying on homophily. We demonstrate the ability to solve the primal problem directly, circumventing the computational difficulties of the dual approach. Experimental evidence confirms that HeNCler significantly enhances performance in node clustering tasks within heterophilous graph contexts.

Self-Attention through Kernel-Eigen Pair Sparse Variational Gaussian Processes

While the great capability of Transformers significantly boosts prediction accuracy, it could also yield overconfident predictions and require calibrated uncertainty estimation, which can be commonly tackled by Gaussian processes (GPs). Existing works apply GPs with symmetric kernels under variational inference to the attention kernel; however, omitting the fact that attention kernels are in essence asymmetric. Moreover, the complexity of deriving the GP posteriors remains high for large-scale data. In this work, we propose Kernel-Eigen Pair Sparse Variational Gaussian Processes (KEP-SVGP) for building uncertainty-aware self-attention where the asymmetry of attention kernels is tackled by Kernel SVD (KSVD) and a reduced complexity is acquired. Through KEP-SVGP, i) the SVGP pair induced by the two sets of singular vectors from KSVD w.r.t. the attention kernel fully characterizes the asymmetry; ii) using only a small set of adjoint eigenfunctions from KSVD, the derivation of SVGP posteriors can be based on the inversion of a diagonal matrix containing singular values, contributing to a reduction in time complexity; iii) an evidence lower bound is derived so that variational parameters can be optimized towards this objective. Experiments verify our excellent performances and efficiency on in-distribution, distribution-shift and out-of-distribution benchmarks.

Combining Primal and Dual Representations in Deep Restricted Kernel Machines Classifiers

In contrast to deep networks, kernel methods cannot directly take advantage of depth. In this regard, the deep Restricted Kernel Machine (DRKM) framework allows multiple levels of kernel PCA (KPCA) and Least-Squares Support Vector Machines (LSSVM) to be combined into a deep architecture using visible and hidden units. We propose a new method for DRKM classification coupling the objectives of KPCA and classification levels, with the hidden feature matrix lying on the Stiefel manifold. The classification level can be formulated as an LSSVM or as an MLP feature map, combining depth in terms of levels and layers. The classification level is expressed in its primal formulation, as the deep KPCA levels can embed the most informative components of the data in a much lower dimensional space. In the experiments on benchmark datasets with few available training points, we show that our deep method improves over the LSSVM/MLP and that models with multiple KPCA levels can outperform models with a single level.

Nonlinear SVD with Asymmetric Kernels: feature learning and asymmetric Nyström method

Asymmetric data naturally exist in real life, such as directed graphs. Different from the common kernel methods requiring Mercer kernels, this paper tackles the asymmetric kernel-based learning problem. We describe a nonlinear extension of the matrix Singular Value Decomposition through asymmetric kernels, namely KSVD. First, we construct two nonlinear feature mappings w.r.t. rows and columns of the given data matrix. The proposed optimization problem maximizes the variance of each mapping projected onto the subspace spanned by the other, subject to a mutual orthogonality constraint. Through Lagrangian duality, we show that it can be solved by the left and right singular vectors in the feature space induced by the asymmetric kernel. Moreover, we start from the integral equations with a pair of adjoint eigenfunctions corresponding to the singular vectors on an asymmetrical kernel, and extend the Nystr\"om method to asymmetric cases through the finite sample approximation, which can be applied to speedup the training in KSVD. Experiments show that asymmetric KSVD learns features outperforming Mercer-kernel based methods that resort to symmetrization, and also verify the effectiveness of the asymmetric Nystr\"om method.