Sonny Achten
Generative Kernel Spectral Clustering
Feb 04, 2025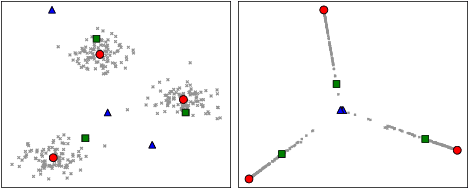
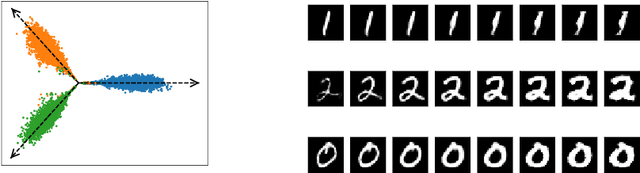

Abstract:Modern clustering approaches often trade interpretability for performance, particularly in deep learning-based methods. We present Generative Kernel Spectral Clustering (GenKSC), a novel model combining kernel spectral clustering with generative modeling to produce both well-defined clusters and interpretable representations. By augmenting weighted variance maximization with reconstruction and clustering losses, our model creates an explorable latent space where cluster characteristics can be visualized through traversals along cluster directions. Results on MNIST and FashionMNIST datasets demonstrate the model's ability to learn meaningful cluster representations.
HeNCler: Node Clustering in Heterophilous Graphs through Learned Asymmetric Similarity
May 27, 2024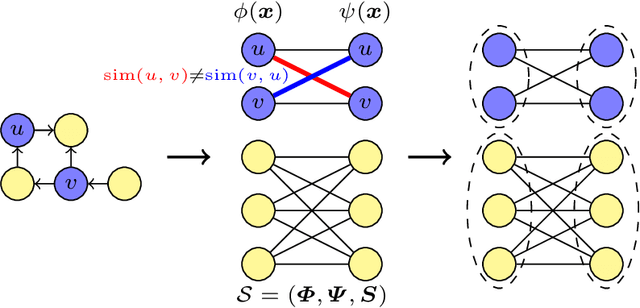
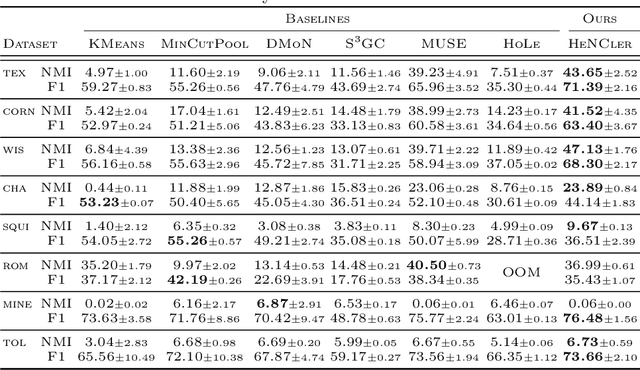
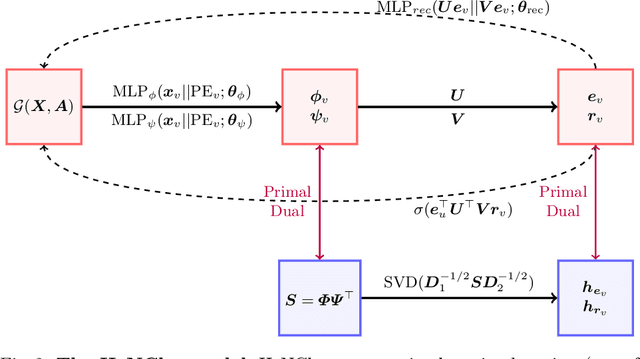
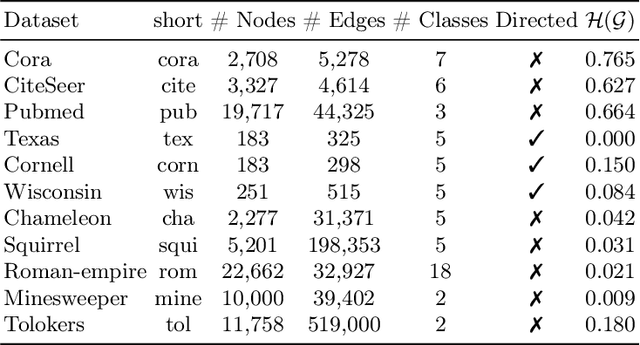
Abstract:Clustering nodes in heterophilous graphs presents unique challenges due to the asymmetric relationships often overlooked by traditional methods, which moreover assume that good clustering corresponds to high intra-cluster and low inter-cluster connectivity. To address these issues, we introduce HeNCler - a novel approach for Heterophilous Node Clustering. Our method begins by defining a weighted kernel singular value decomposition to create an asymmetric similarity graph, applicable to both directed and undirected graphs. We further establish that the dual problem of this formulation aligns with asymmetric kernel spectral clustering, interpreting learned graph similarities without relying on homophily. We demonstrate the ability to solve the primal problem directly, circumventing the computational difficulties of the dual approach. Experimental evidence confirms that HeNCler significantly enhances performance in node clustering tasks within heterophilous graph contexts.
Duality in Multi-View Restricted Kernel Machines
May 26, 2023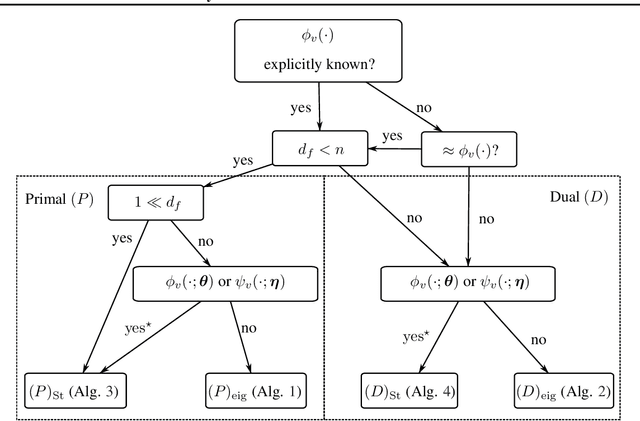
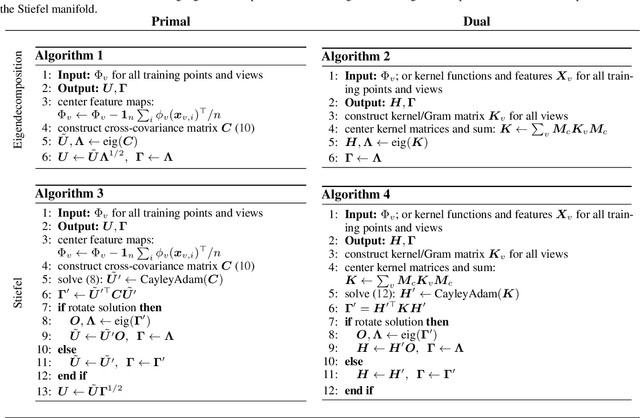
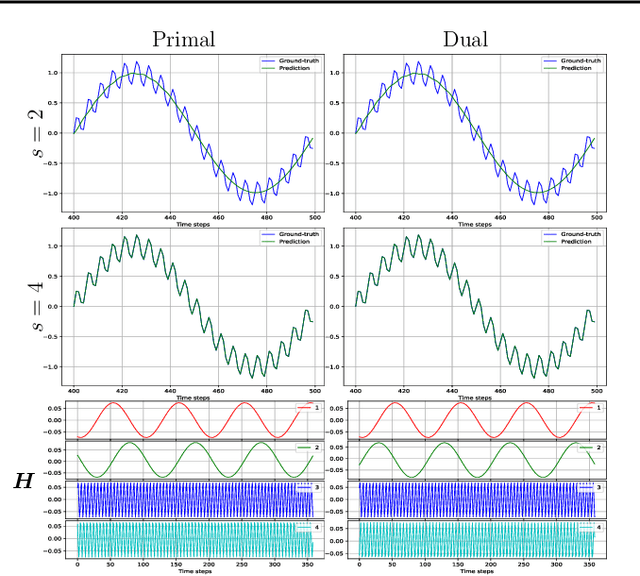
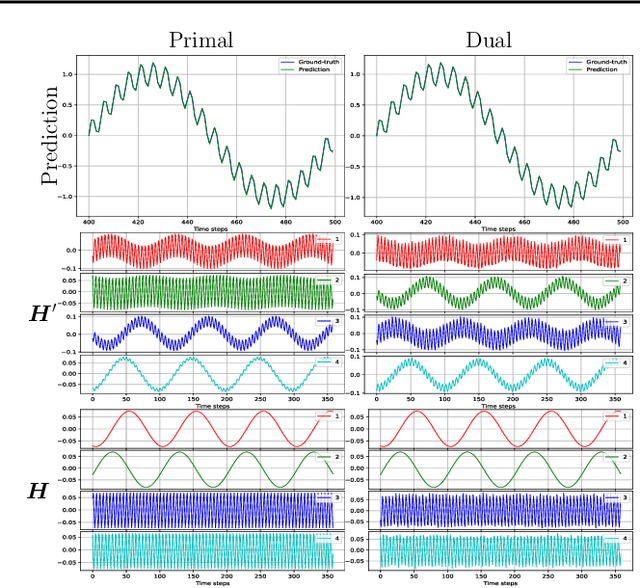
Abstract:We propose a unifying setting that combines existing restricted kernel machine methods into a single primal-dual multi-view framework for kernel principal component analysis in both supervised and unsupervised settings. We derive the primal and dual representations of the framework and relate different training and inference algorithms from a theoretical perspective. We show how to achieve full equivalence in primal and dual formulations by rescaling primal variables. Finally, we experimentally validate the equivalence and provide insight into the relationships between different methods on a number of time series data sets by recursively forecasting unseen test data and visualizing the learned features.
Semi-Supervised Classification with Graph Convolutional Kernel Machines
Jan 31, 2023Abstract:We present a deep Graph Convolutional Kernel Machine (GCKM) for semi-supervised node classification in graphs. First, we introduce an unsupervised kernel machine propagating the node features in a one-hop neighbourhood. Then, we specify a semi-supervised classification kernel machine through the lens of the Fenchel-Young inequality. The deep graph convolutional kernel machine is obtained by stacking multiple shallow kernel machines. After showing that unsupervised and semi-supervised layer corresponds to an eigenvalue problem and a linear system on the aggregated node features, respectively, we derive an efficient end-to-end training algorithm in the dual variables. Numerical experiments demonstrate that our approach is competitive with state-of-the-art graph neural networks for homophilious and heterophilious benchmark datasets. Notably, GCKM achieves superior performance when very few labels are available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge