Duality in Multi-View Restricted Kernel Machines

We propose a unifying setting that combines existing restricted kernel machine methods into a single primal-dual multi-view framework for kernel principal component analysis in both supervised and unsupervised settings. We derive the primal and dual representations of the framework and relate different training and inference algorithms from a theoretical perspective. We show how to achieve full equivalence in primal and dual formulations by rescaling primal variables. Finally, we experimentally validate the equivalence and provide insight into the relationships between different methods on a number of time series data sets by recursively forecasting unseen test data and visualizing the learned features.

Multi-view Kernel PCA for Time series Forecasting

In this paper, we propose a kernel principal component analysis model for multi-variate time series forecasting, where the training and prediction schemes are derived from the multi-view formulation of Restricted Kernel Machines. The training problem is simply an eigenvalue decomposition of the summation of two kernel matrices corresponding to the views of the input and output data. When a linear kernel is used for the output view, it is shown that the forecasting equation takes the form of kernel ridge regression. When that kernel is non-linear, a pre-image problem has to be solved to forecast a point in the input space. We evaluate the model on several standard time series datasets, perform ablation studies, benchmark with closely related models and discuss its results.

Unsupervised Energy-based Out-of-distribution Detection using Stiefel-Restricted Kernel Machine

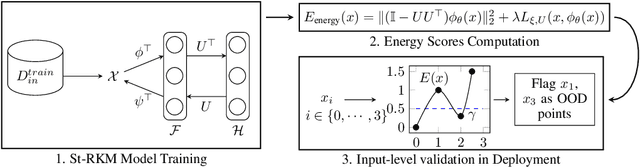
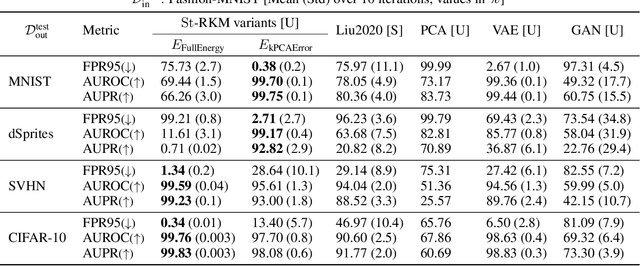
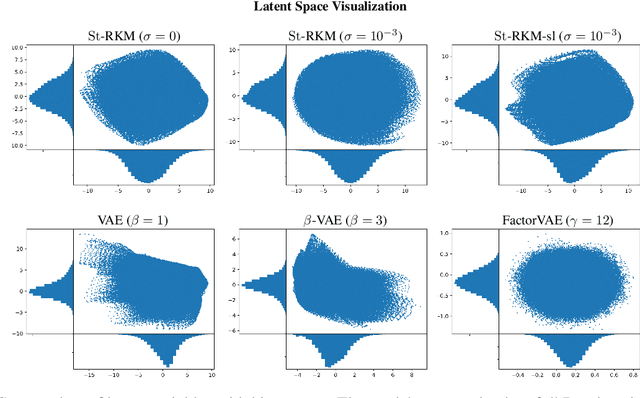
Detecting out-of-distribution (OOD) samples is an essential requirement for the deployment of machine learning systems in the real world. Until now, research on energy-based OOD detectors has focused on the softmax confidence score from a pre-trained neural network classifier with access to class labels. In contrast, we propose an unsupervised energy-based OOD detector leveraging the Stiefel-Restricted Kernel Machine (St-RKM). Training requires minimizing an objective function with an autoencoder loss term and the RKM energy where the interconnection matrix lies on the Stiefel manifold. Further, we outline multiple energy function definitions based on the RKM framework and discuss their utility. In the experiments on standard datasets, the proposed method improves over the existing energy-based OOD detectors and deep generative models. Through several ablation studies, we further illustrate the merit of each proposed energy function on the OOD detection performance.

Disentangled Representation Learning and Generation with Manifold Optimization

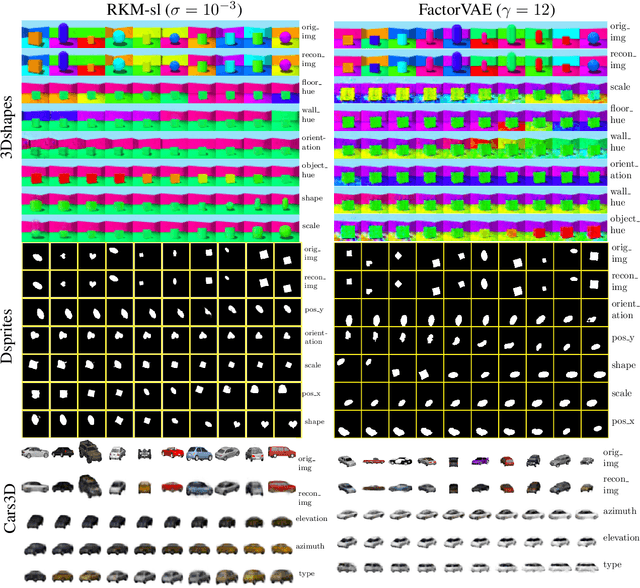
Disentanglement is an enjoyable property in representation learning which increases the interpretability of generative models such as Variational Auto-Encoders (VAE), Generative Adversarial Models and their many variants. In the context of latent space models, this work presents a representation learning framework that explicitly promotes disentanglement thanks to the combination of an auto-encoder with Principal Component Analysis (PCA) in latent space. The proposed objective is the sum of an auto-encoder error term along with a PCA reconstruction error in the feature space. This has an interpretation of a Restricted Kernel Machine with an interconnection matrix on the Stiefel manifold. The construction encourages a matching between the principal directions in latent space and the directions of orthogonal variation in data space. The training algorithm involves a stochastic optimization method on the Stiefel manifold, which increases only marginally the computing time compared to an analogous VAE. Our theoretical discussion and various experiments show that the proposed model improves over many VAE variants along with special emphasis on disentanglement learning.

Robust Generative Restricted Kernel Machines using Weighted Conjugate Feature Duality

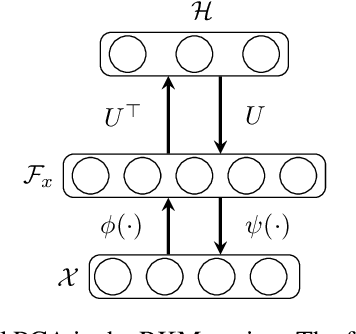
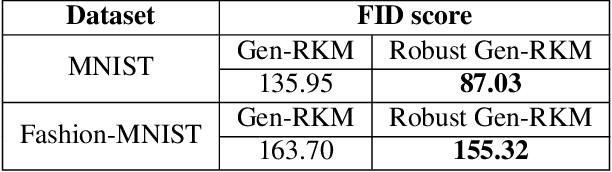
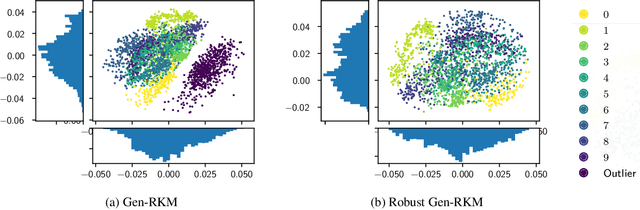
In the past decade, interest in generative models has grown tremendously. However, their training performance can be highly affected by contamination, where outliers are encoded in the representation of the model. This results in the generation of noisy data. In this paper, we introduce a weighted conjugate feature duality in the framework of Restricted Kernel Machines (RKMs). This formulation is used to fine-tune the latent space of generative RKMs using a weighting function based on the Minimum Covariance Determinant, which is a highly robust estimator of multivariate location and scatter. Experiments show that the weighted RKM is capable of generating clean images when contamination is present in the training data. We further show that the robust method also preserves uncorrelated feature learning through qualitative and quantitative experiments on standard datasets.

Generative Restricted Kernel Machines

We propose a novel method for estimating generative models based on the Restricted Kernel Machine (RKM) framework. This mechanism uses the shared representation of data from various sources where training only involves solving an eigenvalue problem. By defining an explicit feature map, we show that neural networks could be incorporated in the current framework. Experiments on various datasets demonstrate the potential of the model through qualitative evaluation of generated samples.