Accelerating Spectral Clustering under Fairness Constraints

Fairness of decision-making algorithms is an increasingly important issue. In this paper, we focus on spectral clustering with group fairness constraints, where every demographic group is represented in each cluster proportionally as in the general population. We present a new efficient method for fair spectral clustering (Fair SC) by casting the Fair SC problem within the difference of convex functions (DC) framework. To this end, we introduce a novel variable augmentation strategy and employ an alternating direction method of multipliers type of algorithm adapted to DC problems. We show that each associated subproblem can be solved efficiently, resulting in higher computational efficiency compared to prior work, which required a computationally expensive eigendecomposition. Numerical experiments demonstrate the effectiveness of our approach on both synthetic and real-world benchmarks, showing significant speedups in computation time over prior art, especially as the problem size grows. This work thus represents a considerable step forward towards the adoption of fair clustering in real-world applications.

Generative Kernel Spectral Clustering

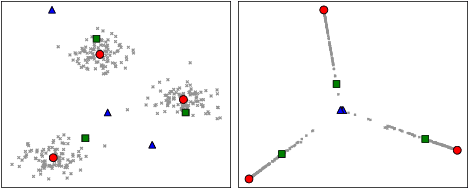
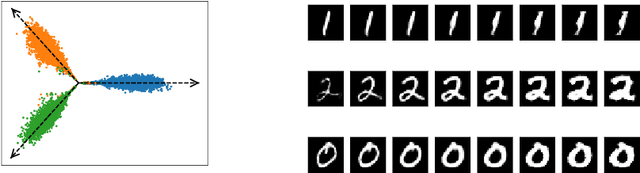
Modern clustering approaches often trade interpretability for performance, particularly in deep learning-based methods. We present Generative Kernel Spectral Clustering (GenKSC), a novel model combining kernel spectral clustering with generative modeling to produce both well-defined clusters and interpretable representations. By augmenting weighted variance maximization with reconstruction and clustering losses, our model creates an explorable latent space where cluster characteristics can be visualized through traversals along cluster directions. Results on MNIST and FashionMNIST datasets demonstrate the model's ability to learn meaningful cluster representations.

Learning in Feature Spaces via Coupled Covariances: Asymmetric Kernel SVD and Nyström method

In contrast with Mercer kernel-based approaches as used e.g., in Kernel Principal Component Analysis (KPCA), it was previously shown that Singular Value Decomposition (SVD) inherently relates to asymmetric kernels and Asymmetric Kernel Singular Value Decomposition (KSVD) has been proposed. However, the existing formulation to KSVD cannot work with infinite-dimensional feature mappings, the variational objective can be unbounded, and needs further numerical evaluation and exploration towards machine learning. In this work, i) we introduce a new asymmetric learning paradigm based on coupled covariance eigenproblem (CCE) through covariance operators, allowing infinite-dimensional feature maps. The solution to CCE is ultimately obtained from the SVD of the induced asymmetric kernel matrix, providing links to KSVD. ii) Starting from the integral equations corresponding to a pair of coupled adjoint eigenfunctions, we formalize the asymmetric Nystr\"om method through a finite sample approximation to speed up training. iii) We provide the first empirical evaluations verifying the practical utility and benefits of KSVD and compare with methods resorting to symmetrization or linear SVD across multiple tasks.

Learning Analysis of Kernel Ridgeless Regression with Asymmetric Kernel Learning

Ridgeless regression has garnered attention among researchers, particularly in light of the ``Benign Overfitting'' phenomenon, where models interpolating noisy samples demonstrate robust generalization. However, kernel ridgeless regression does not always perform well due to the lack of flexibility. This paper enhances kernel ridgeless regression with Locally-Adaptive-Bandwidths (LAB) RBF kernels, incorporating kernel learning techniques to improve performance in both experiments and theory. For the first time, we demonstrate that functions learned from LAB RBF kernels belong to an integral space of Reproducible Kernel Hilbert Spaces (RKHSs). Despite the absence of explicit regularization in the proposed model, its optimization is equivalent to solving an $\ell_0$-regularized problem in the integral space of RKHSs, elucidating the origin of its generalization ability. Taking an approximation analysis viewpoint, we introduce an $l_q$-norm analysis technique (with $0<q<1$) to derive the learning rate for the proposed model under mild conditions. This result deepens our theoretical understanding, explaining that our algorithm's robust approximation ability arises from the large capacity of the integral space of RKHSs, while its generalization ability is ensured by sparsity, controlled by the number of support vectors. Experimental results on both synthetic and real datasets validate our theoretical conclusions.

HeNCler: Node Clustering in Heterophilous Graphs through Learned Asymmetric Similarity

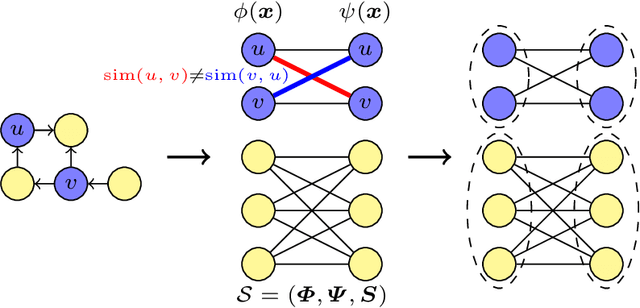
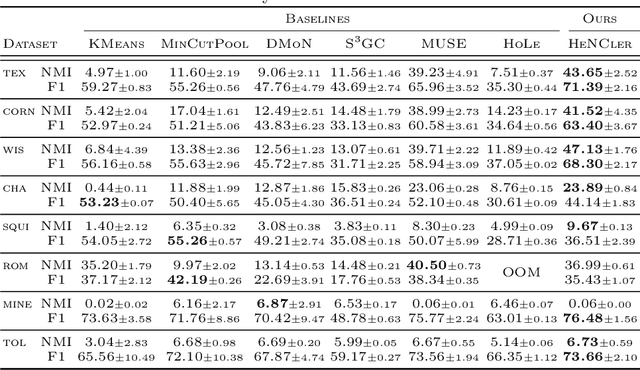
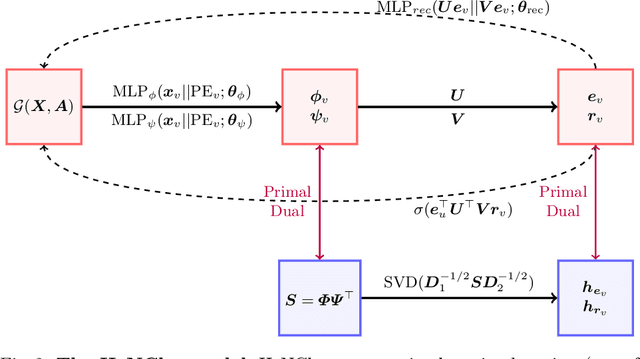
Clustering nodes in heterophilous graphs presents unique challenges due to the asymmetric relationships often overlooked by traditional methods, which moreover assume that good clustering corresponds to high intra-cluster and low inter-cluster connectivity. To address these issues, we introduce HeNCler - a novel approach for Heterophilous Node Clustering. Our method begins by defining a weighted kernel singular value decomposition to create an asymmetric similarity graph, applicable to both directed and undirected graphs. We further establish that the dual problem of this formulation aligns with asymmetric kernel spectral clustering, interpreting learned graph similarities without relying on homophily. We demonstrate the ability to solve the primal problem directly, circumventing the computational difficulties of the dual approach. Experimental evidence confirms that HeNCler significantly enhances performance in node clustering tasks within heterophilous graph contexts.

Sparsity via Sparse Group $k$-max Regularization

For the linear inverse problem with sparsity constraints, the $l_0$ regularized problem is NP-hard, and existing approaches either utilize greedy algorithms to find almost-optimal solutions or to approximate the $l_0$ regularization with its convex counterparts. In this paper, we propose a novel and concise regularization, namely the sparse group $k$-max regularization, which can not only simultaneously enhance the group-wise and in-group sparsity, but also casts no additional restraints on the magnitude of variables in each group, which is especially important for variables at different scales, so that it approximate the $l_0$ norm more closely. We also establish an iterative soft thresholding algorithm with local optimality conditions and complexity analysis provided. Through numerical experiments on both synthetic and real-world datasets, we verify the effectiveness and flexibility of the proposed method.

Self-Attention through Kernel-Eigen Pair Sparse Variational Gaussian Processes

While the great capability of Transformers significantly boosts prediction accuracy, it could also yield overconfident predictions and require calibrated uncertainty estimation, which can be commonly tackled by Gaussian processes (GPs). Existing works apply GPs with symmetric kernels under variational inference to the attention kernel; however, omitting the fact that attention kernels are in essence asymmetric. Moreover, the complexity of deriving the GP posteriors remains high for large-scale data. In this work, we propose Kernel-Eigen Pair Sparse Variational Gaussian Processes (KEP-SVGP) for building uncertainty-aware self-attention where the asymmetry of attention kernels is tackled by Kernel SVD (KSVD) and a reduced complexity is acquired. Through KEP-SVGP, i) the SVGP pair induced by the two sets of singular vectors from KSVD w.r.t. the attention kernel fully characterizes the asymmetry; ii) using only a small set of adjoint eigenfunctions from KSVD, the derivation of SVGP posteriors can be based on the inversion of a diagonal matrix containing singular values, contributing to a reduction in time complexity; iii) an evidence lower bound is derived so that variational parameters can be optimized towards this objective. Experiments verify our excellent performances and efficiency on in-distribution, distribution-shift and out-of-distribution benchmarks.

Can overfitted deep neural networks in adversarial training generalize? -- An approximation viewpoint

Adversarial training is a widely used method to improve the robustness of deep neural networks (DNNs) over adversarial perturbations. However, it is empirically observed that adversarial training on over-parameterized networks often suffers from the \textit{robust overfitting}: it can achieve almost zero adversarial training error while the robust generalization performance is not promising. In this paper, we provide a theoretical understanding of the question of whether overfitted DNNs in adversarial training can generalize from an approximation viewpoint. Specifically, our main results are summarized into three folds: i) For classification, we prove by construction the existence of infinitely many adversarial training classifiers on over-parameterized DNNs that obtain arbitrarily small adversarial training error (overfitting), whereas achieving good robust generalization error under certain conditions concerning the data quality, well separated, and perturbation level. ii) Linear over-parameterization (meaning that the number of parameters is only slightly larger than the sample size) is enough to ensure such existence if the target function is smooth enough. iii) For regression, our results demonstrate that there also exist infinitely many overfitted DNNs with linear over-parameterization in adversarial training that can achieve almost optimal rates of convergence for the standard generalization error. Overall, our analysis points out that robust overfitting can be avoided but the required model capacity will depend on the smoothness of the target function, while a robust generalization gap is inevitable. We hope our analysis will give a better understanding of the mathematical foundations of robustness in DNNs from an approximation view.

Nonlinear functional regression by functional deep neural network with kernel embedding

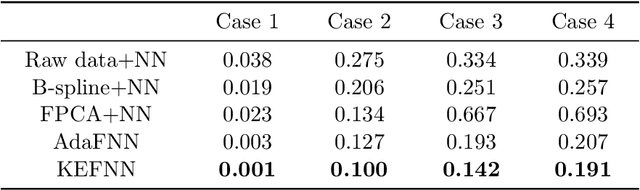
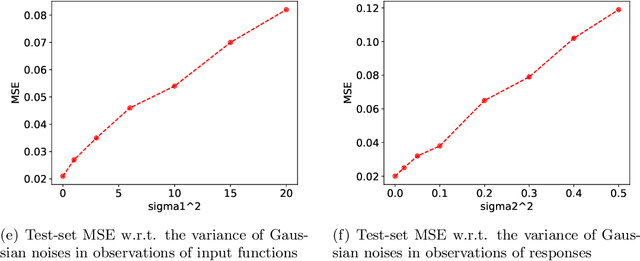
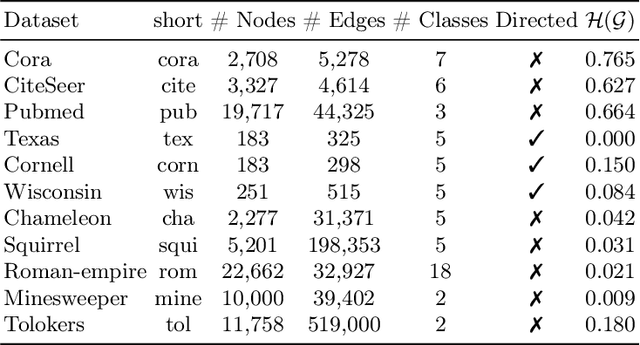
With the rapid development of deep learning in various fields of science and technology, such as speech recognition, image classification, and natural language processing, recently it is also widely applied in the functional data analysis (FDA) with some empirical success. However, due to the infinite dimensional input, we need a powerful dimension reduction method for functional learning tasks, especially for the nonlinear functional regression. In this paper, based on the idea of smooth kernel integral transformation, we propose a functional deep neural network with an efficient and fully data-dependent dimension reduction method. The architecture of our functional net consists of a kernel embedding step: an integral transformation with a data-dependent smooth kernel; a projection step: a dimension reduction by projection with eigenfunction basis based on the embedding kernel; and finally an expressive deep ReLU neural network for the prediction. The utilization of smooth kernel embedding enables our functional net to be discretization invariant, efficient, and robust to noisy observations, capable of utilizing information in both input functions and responses data, and have a low requirement on the number of discrete points for an unimpaired generalization performance. We conduct theoretical analysis including approximation error and generalization error analysis, and numerical simulations to verify these advantages of our functional net.

Enhancing Kernel Flexibility via Learning Asymmetric Locally-Adaptive Kernels

The lack of sufficient flexibility is the key bottleneck of kernel-based learning that relies on manually designed, pre-given, and non-trainable kernels. To enhance kernel flexibility, this paper introduces the concept of Locally-Adaptive-Bandwidths (LAB) as trainable parameters to enhance the Radial Basis Function (RBF) kernel, giving rise to the LAB RBF kernel. The parameters in LAB RBF kernels are data-dependent, and its number can increase with the dataset, allowing for better adaptation to diverse data patterns and enhancing the flexibility of the learned function. This newfound flexibility also brings challenges, particularly with regards to asymmetry and the need for an efficient learning algorithm. To address these challenges, this paper for the first time establishes an asymmetric kernel ridge regression framework and introduces an iterative kernel learning algorithm. This novel approach not only reduces the demand for extensive support data but also significantly improves generalization by training bandwidths on the available training data. Experimental results on real datasets underscore the remarkable performance of the proposed algorithm, showcasing its superior capability in handling large-scale datasets compared to Nystr\"om approximation-based algorithms. Moreover, it demonstrates a significant improvement in regression accuracy over existing kernel-based learning methods and even surpasses residual neural networks.