Modeling Output-Level Task Relatedness in Multi-Task Learning with Feedback Mechanism

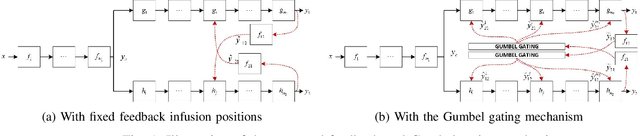
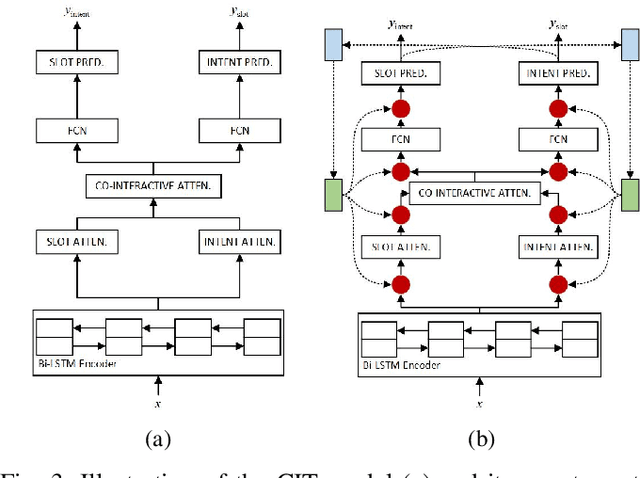
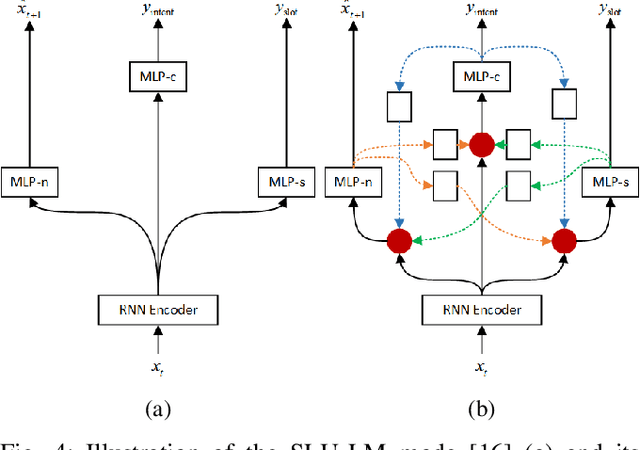
Multi-task learning (MTL) is a paradigm that simultaneously learns multiple tasks by sharing information at different levels, enhancing the performance of each individual task. While previous research has primarily focused on feature-level or parameter-level task relatedness, and proposed various model architectures and learning algorithms to improve learning performance, we aim to explore output-level task relatedness. This approach introduces a posteriori information into the model, considering that different tasks may produce correlated outputs with mutual influences. We achieve this by incorporating a feedback mechanism into MTL models, where the output of one task serves as a hidden feature for another task, thereby transforming a static MTL model into a dynamic one. To ensure the training process converges, we introduce a convergence loss that measures the trend of a task's outputs during each iteration. Additionally, we propose a Gumbel gating mechanism to determine the optimal projection of feedback signals. We validate the effectiveness of our method and evaluate its performance through experiments conducted on several baseline models in spoken language understanding.

Multi-Objective Trajectory Planning with Dual-Encoder

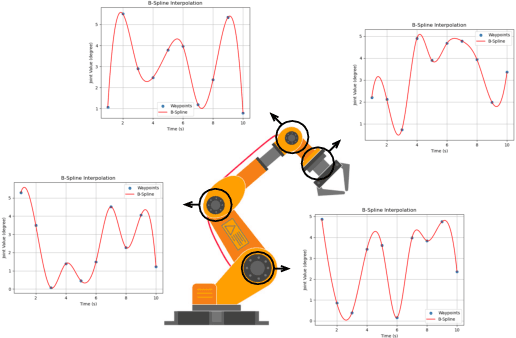
Time-jerk optimal trajectory planning is crucial in advancing robotic arms' performance in dynamic tasks. Traditional methods rely on solving complex nonlinear programming problems, bringing significant delays in generating optimized trajectories. In this paper, we propose a two-stage approach to accelerate time-jerk optimal trajectory planning. Firstly, we introduce a dual-encoder based transformer model to establish a good preliminary trajectory. This trajectory is subsequently refined through sequential quadratic programming to improve its optimality and robustness. Our approach outperforms the state-of-the-art by up to 79.72\% in reducing trajectory planning time. Compared with existing methods, our method shrinks the optimality gap with the objective function value decreasing by up to 29.9\%.

Sparsity via Sparse Group $k$-max Regularization

For the linear inverse problem with sparsity constraints, the $l_0$ regularized problem is NP-hard, and existing approaches either utilize greedy algorithms to find almost-optimal solutions or to approximate the $l_0$ regularization with its convex counterparts. In this paper, we propose a novel and concise regularization, namely the sparse group $k$-max regularization, which can not only simultaneously enhance the group-wise and in-group sparsity, but also casts no additional restraints on the magnitude of variables in each group, which is especially important for variables at different scales, so that it approximate the $l_0$ norm more closely. We also establish an iterative soft thresholding algorithm with local optimality conditions and complexity analysis provided. Through numerical experiments on both synthetic and real-world datasets, we verify the effectiveness and flexibility of the proposed method.

Piecewise Linear Neural Networks and Deep Learning

As a powerful modelling method, PieceWise Linear Neural Networks (PWLNNs) have proven successful in various fields, most recently in deep learning. To apply PWLNN methods, both the representation and the learning have long been studied. In 1977, the canonical representation pioneered the works of shallow PWLNNs learned by incremental designs, but the applications to large-scale data were prohibited. In 2010, the Rectified Linear Unit (ReLU) advocated the prevalence of PWLNNs in deep learning. Ever since, PWLNNs have been successfully applied to extensive tasks and achieved advantageous performances. In this Primer, we systematically introduce the methodology of PWLNNs by grouping the works into shallow and deep networks. Firstly, different PWLNN representation models are constructed with elaborated examples. With PWLNNs, the evolution of learning algorithms for data is presented and fundamental theoretical analysis follows up for in-depth understandings. Then, representative applications are introduced together with discussions and outlooks.

Efficient hinging hyperplanes neural network and its application in nonlinear system identification

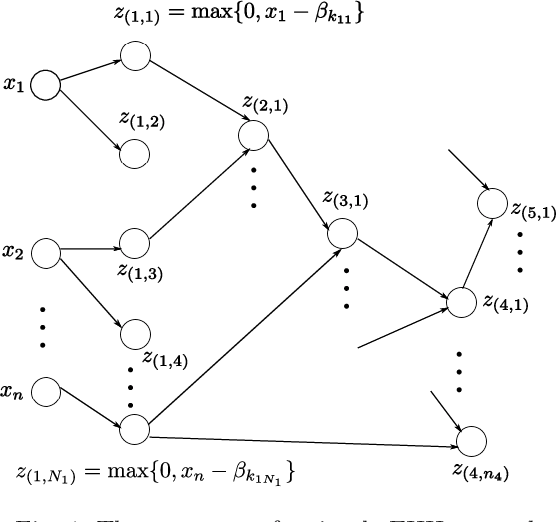
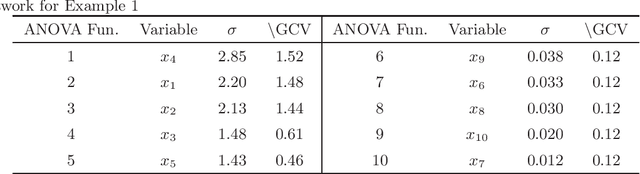
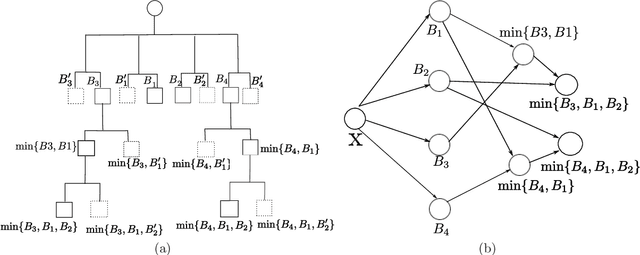
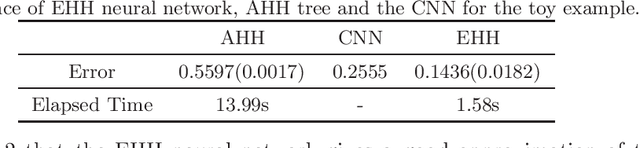
In this paper, the efficient hinging hyperplanes (EHH) neural network is proposed based on the model of hinging hyperplanes (HH). The EHH neural network is a distributed representation, the training of which involves solving several convex optimization problems and is fast. It is proved that for every EHH neural network, there is an equivalent adaptive hinging hyperplanes (AHH) tree, which was also proposed based on the model of HH and find good applications in system identification. The construction of the EHH neural network includes 2 stages. First the initial structure of the EHH neural network is randomly determined and the Lasso regression is used to choose the appropriate network. To alleviate the impact of randomness, secondly, the stacking strategy is employed to formulate a more general network structure. Different from other neural networks, the EHH neural network has interpretability ability, which can be easily obtained through its ANOVA decomposition (or interaction matrix). The interpretability can then be used as a suggestion for input variable selection. The EHH neural network is applied in nonlinear system identification, the simulation results show that the regression vector selected is reasonable and the identification speed is fast, while at the same time, the simulation accuracy is satisfactory.