Subgraph Aggregation for Out-of-Distribution Generalization on Graphs

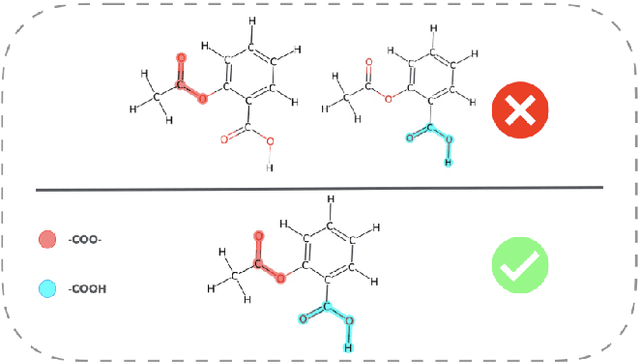
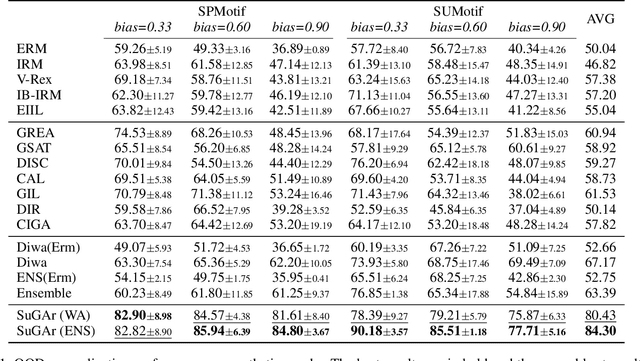
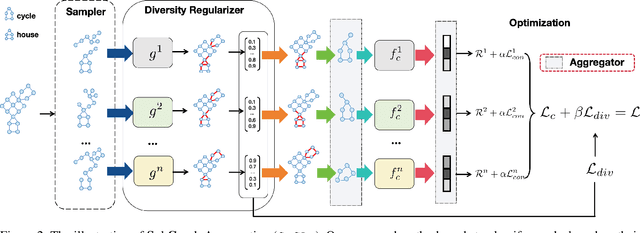
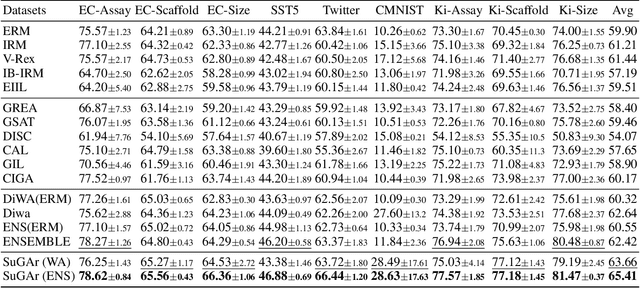
Out-of-distribution (OOD) generalization in Graph Neural Networks (GNNs) has gained significant attention due to its critical importance in graph-based predictions in real-world scenarios. Existing methods primarily focus on extracting a single causal subgraph from the input graph to achieve generalizable predictions. However, relying on a single subgraph can lead to susceptibility to spurious correlations and is insufficient for learning invariant patterns behind graph data. Moreover, in many real-world applications, such as molecular property prediction, multiple critical subgraphs may influence the target label property. To address these challenges, we propose a novel framework, SubGraph Aggregation (SuGAr), designed to learn a diverse set of subgraphs that are crucial for OOD generalization on graphs. Specifically, SuGAr employs a tailored subgraph sampler and diversity regularizer to extract a diverse set of invariant subgraphs. These invariant subgraphs are then aggregated by averaging their representations, which enriches the subgraph signals and enhances coverage of the underlying causal structures, thereby improving OOD generalization. Extensive experiments on both synthetic and real-world datasets demonstrate that \ours outperforms state-of-the-art methods, achieving up to a 24% improvement in OOD generalization on graphs. To the best of our knowledge, this is the first work to study graph OOD generalization by learning multiple invariant subgraphs.

Piecewise Linear Neural Networks and Deep Learning

As a powerful modelling method, PieceWise Linear Neural Networks (PWLNNs) have proven successful in various fields, most recently in deep learning. To apply PWLNN methods, both the representation and the learning have long been studied. In 1977, the canonical representation pioneered the works of shallow PWLNNs learned by incremental designs, but the applications to large-scale data were prohibited. In 2010, the Rectified Linear Unit (ReLU) advocated the prevalence of PWLNNs in deep learning. Ever since, PWLNNs have been successfully applied to extensive tasks and achieved advantageous performances. In this Primer, we systematically introduce the methodology of PWLNNs by grouping the works into shallow and deep networks. Firstly, different PWLNN representation models are constructed with elaborated examples. With PWLNNs, the evolution of learning algorithms for data is presented and fundamental theoretical analysis follows up for in-depth understandings. Then, representative applications are introduced together with discussions and outlooks.

Efficient hinging hyperplanes neural network and its application in nonlinear system identification

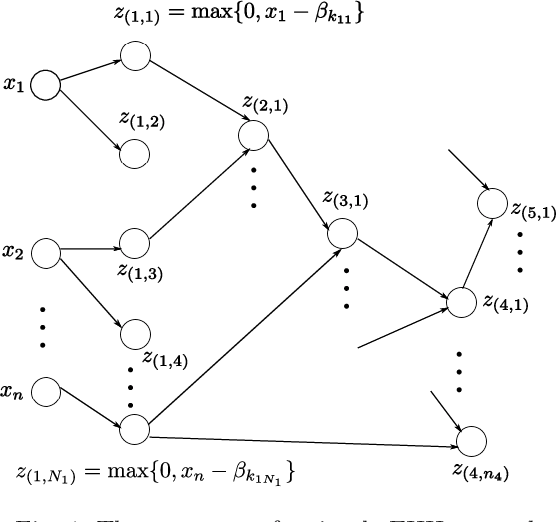
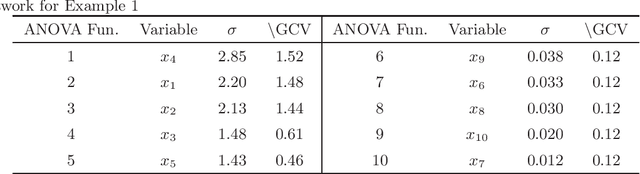
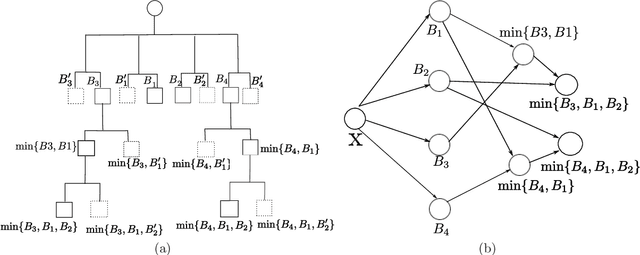
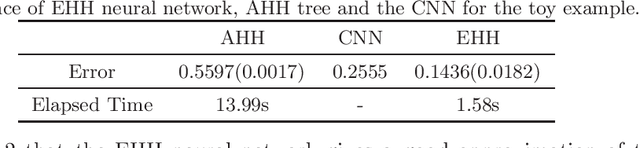
In this paper, the efficient hinging hyperplanes (EHH) neural network is proposed based on the model of hinging hyperplanes (HH). The EHH neural network is a distributed representation, the training of which involves solving several convex optimization problems and is fast. It is proved that for every EHH neural network, there is an equivalent adaptive hinging hyperplanes (AHH) tree, which was also proposed based on the model of HH and find good applications in system identification. The construction of the EHH neural network includes 2 stages. First the initial structure of the EHH neural network is randomly determined and the Lasso regression is used to choose the appropriate network. To alleviate the impact of randomness, secondly, the stacking strategy is employed to formulate a more general network structure. Different from other neural networks, the EHH neural network has interpretability ability, which can be easily obtained through its ANOVA decomposition (or interaction matrix). The interpretability can then be used as a suggestion for input variable selection. The EHH neural network is applied in nonlinear system identification, the simulation results show that the regression vector selected is reasonable and the identification speed is fast, while at the same time, the simulation accuracy is satisfactory.